Dalam dunia matematika, Faktor Persekutuan Terbesar (FPB) memegang peranan penting dalam menemukan nilai umum terbesar yang membagi beberapa bilangan bulat secara merata. FPB memiliki aplikasi yang luas dalam berbagai bidang, mulai dari teori bilangan hingga desain teknik.

Artikel ini akan mengulas secara mendalam konsep FPB, mengeksplorasi algoritma untuk menghitungnya, dan menguraikan penerapannya yang praktis. Melalui eksplorasi ini, kita akan memperoleh pemahaman yang komprehensif tentang peran penting FPB dalam matematika dan kehidupan sehari-hari.

Pengertian Faktor Persekutuan Terbesar (FPB)

Faktor Persekutuan Terbesar (FPB) dari dua bilangan atau lebih adalah bilangan bulat positif terbesar yang merupakan faktor dari semua bilangan tersebut.

Sebagai contoh, FPB dari 12 dan 18 adalah 6, karena 6 adalah faktor dari 12 dan 18, dan merupakan bilangan bulat positif terbesar yang memiliki sifat tersebut.

Metode Mencari FPB

Ada beberapa metode untuk mencari FPB, di antaranya:

1. Metode Faktorisasi Prima: Faktorisasi semua bilangan yang terlibat menjadi faktor-faktor primanya, kemudian ambil faktor-faktor prima yang sama dan kalikan pangkat terkecilnya.
2. Metode Pembagian Berulang: Bagi bilangan yang lebih besar dengan bilangan yang lebih kecil. Ulangi proses ini dengan hasil bagi dan pembagi sebelumnya sampai pembaginya menjadi 0. FPB adalah pembagi terakhir yang tidak sama dengan 0.
3. Metode Algoritma Euklides: Ini adalah algoritma efisien yang digunakan untuk mencari FPB dari dua bilangan. Algoritma ini menggunakan operasi pembagian berulang untuk mengurangi bilangan yang lebih besar dengan bilangan yang lebih kecil sampai bilangan yang lebih kecil menjadi 0. FPB adalah bilangan terakhir yang dibagi.

Mencari FPB Menggunakan Algoritma Euklides

Algoritma Euklides adalah metode efisien untuk menemukan faktor persekutuan terbesar (FPB) dari dua bilangan. Algoritma ini bekerja dengan berulang kali membagi bilangan yang lebih besar dengan bilangan yang lebih kecil dan menggunakan sisa pembagian untuk mengulangi proses tersebut hingga sisa menjadi nol.

Langkah-langkah Algoritma Euklides

1. Bagilah bilangan yang lebih besar dengan bilangan yang lebih kecil.
2. Ambil sisa dari pembagian tersebut.
3. Bagi bilangan yang lebih kecil dengan sisa dari pembagian sebelumnya.
4. Ulangi langkah 2 dan 3 hingga sisa menjadi nol.
5. Bilangan terakhir yang bukan nol sebelum sisa menjadi nol adalah FPB dari kedua bilangan tersebut.

Contoh Langkah Demi Langkah

Misalkan kita ingin mencari FPB dari 54 dan 72.

1. 72 ÷ 54 = 1, sisa 18
2. 54 ÷ 18 = 3, sisa 0

Oleh karena itu, FPB dari 54 dan 72 adalah 18.

Metode Faktor Prima

Metode faktor prima adalah cara untuk mencari faktor persekutuan terbesar (FPB) dari dua bilangan atau lebih dengan menguraikannya menjadi faktor-faktor prima.

Untuk menggunakan metode ini, kita perlu mengikuti langkah-langkah berikut:

Menguraikan Bilangan Menjadi Faktor Prima

1. Bagi bilangan yang diberikan dengan bilangan prima terkecil yang habis membaginya.
2. Teruskan pembagian dengan bilangan prima terkecil berikutnya yang habis membagi hasil bagi.
3. Ulangi langkah 2 sampai hasil bagi tidak dapat dibagi lagi dengan bilangan prima.
4. Faktorisasi bilangan menjadi perkalian faktor-faktor prima yang diperoleh.

Mencari FPB

1. Tulis faktorisasi prima dari semua bilangan yang diberikan.
2. Pilih faktor-faktor prima yang sama dari setiap faktorisasi.
3. Kalikan faktor-faktor prima yang dipilih bersama untuk mendapatkan FPB.

Contoh

Misalkan kita ingin mencari FPB dari 54, 72, dan 90. Faktorisasi prima dari bilangan-bilangan tersebut adalah:

• 54 = 2 × 3 × 3 × 3
• 72 = 2 × 2 × 2 × 3 × 3
• 90 = 2 × 3 × 3 × 5

Faktor-faktor prima yang sama adalah 2 dan 3. Oleh karena itu, FPB dari 54, 72, dan 90 adalah 2 × 3 = 6.

Mencari FPB dari Banyak Bilangan

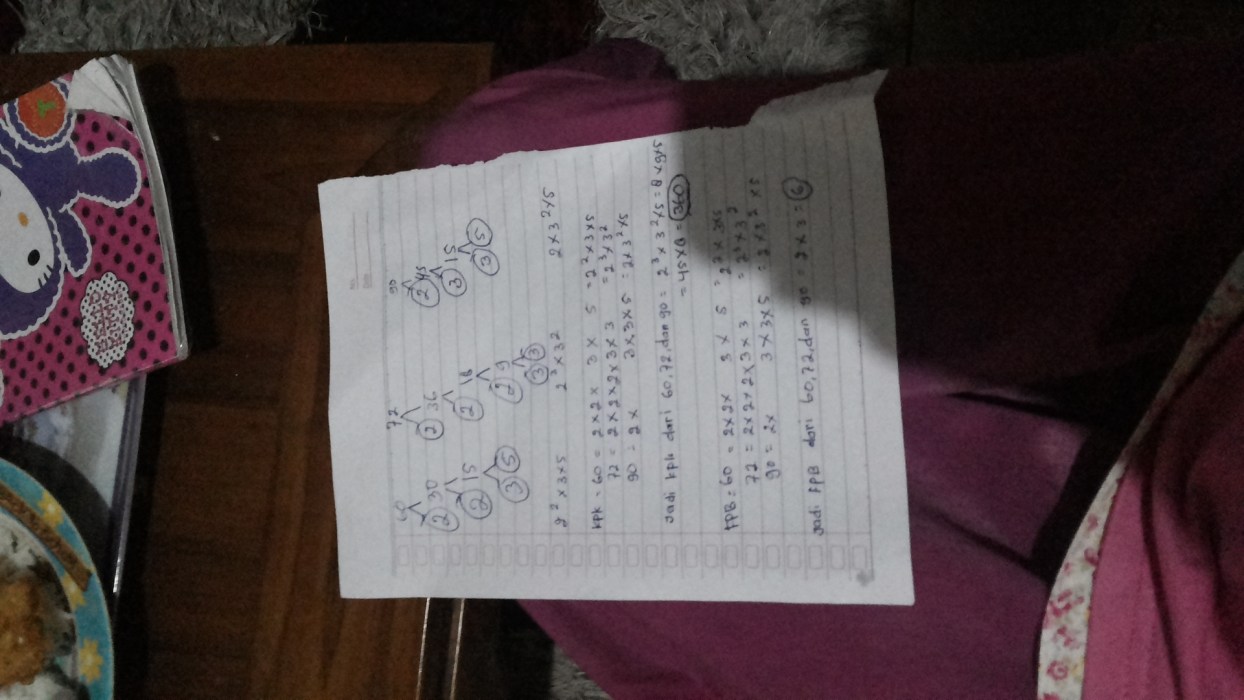
FPB (Faktor Persekutuan Terbesar) dari suatu himpunan bilangan adalah bilangan terbesar yang merupakan faktor dari semua bilangan dalam himpunan tersebut.

Untuk mencari FPB dari lebih dari dua bilangan, dapat digunakan metode berikut:

Mencari FPB dari Tiga atau Lebih Bilangan

• Cari FPB dari dua bilangan pertama dalam himpunan.
• Cari FPB dari FPB tersebut dan bilangan ketiga.
• Ulangi langkah kedua hingga semua bilangan dalam himpunan dipertimbangkan.

Berikut adalah tabel yang menunjukkan proses mencari FPB dari tiga atau lebih bilangan:

Bilangan	FPB Sementara
54, 72, 90	18
18, 90	18
18, 72	18

Jadi, FPB dari 54, 72, dan 90 adalah 18.

Aplikasi FPB dalam Kehidupan Sehari-hari

Faktor Persekutuan Terbesar (FPB) memiliki berbagai aplikasi praktis dalam kehidupan sehari-hari. FPB digunakan dalam perhitungan waktu, desain, dan situasi lain yang membutuhkan penentuan pembagi umum terbesar antara dua atau lebih bilangan.

Perhitungan Waktu

Dalam perhitungan waktu, FPB digunakan untuk menentukan periode waktu terpendek yang sama dengan beberapa periode waktu lainnya. Misalnya, FPB dari 12 dan 18 adalah 6, yang menunjukkan bahwa jam dengan 12 pembagian dan jam dengan 18 pembagian akan bertemu kembali pada posisi yang sama setiap 6 jam.

Desain

Dalam desain, FPB digunakan untuk menentukan skala dan proporsi objek yang harmonis. Misalnya, rasio emas, yang sering dianggap estetis, adalah sekitar 1,618, yang merupakan FPB dari 2 dan 3.

Situasi Umum

Selain itu, FPB digunakan dalam berbagai situasi umum, seperti:

• Menyederhanakan pecahan
• Menyelesaikan persamaan Diophantine
• Membagi tugas secara adil di antara beberapa orang
• Menentukan ukuran terbesar yang dapat dibagi rata menjadi beberapa bagian

Kasus Khusus dan Batasan

Dalam mencari FPB, terdapat beberapa kasus khusus dan batasan yang perlu dipertimbangkan.

Bilangan Saling Prima

Bilangan saling prima adalah bilangan yang hanya memiliki faktor pembagi 1 dan bilangan itu sendiri. Dalam hal ini, FPB dari bilangan saling prima adalah 1. Misalnya, FPB dari 11 dan 13 adalah 1.

Batasan Metode

Metode yang umum digunakan untuk mencari FPB, seperti metode faktorisasi prima dan algoritma Euklides, memiliki batasan tertentu. Metode faktorisasi prima hanya efektif untuk bilangan kecil, sedangkan algoritma Euklides dapat menjadi tidak efisien untuk bilangan yang sangat besar.

Terakhir

Dengan memahami FPB, kita memperoleh alat yang ampuh untuk memecahkan berbagai masalah matematika dan aplikasi dunia nyata. Dari menentukan waktu terpendek yang umum hingga mendesain pola simetris, FPB membuktikan nilainya sebagai konsep fundamental dalam dunia bilangan.

Tanya Jawab (Q&A)

Apa saja langkah-langkah algoritma Euklides untuk mencari FPB?

Algoritma Euklides menggunakan pembagian berulang untuk mencari FPB. Langkah-langkahnya adalah:

1. Bagi bilangan yang lebih besar dengan bilangan yang lebih kecil.
2. Ambil sisa dari pembagian tersebut.
3. Ulangi langkah 1 dan 2 dengan bilangan yang lebih kecil dan sisa sebelumnya.
4. Ketika sisa menjadi 0, bilangan yang lebih kecil pada langkah sebelumnya adalah FPB.

Bagaimana cara mencari FPB dari lebih dari dua bilangan?

Untuk mencari FPB dari lebih dari dua bilangan, kita dapat menggunakan metode berikut:

1. Temukan FPB dari dua bilangan pertama.
2. Cari FPB dari hasil langkah 1 dan bilangan ketiga.
3. Ulangi langkah 2 hingga semua bilangan disertakan.

Apa saja aplikasi FPB dalam kehidupan sehari-hari?

FPB memiliki berbagai aplikasi, termasuk: