Dalam matematika, fungsi merupakan konsep fundamental yang digunakan untuk memodelkan hubungan antara dua variabel. Fungsi f ditentukan oleh adalah konsep penting yang mendefinisikan hubungan ini dengan jelas dan ringkas.

Fungsi f ditentukan oleh menetapkan nilai variabel dependen (output) untuk setiap nilai variabel independen (input) dalam domain tertentu. Konsep ini menjadi dasar berbagai jenis fungsi, operasi, dan sifat yang memainkan peran penting dalam berbagai bidang, termasuk sains, teknik, dan kehidupan sehari-hari.

Pengertian Fungsi

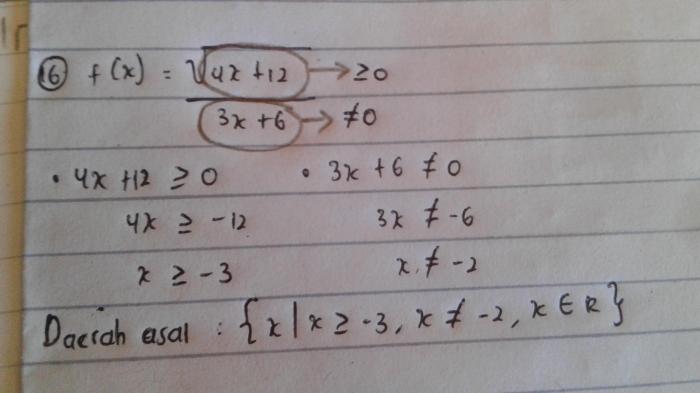
Dalam matematika, fungsi adalah relasi antara dua himpunan, di mana setiap elemen dari himpunan pertama dipetakan ke satu elemen unik dari himpunan kedua.

Dengan kata lain, fungsi adalah aturan yang menetapkan setiap masukan dari suatu himpunan (disebut domain) ke keluaran yang unik dari himpunan lain (disebut kodomain).

Contoh Fungsi Sederhana

Salah satu contoh sederhana dari fungsi adalah fungsi linear, yang didefinisikan sebagai berikut:

f(x) = mx + b

Dalam fungsi ini, x adalah variabel independen (input), m adalah kemiringan garis, dan b adalah titik potong y. Untuk setiap nilai x, fungsi ini menghasilkan keluaran f(x), yang merupakan titik pada garis dengan kemiringan m dan titik potong y b.

Penentuan Fungsi

Fungsi ditentukan oleh suatu hubungan antara dua himpunan, X dan Y, di mana setiap anggota himpunan X dipasangkan dengan tepat satu anggota himpunan Y.

Komponen utama dalam penentuan fungsi adalah:

Domain

Himpunan semua nilai masukan yang dapat diambil oleh fungsi.

Kodomain

Himpunan semua nilai keluaran yang dapat dihasilkan oleh fungsi.

Relasi

Aturan yang menentukan pasangan antara anggota domain dan kodomain.

Jenis-Jenis Fungsi

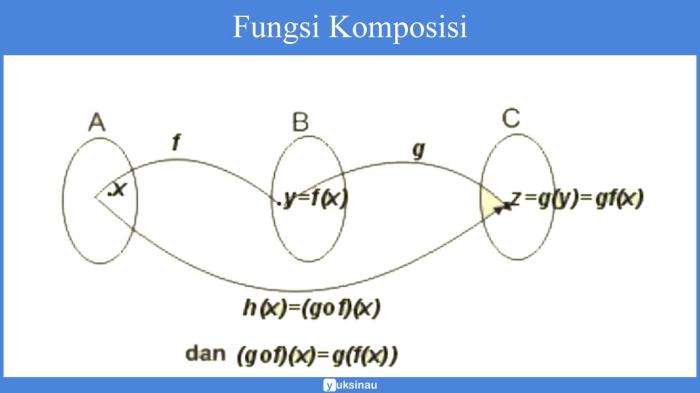
Fungsi merupakan hubungan antara satu himpunan (domain) dengan himpunan lain (kodomain) yang memasangkan setiap anggota domain dengan tepat satu anggota kodomain. Fungsi memiliki beberapa jenis, antara lain:

Fungsi Linear

• Rumus: f(x) = mx + b
• Grafik: Garis lurus
• Contoh: f(x) = 2x + 3

Fungsi Kuadrat

• Rumus: f(x) = ax² + bx + c
• Grafik: Parabola
• Contoh: f(x) = x²
  – 2x + 1

Fungsi Eksponensial

• Rumus: f(x) = a^x
• Grafik: Kurva naik atau turun
• Contoh: f(x) = 2^x

Fungsi Logaritma

• Rumus: f(x) = log_ax
• Grafik: Kurva naik atau turun
• Contoh: f(x) = log₂x

Fungsi Trigonometri

• Rumus: f(x) = sin x, cos x, tan x, dll.
• Grafik: Kurva periodik
• Contoh: f(x) = sin x

Operasi pada Fungsi

Operasi pada fungsi melibatkan penerapan operasi matematika dasar seperti penjumlahan, pengurangan, perkalian, dan pembagian pada dua atau lebih fungsi.

Penjumlahan dan Pengurangan Fungsi

• Penjumlahan fungsi: (f + g)(x) = f(x) + g(x)
• Pengurangan fungsi: (f
  – g)(x) = f(x)
  – g(x)

Contoh: Jika f(x) = x^2 dan g(x) = x + 1, maka (f + g)(x) = x^2 + x + 1 dan (f – g)(x) = x^2 – x – 1.

Perkalian dan Pembagian Fungsi

• Perkalian fungsi: (f
  – g)(x) = f(x)
  – g(x)
• Pembagian fungsi: (f / g)(x) = f(x) / g(x), dengan g(x) ≠ 0

Contoh: Jika f(x) = 2x dan g(x) = x – 1, maka (f – g)(x) = 2x(x – 1) = 2x^2 – 2x dan (f / g)(x) = 2x / (x – 1), x ≠ 1.

Sifat-Sifat Fungsi

Fungsi memiliki sifat-sifat tertentu yang dapat diklasifikasikan berdasarkan hubungan antara domain dan kodomainnya.

Injeksi

Fungsi f: A → B dikatakan injeksi (satu-satu) jika untuk setiap a ₁ , a ₂ ∈ A, jika f(a ₁ ) = f(a ₂ ), maka a ₁ = a ₂ . Dengan kata lain, fungsi injeksi memetakan elemen yang berbeda dari domain ke elemen yang berbeda dari kodomain.

Contoh:

• f(x) = x², x ∈ R
• f(x) = sin(x), x ∈ R

Surjeksi

Fungsi f: A → B dikatakan surjeksi (banyak-satu) jika untuk setiap b ∈ B, terdapat setidaknya satu a ∈ A sehingga f(a) = b. Dengan kata lain, fungsi surjeksi memetakan setiap elemen dari kodomain ke setidaknya satu elemen dari domain.

Contoh:

• f(x) = x, x ∈ R
• f(x) = |x|, x ∈ R

Bijeksi

Fungsi f: A → B dikatakan bijeksi jika fungsi tersebut injeksi dan surjeksi. Dengan kata lain, fungsi bijeksi memetakan elemen yang berbeda dari domain ke elemen yang berbeda dari kodomain, dan memetakan setiap elemen dari kodomain ke setidaknya satu elemen dari domain.

Contoh:

• f(x) = x + 1, x ∈ R
• f(x) = 2x, x ∈ R

Penerapan Fungsi

Fungsi memiliki penerapan luas dalam kehidupan sehari-hari dan berbagai bidang ilmu pengetahuan.

Dalam kehidupan sehari-hari, fungsi digunakan untuk:

• Membuat keputusan, seperti memilih rute terpendek saat bepergian.
• Menghitung biaya, seperti menghitung total belanjaan di toko.
• Menganalisis data, seperti menemukan tren dan pola dalam kumpulan data.

Dalam bidang ilmu pengetahuan, fungsi digunakan untuk:

• Matematika: Mempelajari hubungan antara variabel, seperti fungsi trigonometri.
• Fisika: Menjelaskan fenomena alam, seperti fungsi gerak.

li> Kimia: Memprediksi perilaku reaksi kimia, seperti fungsi laju reaksi.

• Ekonomi: Menganalisis tren ekonomi, seperti fungsi permintaan dan penawaran.

Kesimpulan Akhir

Fungsi f ditentukan oleh merupakan alat yang ampuh untuk memahami dan memprediksi hubungan dalam sistem dunia nyata.

Pemahaman tentang konsep ini sangat penting bagi siswa matematika, ilmuwan, dan siapa saja yang ingin menggunakan matematika untuk menyelesaikan masalah dan membuat keputusan yang tepat.

Pertanyaan Umum (FAQ)

Apa perbedaan antara fungsi injeksi dan fungsi surjeksi?

Fungsi injeksi adalah fungsi yang menetapkan setiap nilai input ke nilai output yang unik, sedangkan fungsi surjeksi adalah fungsi yang memetakan setiap nilai output ke setidaknya satu nilai input.

Bagaimana cara menentukan apakah suatu fungsi adalah bijeksi?

Suatu fungsi adalah bijeksi jika bersifat injeksi dan surjeksi.

Apa saja penerapan fungsi dalam kehidupan nyata?

Fungsi digunakan dalam berbagai bidang, seperti fisika (untuk menghitung jarak, kecepatan, dan percepatan), ekonomi (untuk memodelkan penawaran dan permintaan), dan ilmu komputer (untuk mengurutkan data dan mengompres file).