Dalam geometri, segitiga siku-siku memiliki sudut 90 derajat, menjadikannya alat penting dalam berbagai aplikasi. Memahami sifat, teorema, dan aplikasinya sangat penting untuk berbagai bidang seperti konstruksi, arsitektur, dan navigasi.

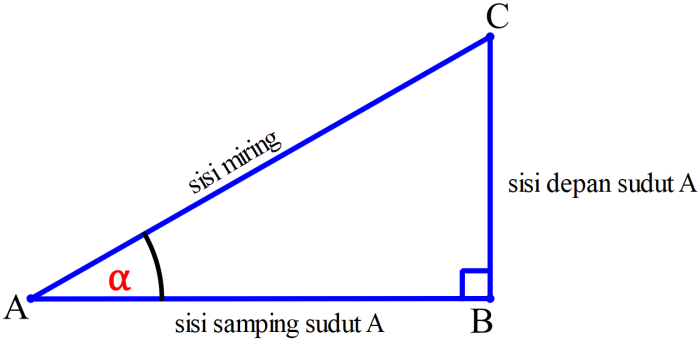
Segitiga siku-siku ABC terdiri dari sisi miring, sisi tegak, dan sisi alas. Sisi miring adalah sisi terpanjang yang berhadapan dengan sudut 90 derajat, sedangkan sisi tegak dan sisi alas adalah sisi lainnya.

Sifat Segitiga Siku-Siku ABC

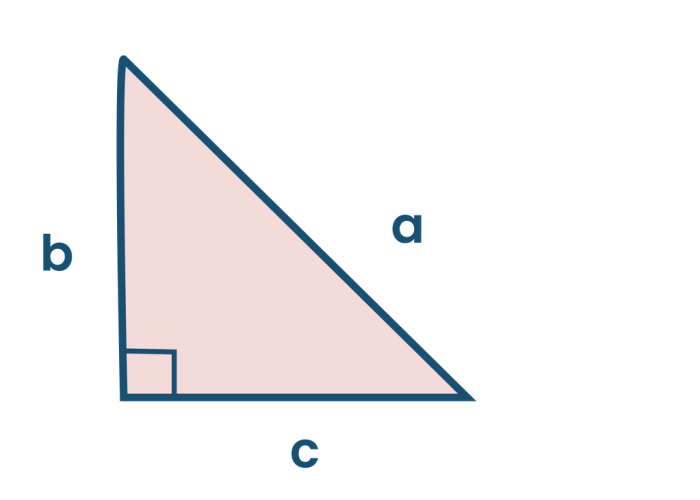
Segitiga siku-siku adalah segitiga yang memiliki satu sudut siku-siku (90 derajat). Segitiga siku-siku memiliki beberapa sifat khusus yang membedakannya dari jenis segitiga lainnya.

Sisi Miring, Sisi Tegak, dan Sisi Alas

Pada segitiga siku-siku ABC, sisi miring (c) adalah sisi yang berlawanan dengan sudut siku-siku. Sisi tegak (a) dan sisi alas (b) adalah sisi-sisi yang membentuk sudut siku-siku.

Teorema Pythagoras

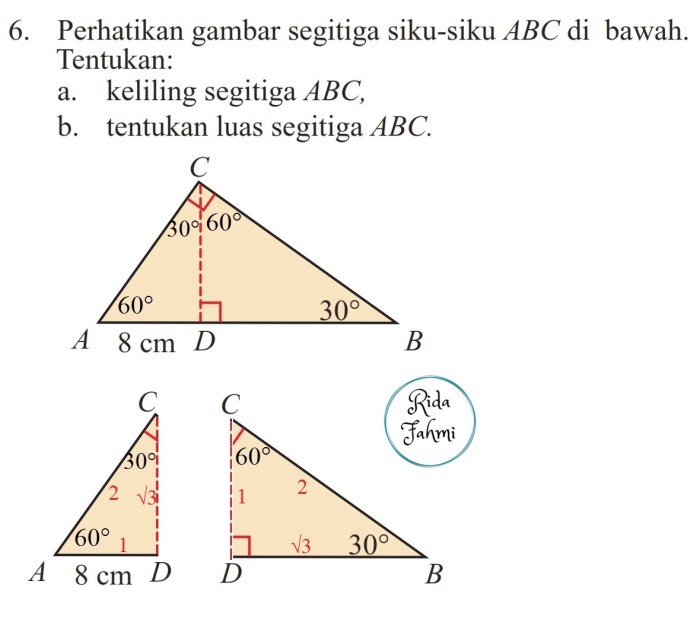
Teorema Pythagoras adalah teorema mendasar dalam geometri Euklides yang menyatakan hubungan antara panjang sisi-sisi segitiga siku-siku.

Teorema ini menyatakan bahwa dalam sebuah segitiga siku-siku, kuadrat panjang sisi miring (sisi terpanjang yang berlawanan dengan sudut siku-siku) sama dengan jumlah kuadrat panjang kedua sisi lainnya (sisi-sisi yang membentuk sudut siku-siku).

Contoh Penggunaan Teorema Pythagoras

Misalkan kita memiliki segitiga siku-siku ABC dengan sisi miring AB, sisi AC sepanjang 3 cm, dan sisi BC sepanjang 4 cm. Kita dapat menggunakan Teorema Pythagoras untuk mencari panjang sisi AB:

• AB² = AC² + BC²
• AB² = 3² + 4²
• AB² = 9 + 16
• AB² = 25
• AB = √25
• AB = 5 cm

Jadi, panjang sisi miring AB adalah 5 cm.

Trigonometri Segitiga Siku-Siku

Trigonometri adalah cabang matematika yang mempelajari hubungan antara sisi dan sudut segitiga. Dalam segitiga siku-siku, trigonometri digunakan untuk menghitung panjang sisi yang tidak diketahui dan besar sudut yang tidak diketahui.

Definisi Fungsi Trigonometri

Dalam segitiga siku-siku, ada tiga fungsi trigonometri yang umum digunakan, yaitu:

• Sinus (sin): Rasio sisi depan (berlawanan sudut) dengan sisi miring.
• Kosinus (cos): Rasio sisi samping (samping sudut) dengan sisi miring.
• Tangen (tan): Rasio sisi depan (berlawanan sudut) dengan sisi samping (samping sudut).

Hubungan Fungsi Trigonometri dengan Segitiga Siku-Siku

Hubungan fungsi trigonometri dengan segitiga siku-siku dapat dinyatakan dalam bentuk rumus:

sin θ = depan/miringcos θ = samping/miringtan θ = depan/samping

di mana θ adalah besar sudut yang berhadapan dengan sisi depan.

Menghitung Nilai Fungsi Trigonometri untuk Sudut Segitiga ABC

Untuk menghitung nilai fungsi trigonometri untuk sudut segitiga ABC, diperlukan informasi tentang panjang sisi segitiga. Misalnya, jika diketahui panjang sisi depan a, panjang sisi samping b, dan panjang sisi miring c, maka nilai fungsi trigonometri dapat dihitung sebagai berikut:

• sin θ = a/c
• cos θ = b/c
• tan θ = a/b

Aplikasi Segitiga Siku-Siku dalam Kehidupan Nyata

Segitiga siku-siku memiliki aplikasi luas dalam berbagai bidang kehidupan nyata, mulai dari konstruksi hingga navigasi. Sifat geometris uniknya membuatnya menjadi alat yang sangat berharga untuk menyelesaikan masalah dan membuat perhitungan.

Konstruksi

Segitiga siku-siku digunakan secara ekstensif dalam konstruksi untuk memastikan struktur yang kokoh dan stabil. Prinsip dasar segitiga siku-siku, seperti Teorema Pythagoras, memungkinkan arsitek dan insinyur untuk menghitung panjang sisi, sudut, dan beban yang bekerja pada struktur. Hal ini sangat penting untuk memastikan bangunan aman dan tahan lama.

Arsitektur

Dalam arsitektur, segitiga siku-siku memainkan peran penting dalam desain dan konstruksi bangunan. Mereka digunakan untuk menentukan sudut atap, ketinggian dinding, dan proporsi keseluruhan bangunan. Misalnya, arsitek menggunakan segitiga siku-siku untuk memastikan bahwa atap memiliki kemiringan yang tepat untuk drainase air yang efisien.

Navigasi

Segitiga siku-siku juga digunakan dalam navigasi, khususnya dalam navigasi laut dan udara. Kapten kapal dan pilot pesawat menggunakan prinsip segitiga siku-siku untuk menentukan posisi mereka, menghitung jarak yang ditempuh, dan merencanakan jalur perjalanan mereka. Misalnya, pilot menggunakan segitiga siku-siku untuk menghitung jarak antara dua titik di peta.

Ilustrasi Visual

Bagian ini memberikan ilustrasi visual untuk membantu memahami sifat-sifat dan hubungan antara sisi dan sudut segitiga siku-siku ABC.

Tabel Sifat-sifat Segitiga Siku-siku ABC

Tabel berikut merangkum sifat-sifat segitiga siku-siku ABC:

Sifat	Rumus
Sisi miring	$c^2\; =\; a^2\; +\; b^2$
Sudut siku-siku	90°
Jumlah sudut dalam	180°

Diagram Segitiga Siku-siku ABC

Diagram berikut menunjukkan hubungan antara sisi dan sudut segitiga siku-siku ABC:

• Sisi miring (c) adalah sisi terpanjang yang berlawanan dengan sudut siku-siku.
• Sisi siku-siku (a dan b) adalah sisi yang membentuk sudut siku-siku.
• Sudut siku-siku (∠C) adalah sudut yang berukuran 90°.
• Sudut lancip (∠A dan ∠B) adalah sudut yang lebih kecil dari 90°.

Ringkasan Terakhir

Memahami sifat dan aplikasi segitiga siku-siku sangat penting untuk berbagai bidang ilmu pengetahuan dan teknik. Dengan menggunakan Teorema Pythagoras dan fungsi trigonometri, segitiga siku-siku memungkinkan kita memecahkan masalah kompleks dan membuat perhitungan yang akurat dalam kehidupan nyata.

Pertanyaan Umum (FAQ)

Apa itu segitiga siku-siku?

Segitiga siku-siku adalah segitiga yang memiliki satu sudut 90 derajat.

Apa itu sisi miring?

Sisi miring adalah sisi terpanjang dari segitiga siku-siku yang berhadapan dengan sudut 90 derajat.

Bagaimana cara menggunakan Teorema Pythagoras?

Teorema Pythagoras menyatakan bahwa kuadrat sisi miring sama dengan jumlah kuadrat sisi tegak dan sisi alas.