Dalam ranah matematika, fungsi memainkan peran krusial dalam merepresentasikan hubungan antara variabel. Grafik fungsi, sebagai representasi visual dari hubungan ini, menjadi alat yang ampuh untuk memahami dan menganalisis fenomena di dunia nyata.

Dengan menguasai teknik menggambar grafik fungsi fx, kita membuka gerbang ke dunia pemecahan masalah yang kompleks dan prediksi tren yang akurat.

Pengertian Fungsi fx

Dalam matematika, fungsi adalah hubungan antara dua himpunan, yaitu domain dan range, di mana setiap elemen dalam domain dikaitkan dengan tepat satu elemen dalam range.

Fungsi umumnya dinyatakan dalam bentuk f(x), di mana f adalah nama fungsi dan x adalah variabel bebas (input). Hasil dari f(x) adalah variabel terikat (output).

Sifat-sifat Fungsi

Fungsi memiliki beberapa sifat penting, antara lain:

• Domain: Himpunan semua nilai input yang valid untuk fungsi tersebut.
• Range: Himpunan semua nilai output yang dihasilkan oleh fungsi tersebut.
• Injektif (Satu-ke-Satu): Jika setiap nilai input dikaitkan dengan tepat satu nilai output.
• Surjektif (Ke Atas): Jika setiap nilai output dikaitkan dengan setidaknya satu nilai input.
• Bijektif (Satu-ke-Satu dan Ke Atas): Jika fungsi tersebut injektif dan surjektif.

Menggambar Grafik Fungsi fx

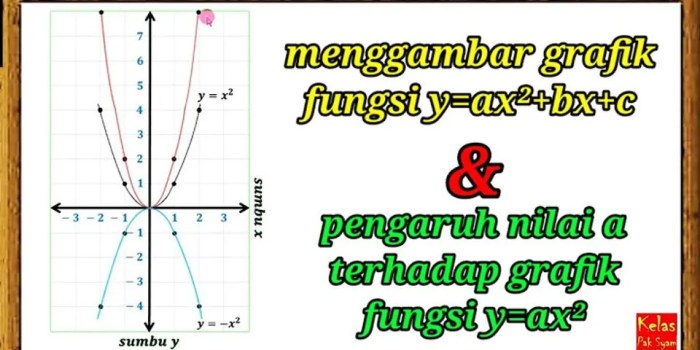
Menggambar grafik fungsi merupakan representasi visual hubungan antara variabel independen (x) dan variabel dependen (y). Koordinat kartesius, yang terdiri dari sumbu x dan y, digunakan untuk memplot titik-titik yang mewakili nilai fungsi untuk nilai x yang berbeda.

Langkah-Langkah Menggambar Grafik Fungsi

1. Tentukan Titik Potong: Temukan titik-titik di mana grafik memotong sumbu x dan y. Ini adalah titik-titik di mana y = 0 dan x = 0, masing-masing.
2. Temukan Titik Ekstrem: Cari nilai x yang menghasilkan nilai maksimum atau minimum fungsi. Ini dapat dilakukan dengan mencari turunan fungsi dan mencari titik-titik di mana turunannya sama dengan nol.
3. Buat Tabel Nilai: Pilih beberapa nilai x dan hitung nilai y yang sesuai. Ini akan memberi Anda titik-titik tambahan untuk diplot pada grafik.
4. Plot Titik-Titik: Plot titik-titik yang ditemukan pada langkah-langkah sebelumnya pada koordinat kartesius.
5. Hubungkan Titik-Titik: Hubungkan titik-titik dengan kurva halus untuk membentuk grafik fungsi.

Contoh Grafik Fungsi

Berikut adalah tabel beberapa fungsi umum dan grafiknya:

Fungsi	Grafik
y = x	Garis lurus melalui titik (0,0) dengan kemiringan 1
y = x2	Parabola yang terbuka ke atas dengan titik minimum di (0,0)
y = sin(x)	Gelombang sinusoid yang berosilasi antara 1 dan 1
y = e x	Kurva eksponensial yang meningkat dengan cepat

Transformasi Fungsi fx

Transformasi fungsi adalah operasi matematika yang mengubah grafik fungsi dengan cara tertentu.

Transformasi yang umum meliputi translasi, refleksi, dan dilatasi.

Translasi

Translasi menggeser grafik fungsi ke atas, bawah, kiri, atau kanan tanpa mengubah bentuknya. Jika fungsi f(x) ditranslasi sebesar a unit ke kanan dan b unit ke atas, fungsi yang dihasilkan adalah:

f'(x) = f(x

a) + b

Contoh: Grafik fungsi f(x) = x^2 ditranslasi 2 unit ke kanan dan 1 unit ke atas akan menghasilkan grafik f'(x) = (x – 2)^2 + 1.

Refleksi

Refleksi membalik grafik fungsi terhadap sumbu x atau y. Jika fungsi f(x) direfleksikan terhadap sumbu x, fungsi yang dihasilkan adalah:

f'(x) =

f(x)

Jika f(x) direfleksikan terhadap sumbu y, fungsi yang dihasilkan adalah:

f'(x) = f(-x)

Contoh: Grafik fungsi f(x) = x^2 direfleksikan terhadap sumbu x akan menghasilkan grafik f'(x) = -x^2.

Dilatasi

Dilatasi mengubah ukuran grafik fungsi dengan mengalikannya dengan faktor tertentu. Jika fungsi f(x) didilatasikan dengan faktor k, fungsi yang dihasilkan adalah:

f'(x) = kf(x)

Jika k > 1, grafik akan membesar. Jika k< 1, grafik akan mengecil.

Contoh: Grafik fungsi f(x) = x^2 didilatasikan dengan faktor 2 akan menghasilkan grafik f'(x) = 2x^2.

Aplikasi Grafik Fungsi fx

Grafik fungsi fx memiliki berbagai aplikasi penting dalam kehidupan nyata, terutama dalam bidang fisika dan ekonomi. Grafik ini memberikan representasi visual dari hubungan antara variabel dependen dan independen, sehingga memungkinkan kita untuk memahami dan memprediksi perilaku sistem.

Fisika

• Menghitung lintasan benda yang dilempar dengan kecepatan awal tertentu
• Membuat grafik hubungan antara waktu dan kecepatan suatu benda yang bergerak
• Menentukan percepatan benda yang jatuh bebas

Ekonomi

• Membuat grafik hubungan antara harga dan permintaan suatu barang
• Menganalisis tren pertumbuhan ekonomi dari waktu ke waktu
• Memprediksi fluktuasi pasar saham

Penutup

Menggambar grafik fungsi fx tidak hanya sekadar keterampilan teknis, tetapi juga seni yang menggabungkan pemahaman konseptual yang mendalam dan kreativitas visual. Dengan menguasai seni ini, kita memperoleh kemampuan untuk menjembatani kesenjangan antara matematika abstrak dan dunia nyata yang kompleks.

Jawaban yang Berguna

Mengapa menggambar grafik fungsi fx itu penting?

Grafik fungsi memberikan representasi visual dari hubungan antara variabel, memudahkan identifikasi tren, titik potong, dan sifat lainnya.

Apa langkah-langkah menggambar grafik fungsi fx?

Menentukan domain, menemukan titik potong sumbu, membuat tabel nilai, dan memplot titik-titik untuk menggambar kurva.

Bagaimana cara mentransformasikan grafik fungsi fx?

Translasi, refleksi, dan dilatasi dapat digunakan untuk memodifikasi grafik fungsi untuk merepresentasikan hubungan yang berbeda.