Garis 2x 3y 6 ditranslasikan dengan matriks – Dalam geometri, translasi garis merupakan operasi yang menggeser garis dalam arah dan jarak tertentu. Translasi garis 2x + 3y + 6 menggunakan matriks adalah metode yang efisien untuk melakukan operasi ini.

Matriks translasi adalah matriks persegi yang digunakan untuk menerjemahkan titik-titik pada garis. Dengan mengalikan koordinat titik dengan matriks translasi, titik tersebut akan bergeser sesuai dengan arah dan jarak yang ditentukan oleh matriks.

Pengertian Translasi Garis

Translasi garis adalah operasi geometri yang memindahkan setiap titik pada garis dengan jarak dan arah tertentu, tanpa mengubah kemiringan atau panjang garis. Translasi garis dapat didefinisikan sebagai berikut:

Rumus Translasi Garis

Misalkan garis ldiberikan oleh persamaan y = mx + c. Jika garis lditranslasikan sejauh (a, b), maka persamaan garis baru l’adalah:

y = mx + c + b

Perbedaan antara Translasi dan Rotasi

Translasi garis berbeda dengan rotasi garis. Rotasi garis melibatkan perputaran garis terhadap suatu titik, sedangkan translasi garis melibatkan pergeseran garis tanpa mengubah orientasinya.

Matriks Translasi

Matriks translasi adalah matriks yang digunakan untuk melakukan translasi atau perpindahan pada suatu garis atau bentuk geometri lainnya. Matriks translasi dapat digunakan untuk memindahkan garis dalam arah tertentu dan jarak tertentu.

Rumus matriks translasi untuk translasi dalam arah x dan y diberikan oleh:

Rumus Matriks Translasi

Matriks translasi 2×2:

$$T = \beginbmatrix 1 & 0 \\\ tx & 1 \endbmatrix$$

Matriks translasi 3×3:

$$T = \beginbmatrix 1 & 0 & 0 \\\ tx & 1 & 0 \\\ ty & 0 & 1 \endbmatrix$$

Garis 2x 3y 6 dapat ditranslasikan dengan menggunakan matriks. Proses ini melibatkan pergeseran garis dalam bidang koordinat tanpa mengubah kemiringannya. Untuk memahami translasi ini lebih lanjut, penting untuk buatlah pertanyaan dari hasil pengamatanmu . Dengan mengajukan pertanyaan tentang arah dan jarak translasi, kita dapat memperoleh pemahaman yang lebih baik tentang bagaimana matriks translasi memengaruhi posisi garis 2x 3y 6.

di mana:

• $$tx$$ adalah translasi dalam arah x
• $$ty$$ adalah translasi dalam arah y

Untuk menerapkan matriks translasi pada koordinat titik, matriks translasi dikalikan dengan koordinat titik tersebut. Hasil perkalian akan memberikan koordinat titik yang baru setelah ditranslasikan.

Translasi Garis Menggunakan Matriks

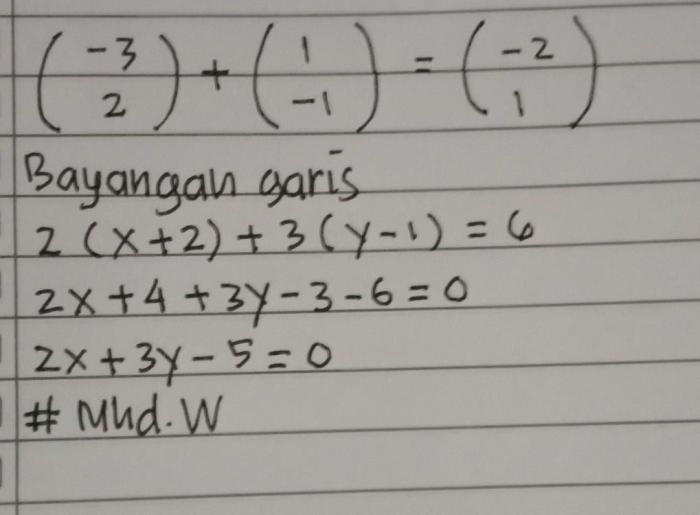
Translasi garis menggunakan matriks adalah metode untuk menggeser suatu garis dengan jumlah tertentu pada bidang koordinat. Metode ini melibatkan penerapan operasi matriks pada persamaan garis yang ada.

Langkah-langkah Translasi Garis Menggunakan Matriks

1. Tulis persamaan garis dalam bentuk matriks:

$$\beginbmatrixx\\\y\endbmatrix=\beginbmatrixa\\\b\endbmatrix+\beginbmatrixp\\\q\endbmatrixt$$

di mana:

• $\beginbmatrixx\\\y\endbmatrix$ adalah titik sembarang pada garis
• $\beginbmatrixa\\\b\endbmatrix$ adalah titik potong garis dengan sumbu $x$ dan $y$
• $\beginbmatrixp\\\q\endbmatrix$ adalah vektor translasi (jumlah pergeseran pada sumbu $x$ dan $y$)
• $t$ adalah parameter yang menentukan posisi titik pada garis
2. Buat matriks translasi:

$$\beginbmatrix1&0\\\0&1\endbmatrix+\beginbmatrixp\\\q\endbmatrix=\beginbmatrix1&0\\\0&1\endbmatrix\beginbmatrixp\\\q\endbmatrix$$

3. Kalikan matriks translasi dengan persamaan garis:

$$\beginbmatrix1&0\\\0&1\endbmatrix\beginbmatrixx\\\y\endbmatrix=\beginbmatrix1&0\\\0&1\endbmatrix\beginbmatrixa\\\b\endbmatrix+\beginbmatrix1&0\\\0&1\endbmatrix\beginbmatrixp\\\q\endbmatrixt$$

4. Sederhanakan persamaan yang dihasilkan:

$$\beginbmatrixx\\\y\endbmatrix=\beginbmatrixa+pt\\\b+qt\endbmatrix$$

5. Persamaan yang dihasilkan adalah persamaan garis yang telah ditranslasikan.

Contoh Translasi Garis Menggunakan Matriks

Misalkan kita memiliki garis $2x-3y+6=0$ yang ingin ditranslasikan sejauh $3$ satuan ke kanan dan $2$ satuan ke atas.

1. Tulis persamaan garis dalam bentuk matriks:

$$\beginbmatrixx\\\y\endbmatrix=\beginbmatrix3\\\2\endbmatrix+\beginbmatrix2\\\3\endbmatrixt$$

2. Buat matriks translasi:

$$\beginbmatrix1&0\\\0&1\endbmatrix+\beginbmatrix3\\\2\endbmatrix=\beginbmatrix1&0\\\0&1\endbmatrix\beginbmatrix3\\\2\endbmatrix$$

Garis 2x + 3y = 6 dapat ditranslasikan menggunakan matriks translasi. Proses ini melibatkan penerapan operasi matematika untuk menggeser garis ke lokasi baru pada bidang koordinat. Dalam konteks ini, konsep abstrak seperti “bisa dipegang gak bisa dilihat ada 6 huruf” (udara) dapat dianalogikan dengan translasi garis.

Udara, meski tidak terlihat, dapat dirasakan dan diukur, sama seperti garis yang dapat didefinisikan dan dimanipulasi secara matematis, meskipun keberadaannya tidak dapat dilihat secara langsung.

3. Kalikan matriks translasi dengan persamaan garis:

$$\beginbmatrix1&0\\\0&1\endbmatrix\beginbmatrixx\\\y\endbmatrix=\beginbmatrix1&0\\\0&1\endbmatrix\beginbmatrix3\\\2\endbmatrix+\beginbmatrix1&0\\\0&1\endbmatrix\beginbmatrix3\\\2\endbmatrixt$$

4. Sederhanakan persamaan yang dihasilkan:

$$\beginbmatrixx\\\y\endbmatrix=\beginbmatrix3+3t\\\2+2t\endbmatrix$$

5. Persamaan yang dihasilkan adalah persamaan garis yang telah ditranslasikan:

$$2x-3y+6=0\rightarrow2(x+3)-3(y+2)+6=0\rightarrow2x-3y+12=0$$

Ilustrasi Translasi Garis

Translasi garis adalah operasi geometris yang menggeser setiap titik pada garis dengan jarak dan arah tertentu. Translasi dapat digambarkan secara grafis menggunakan matriks translasi.

Matriks Translasi

Matriks translasi adalah matriks 2×2 yang digunakan untuk menggeser titik pada bidang. Bentuk umum matriks translasi adalah:

“`T = [a b] [c d]“`

Dimana:

• a adalah translasi sepanjang sumbu x
• b adalah translasi sepanjang sumbu y
• c adalah 0
• d adalah 1

Penerapan Matriks Translasi

Untuk menerjemahkan garis dengan persamaan y = mx + b menggunakan matriks translasi, titik-titik pada garis harus dikalikan dengan matriks translasi. Persamaan yang dihasilkan adalah:

“`[x’] [a b] [x][y’] = [c d] [y]“`

Garis 2x + 3y = 6 dapat ditranslasikan dengan matriks. Translasi ini melibatkan operasi penjumlahan vektor pada setiap titik pada garis. Dalam konteks bisnis, memahami perbedaan antara delivery note dan delivery order sangat penting untuk memastikan pengiriman barang yang efisien.

Delivery note berfungsi sebagai bukti pengiriman barang, sedangkan delivery order merupakan instruksi resmi untuk mengambil barang. Membedakan kedua dokumen ini sangat penting untuk menghindari kesalahan dalam proses pengiriman. Dengan memahami translasi garis 2x + 3y = 6 dan perbedaan antara delivery note dan delivery order, bisnis dapat memastikan pengiriman barang yang akurat dan tepat waktu.

Dimana:

• [x’, y’] adalah titik yang ditranslasikan
• [x, y] adalah titik asli
• [a b] adalah matriks translasi

Contoh Translasi Garis

Misalkan kita memiliki garis y = 2x + 1 dan kita ingin menerjemahkannya 3 unit ke kanan dan 2 unit ke atas. Matriks translasi untuk translasi ini adalah:

“`T = [1 3] [0 1]“`

Persamaan garis yang ditranslasikan adalah:

“`[x’] [1 3] [x][y’] = [0 1] [y]“““x’ = x + 3y’ = y + 2“`

Dengan demikian, garis y = 2x + 1 telah ditranslasikan menjadi garis y = 2x + 3.

Aplikasi Translasi Garis

Translasi garis merupakan operasi geometri yang memindahkan garis dengan jarak tertentu ke arah tertentu tanpa mengubah panjang atau orientasinya. Translasi garis memiliki aplikasi praktis dalam berbagai bidang, antara lain:

Desain Grafis, Garis 2x 3y 6 ditranslasikan dengan matriks

Dalam desain grafis, translasi garis digunakan untuk memindahkan dan memosisikan elemen desain, seperti gambar, teks, dan bentuk. Ini memungkinkan desainer untuk mengatur tata letak dan menciptakan komposisi yang harmonis.

Arsitektur

Dalam arsitektur, translasi garis digunakan untuk menggeser struktur bangunan, seperti dinding, jendela, dan pintu. Ini memungkinkan arsitek untuk menyesuaikan desain mereka dengan batasan situs dan persyaratan fungsional.

Animasi

Dalam animasi, translasi garis digunakan untuk menggerakkan objek dan menciptakan ilusi gerakan. Dengan memindahkan objek pada sumbu koordinat, animator dapat membuat efek dinamis dan realistis.

Ringkasan Penutup

Translasi garis menggunakan matriks memiliki banyak aplikasi praktis dalam berbagai bidang, seperti desain grafis, arsitektur, dan animasi. Metode ini memungkinkan manipulasi objek dan pembuatan efek visual yang kompleks dengan cara yang efisien dan akurat.

Kumpulan FAQ: Garis 2x 3y 6 Ditranslasikan Dengan Matriks

Apa perbedaan antara translasi dan rotasi?

Translasi menggeser objek dalam arah dan jarak tertentu, sedangkan rotasi memutar objek di sekitar titik tertentu.

Bagaimana cara menerapkan matriks translasi pada koordinat titik?

Koordinat titik dikalikan dengan matriks translasi untuk menghasilkan koordinat titik yang diterjemahkan.

Apa saja aplikasi praktis dari translasi garis?

Translasi garis digunakan dalam desain grafis, arsitektur, animasi, dan bidang lainnya untuk memanipulasi objek dan menciptakan efek visual.