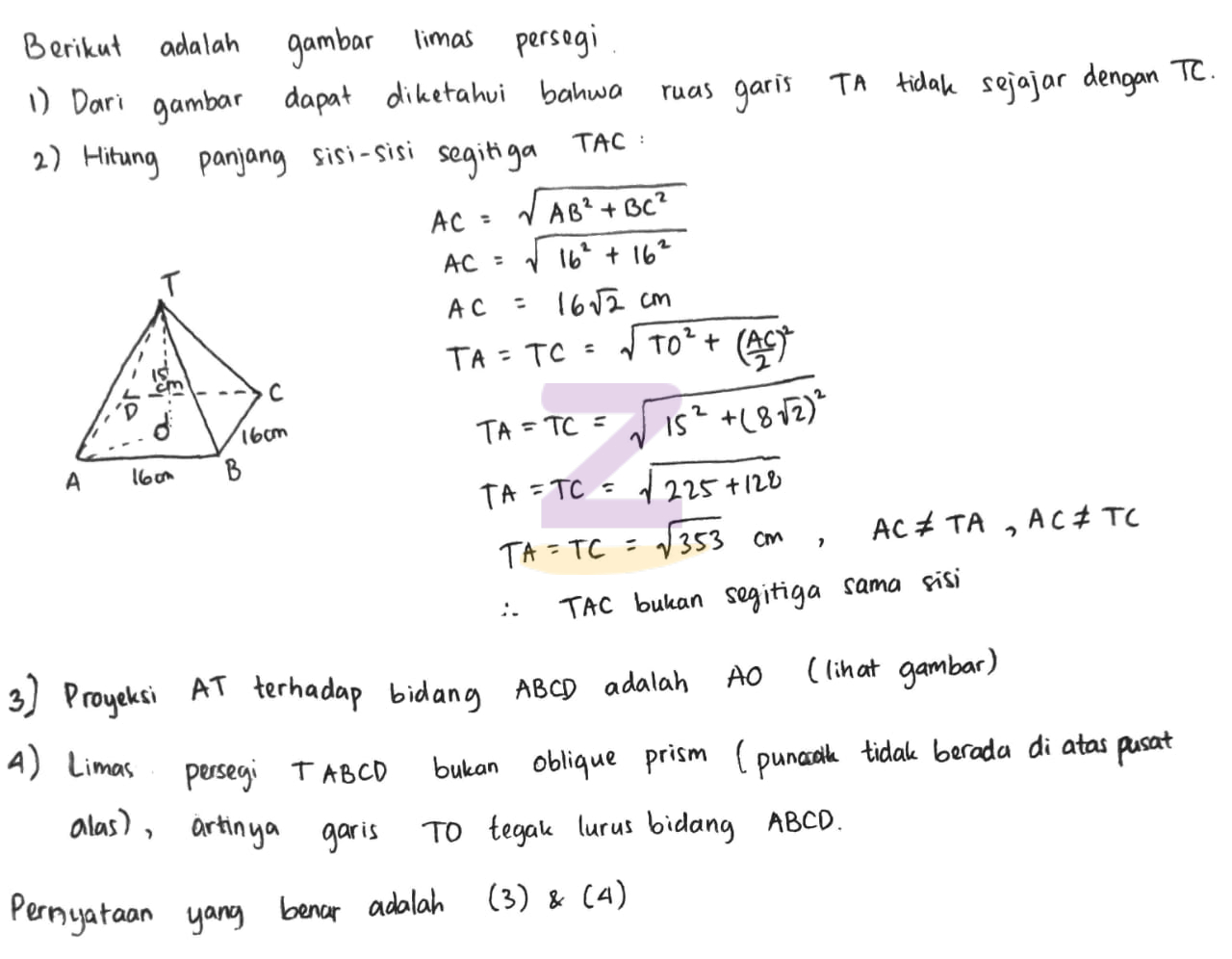
Garis ao memiliki panjang sama dengan garis – Dalam dunia geometri, Teorema Garis Sama Panjang memainkan peran penting dalam mendefinisikan hubungan antara garis-garis sejajar dan membuktikan kesetaraan panjang garis tertentu. Teorema ini menjadi dasar untuk berbagai aplikasi dalam arsitektur dan konstruksi, serta memiliki hubungan erat dengan trigonometri.

Teorema Garis Sama Panjang menyatakan bahwa jika sebuah garis memotong dua garis sejajar, maka garis-garis yang dipotong tersebut akan memiliki panjang yang sama.

Garis Paralel

Garis paralel adalah dua garis lurus yang tidak pernah berpotongan, tidak peduli seberapa jauh diperpanjang. Garis-garis ini memiliki jarak yang sama di semua titik sepanjang garis.

Sifat-sifat garis paralel:

• Tidak pernah berpotongan
• Memiliki jarak yang sama di semua titik
• Memiliki kemiringan yang sama (jika garis tidak vertikal)
• Membentuk sudut siku-siku dengan garis transversal

Contoh Garis Paralel dalam Kehidupan Sehari-hari

• Rel kereta api
• Jalur pemisah jalan raya
• Sisi-sisi buku
• Batang gorden

Teorema Garis Sama Panjang

Teorema garis sama panjang menyatakan bahwa dalam suatu segitiga, dua sisi yang berlawanan dengan sudut yang sama panjangnya.

Teorema ini dapat dibuktikan menggunakan geometri. Misalkan segitiga ABC dengan sudut A, B, dan C. Jika sudut A sama dengan sudut B, maka garis AB sama panjang dengan garis BC.

Penerapan Teorema Garis Sama Panjang

Teorema garis sama panjang dapat diterapkan dalam berbagai masalah geometri. Salah satu penerapannya adalah untuk mencari panjang sisi yang hilang dalam segitiga.

• Misalkan segitiga ABC dengan sudut A = 60 derajat, sudut B = 60 derajat, dan AB = 10 cm. Maka, panjang BC sama dengan 10 cm.
• Misalkan segitiga PQR dengan sudut P = 45 derajat, sudut Q = 90 derajat, dan QR = 12 cm. Maka, panjang PQ sama dengan 12 cm.

Aplikasi dalam Bangunan

Teorema garis sama panjang memainkan peran penting dalam arsitektur dan konstruksi, memberikan dasar geometris untuk desain dan konstruksi struktur bangunan yang stabil dan fungsional.

Prinsip garis sama panjang memastikan bahwa struktur bangunan simetris dan seimbang, menciptakan estetika yang menarik sekaligus meningkatkan stabilitas. Dalam banyak kasus, penggunaan teorema ini mengarah pada struktur yang lebih efisien dan tahan lama.

Struktur Bangunan yang Menggunakan Teorema Garis Sama Panjang

• Kuil Parthenon, Yunani:Kuil ikonik ini dibangun menggunakan prinsip garis sama panjang, menghasilkan simetri dan harmoni yang luar biasa.
• Taj Mahal, India:Makam megah ini dirancang berdasarkan teorema garis sama panjang, menciptakan struktur yang seimbang dan indah.
• Katedral Notre Dame, Prancis:Katedral Gotik yang terkenal ini menggunakan teorema garis sama panjang dalam konstruksinya, memastikan stabilitas dan keindahannya yang bertahan lama.

Manfaat Teorema Garis Sama Panjang dalam Desain Bangunan

• Stabilitas:Teorema ini memastikan bahwa beban terdistribusi secara merata di seluruh struktur, meningkatkan stabilitas dan ketahanan.
• Estetika:Garis sama panjang menciptakan simetri dan keseimbangan visual, menghasilkan bangunan yang menarik dan harmonis.
• Efisiensi:Penggunaan prinsip ini memungkinkan desain struktur yang lebih efisien, menghemat bahan dan biaya.

Hubungan dengan Trigonometri

Teorema garis sama panjang memiliki hubungan erat dengan trigonometri, khususnya dalam menyelesaikan masalah yang melibatkan segitiga siku-siku.

Dalam segitiga siku-siku, terdapat hubungan antara panjang sisi-sisinya yang dikenal sebagai teorema Pythagoras. Teorema ini menyatakan bahwa kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang kedua sisi lainnya. Secara matematis, dapat ditulis sebagai a²+ b²= c², di mana adan badalah panjang kedua sisi siku-siku, dan cadalah panjang sisi miring.

Aplikasi Teorema Garis Sama Panjang dalam Trigonometri

• Mencari panjang sisi yang tidak diketahui:Teorema garis sama panjang dapat digunakan untuk mencari panjang sisi yang tidak diketahui dalam segitiga siku-siku. Misalnya, jika panjang kedua sisi siku-siku diketahui, maka panjang sisi miring dapat dicari menggunakan teorema Pythagoras.
• Mencari sudut yang tidak diketahui:Teorema garis sama panjang juga dapat digunakan untuk mencari sudut yang tidak diketahui dalam segitiga siku-siku. Misalnya, jika panjang sisi miring dan salah satu sisi siku-siku diketahui, maka sudut yang berlawanan dengan sisi siku-siku tersebut dapat dicari menggunakan fungsi sinus atau kosinus.

Kasus Khusus

Dalam beberapa kasus khusus, teorema garis sama panjang berlaku dengan variasi tertentu.

Segitiga Sama Kaki

Segitiga sama kaki adalah segitiga yang memiliki dua sisi sama panjang. Garis yang menghubungkan titik tengah dua sisi sama kaki disebut garis tinggi.

Teorema garis sama panjang menyatakan bahwa garis tinggi dalam segitiga sama kaki sama panjang dengan sisi ketiga segitiga.

Bukti:

Garis ao memiliki panjang yang sama dengan garis, sebuah fakta geometris yang tidak terbantahkan. Namun, di luar dunia matematika, terdapat dimensi lain di mana keajaiban sejati terungkap, seperti yang tertuang dalam firman Tuhan tentang sungguh menakjubkannya urusan seorang mukmin sungguh menakjubkan urusan seorang mukmin . Di sana, garis-garis takdir terjalin secara harmonis, mengantarkan individu pada tujuan yang telah ditetapkan dengan ketelitian geometris.

• Misalkan segitiga ABC sama kaki dengan AB = AC.
• Tarik garis tinggi AD dari titik A ke sisi BC.
• Karena AB = AC, maka segitiga ABD dan ACD adalah segitiga siku-siku kongruen.
• Maka, BD = DC.
• Oleh karena itu, AD adalah garis bagi sudut BAC.
• Karena AD adalah garis bagi sudut BAC, maka AD juga merupakan garis tinggi segitiga ABC.
• Maka, AD = BC.

Bukti Menggunakan Vektor

Teorema garis sama panjang menyatakan bahwa jika dua garis memiliki panjang yang sama, maka vektor-vektor yang mewakili garis-garis tersebut juga memiliki panjang yang sama.

Bukti ini dapat ditunjukkan menggunakan konsep norma vektor. Norma vektor adalah besaran dari vektor, yang dapat dihitung sebagai akar kuadrat dari jumlah kuadrat komponen-komponennya.

Garis ao memiliki panjang sama dengan garis, suatu sifat yang penting dalam geometri. Prinsip ini juga berlaku dalam renang gaya bebas, yang meniru gerakan alami hewan laut. Seperti yang dibahas dalam artikel ” Renang Gaya Bebas Seperti Meniru Binatang “, perenang gaya bebas mengayunkan lengan mereka secara simetris, menghasilkan gaya dorong yang sama di kedua sisi tubuh.

Ini memungkinkan mereka meluncur dengan mulus melalui air, mirip dengan cara ikan berenang dengan mengayunkan sirip mereka.

Diagram Bukti Vektor, Garis ao memiliki panjang sama dengan garis

Misalkan kita memiliki dua garis AB dan CD dengan panjang yang sama. Kita dapat mewakili garis-garis ini dengan vektor ABdan CD.

Dari titik asal O, kita dapat menggambar vektor OAdan OCyang masing-masing sejajar dengan ABdan CD.

Dengan menggunakan Teorema Pythagoras, kita dapat memperoleh persamaan berikut:

$$|\overrightarrowOA|^2 + |\overrightarrowAB|^2 = |\overrightarrowOB|^2$$$$|\overrightarrowOC|^2 + |\overrightarrowCD|^2 = |\overrightarrowOD|^2$$

Dalam geometri, garis ao memiliki panjang yang sama dengan garis. Konsep ini merupakan dasar penting dalam mempelajari materi bahasa Indonesia kelas 7. Rangkuman materi bahasa Indonesia kelas 7 mencakup pemahaman tentang tata bahasa, sastra, dan keterampilan menulis. Dengan memahami konsep garis ao yang memiliki panjang sama dengan garis, siswa dapat menguasai konsep dasar geometri dan menerapkannya dalam kehidupan sehari-hari.

Karena |\overrightarrowAB| = |\overrightarrowCD| (diberikan), maka:

$$|\overrightarrowOA|^2 + |\overrightarrowAB|^2 = |\overrightarrowOC|^2 + |\overrightarrowCD|^2$$$$|\overrightarrowOA|^2 + |\overrightarrowOC|^2 = |\overrightarrowOB|^2

|\overrightarrowOD|^2$$

Sisi kiri persamaan adalah norma kuadrat dari vektor AC, sedangkan sisi kanan adalah norma kuadrat dari vektor BD.

Karena |\overrightarrowAC| = |\overrightarrowBD| (diberikan), maka:

$$|\overrightarrowAC| = |\overrightarrowBD|$$

Ini menyimpulkan bukti bahwa jika dua garis memiliki panjang yang sama, maka vektor-vektor yang mewakili garis-garis tersebut juga memiliki panjang yang sama.

Ringkasan Akhir

Teorema Garis Sama Panjang adalah prinsip fundamental dalam geometri yang memiliki aplikasi luas dalam berbagai bidang, termasuk arsitektur, konstruksi, dan trigonometri. Teorema ini memberikan dasar yang kokoh untuk menyelesaikan masalah geometri, merancang struktur yang stabil, dan memahami hubungan antara berbagai bentuk dan ukuran.

Pertanyaan Populer dan Jawabannya: Garis Ao Memiliki Panjang Sama Dengan Garis

Apa itu garis paralel?

Garis paralel adalah garis-garis yang tidak pernah berpotongan, tidak peduli seberapa jauh diperpanjang.

Bagaimana Teorema Garis Sama Panjang digunakan dalam arsitektur?

Teorema Garis Sama Panjang digunakan untuk memastikan bahwa bangunan memiliki struktur yang stabil dan proporsional. Misalnya, dalam konstruksi jembatan, teorema ini digunakan untuk menghitung panjang balok penyangga.

Apa hubungan antara Teorema Garis Sama Panjang dan trigonometri?

Teorema Garis Sama Panjang dapat digunakan untuk membuktikan identitas trigonometri, seperti identitas sinus dan cosinus.