Dalam dunia matematika, grafik fungsi trigonometri memainkan peran penting dalam memodelkan fenomena periodik dan memahami konsep matematika yang kompleks. Di antara fungsi trigonometri tersebut, grafik fungsi y = sin x menonjol karena bentuknya yang unik dan aplikasinya yang luas.

Grafik fungsi y = sin x adalah representasi visual dari hubungan antara sudut dan nilai sinusnya. Memahami karakteristik dan sifat grafik ini sangat penting untuk menguasai trigonometri dan penerapannya dalam berbagai bidang.

Definisi dan Rumus Grafik Fungsi Trigonometri y = sin x

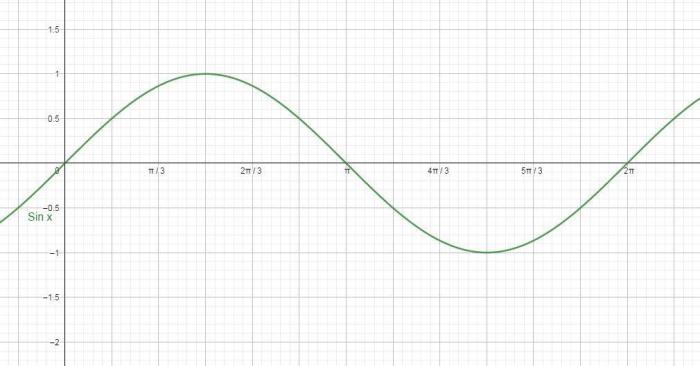
Fungsi trigonometri sin x adalah salah satu fungsi trigonometri dasar yang merepresentasikan rasio sisi depan segitiga siku-siku terhadap sisi miring, dengan sudut yang berhadapan dengan sisi depan adalah x. Grafik fungsi sin x berbentuk gelombang sinusoidal yang berosilasi antara -1 dan 1.

Rumus Umum Grafik Fungsi y = sin x

Rumus umum grafik fungsi y = sin x adalah:

y = A sin(Bx + C) + D

• A adalah amplitudo, yang menentukan tinggi gelombang.
• B adalah frekuensi sudut, yang menentukan jumlah osilasi per satuan sudut.
• C adalah pergeseran fase, yang menentukan pergeseran horizontal grafik.
• D adalah pergeseran vertikal, yang menentukan pergeseran vertikal grafik.

Sifat-Sifat Dasar Grafik Fungsi sin x

Sifat-sifat dasar grafik fungsi sin x meliputi:

• Periode: 2π
• Amplitudo: 1
• Nilai minimum:
  -1
• Nilai maksimum: 1
• Grafik berosilasi antara
  -1 dan 1.
• Grafik memiliki titik nol pada kelipatan π.
• Grafik memiliki titik maksimum pada kelipatan π/2.
• Grafik memiliki titik minimum pada kelipatan 3π/2.

Karakteristik Grafik Fungsi y = sin x

Bentuk Umum Grafik Fungsi sin x

Grafik fungsi y = sin x memiliki bentuk seperti gelombang sinus. Gelombang sinus ditandai dengan pola berulang dari puncak dan lembah yang halus.

Titik-Titik Penting pada Grafik

• Titik Puncak: (2nπ, 1), di mana n adalah bilangan bulat.
• Titik Lembah: (2nπ + π,
  -1), di mana n adalah bilangan bulat.
• Titik Potong Sumbu-x: (nπ, 0), di mana n adalah bilangan bulat.

Transformasi Grafik sin x

• Pergeseran Vertikal: y = sin x + k menggeser grafik ke atas sebesar k unit jika k > 0, dan ke bawah sebesar k unit jika k < 0.
• Pergeseran Horizontal: y = sin (x
  – h) menggeser grafik ke kanan sebesar h unit jika h > 0, dan ke kiri sebesar h unit jika h < 0.
• Peregangan Vertikal: y = a sin x meregangkan grafik secara vertikal dengan faktor |a|.
• Peregangan Horizontal: y = sin bx memampatkan grafik secara horizontal dengan faktor 1/b.
• Refleksi: y =
  -sin x merefleksikan grafik terhadap sumbu x.

Aplikasi Grafik Fungsi y = sin x

Grafik fungsi y = sin x memiliki berbagai aplikasi penting dalam kehidupan nyata, teknik, fisika, dan matematika. Grafik ini digunakan untuk memodelkan fenomena periodik, seperti gelombang suara, getaran, dan osilasi.

Contoh Aplikasi dalam Kehidupan Nyata

Grafik sin x digunakan untuk menganalisis dan memahami berbagai fenomena gelombang, seperti:

Gelombang suara

Grafik sin x digunakan untuk memodelkan gelombang suara yang merambat melalui udara atau medium lain.

Getaran

Grafik sin x digunakan untuk menganalisis getaran benda, seperti pegas atau pendulum.

Osilasi

Grafik sin x digunakan untuk memodelkan osilasi sistem fisik, seperti ayunan atau pegas.

Peran dalam Teknik, Fisika, dan Matematika

Dalam teknik, grafik sin x digunakan dalam desain dan analisis sistem kelistrikan, mekanik, dan akustik. Dalam fisika, grafik sin x digunakan untuk memahami fenomena gelombang dan getaran. Dalam matematika, grafik sin x digunakan sebagai dasar untuk fungsi trigonometri lainnya dan merupakan alat penting untuk analisis fungsi periodik.

Pemodelan Fenomena Periodik

Grafik sin x sangat efektif untuk memodelkan fenomena periodik karena sifat periodiknya. Grafik ini menunjukkan pola berulang yang dapat digunakan untuk memprediksi perilaku sistem periodik dari waktu ke waktu.

Pembuatan Grafik Fungsi y = sin x

Fungsi trigonometri y = sin x merupakan fungsi periodik yang menggambarkan gerakan harmonik sederhana. Untuk membuat grafik fungsi ini, perlu mengikuti langkah-langkah berikut:

Susun Tabel Nilai

Susun tabel nilai untuk fungsi y = sin x pada interval tertentu, misalnya [-π, π]. Pilih titik-titik dengan jarak yang sama untuk memastikan grafik yang akurat.

Plot Titik dan Hubungkan Garis

Plot titik-titik dari tabel nilai pada bidang koordinat. Titik-titik tersebut akan membentuk kurva sinus. Hubungkan titik-titik tersebut dengan garis halus untuk membuat grafik fungsi y = sin x.

Tips dan Trik

• Gunakan skala yang sesuai pada sumbu x dan y untuk memastikan grafik yang proporsional.
• Perhatikan titik-titik penting, seperti titik puncak, titik nol, dan titik balik.
• Manfaatkan simetri fungsi sin x terhadap sumbu x dan sumbu y.

Perbandingan dengan Fungsi Trigonometri Lainnya

Fungsi trigonometri sin x dapat dibandingkan dengan fungsi trigonometri lainnya seperti cos x dan tan x. Masing-masing fungsi ini memiliki karakteristik dan grafik yang unik.

Cosinus (cos x)

• Cosinus adalah fungsi genap, artinya simetris terhadap sumbu y.
• Grafik cos x adalah kurva berbentuk gelombang yang berosilasi antara 1 dan
  -1.
• Cos x bergeser 90 derajat ke kiri dibandingkan dengan sin x.

Tangen (tan x)

• Tangen adalah fungsi ganjil, artinya simetris terhadap titik asal.
• Grafik tan x adalah kurva dengan asimtot vertikal pada x = π/2 dan x = 3π/2.
• Tan x tidak memiliki periode dan bernilai tak hingga saat x mendekati asimtotnya.

Turunan Fungsi Trigonometri

Grafik fungsi trigonometri lainnya dapat diturunkan dari grafik sin x melalui proses diferensiasi.

• Turunan sin x adalah cos x.
• Turunan cos x adalah
  -sin x.
• Turunan tan x adalah sec² x.

Penutupan

Grafik fungsi y = sin x tidak hanya sekadar representasi matematika, tetapi juga alat yang ampuh untuk memecahkan masalah di dunia nyata. Pemahaman yang mendalam tentang grafik ini membuka pintu untuk aplikasi yang tak terhitung jumlahnya dalam teknik, fisika, dan bidang lainnya.

Dengan menguasai grafik fungsi y = sin x, kita dapat lebih menghargai keindahan dan kegunaan matematika dalam kehidupan kita sehari-hari.

Pertanyaan Umum (FAQ)

Apa periode grafik fungsi y = sin x?

Periode grafik fungsi y = sin x adalah 2π, yang berarti grafiknya berulang setiap 2π unit pada sumbu x.

Apa amplitudo grafik fungsi y = sin x?

Amplitudo grafik fungsi y = sin x adalah 1, yang berarti nilai maksimum dan minimumnya masing-masing adalah 1 dan -1.

Apa titik potong sumbu x pada grafik fungsi y = sin x?

Grafik fungsi y = sin x memotong sumbu x pada titik (0, 0), (π, 0), (2π, 0), dan seterusnya.