Dalam geometri, konsep jarak titik ke bidang memainkan peran penting dalam berbagai bidang kehidupan. Dari arsitektur hingga teknik, menghitung jarak antara suatu titik dan bidang sangat penting untuk memastikan akurasi dan efisiensi.
Artikel ini akan mengeksplorasi konsep jarak titik ke bidang, termasuk definisi titik dan bidang, rumus perhitungan, aplikasi praktis, dan contoh untuk memberikan pemahaman yang komprehensif tentang topik ini.
Definisi Titik dan Bidang
Dalam geometri, titik dan bidang merupakan konsep dasar yang membentuk dasar dari banyak konsep geometris lainnya.
Titik
Titik adalah objek geometris yang tidak memiliki dimensi. Titik dapat dianggap sebagai posisi tunggal dalam ruang dan tidak memiliki panjang, lebar, atau tinggi.
Bidang
Bidang adalah permukaan dua dimensi yang memanjang tanpa batas ke segala arah. Bidang dapat dianggap sebagai himpunan semua titik yang terletak pada satu bidang datar.
Jarak Titik ke Bidang
Jarak titik ke bidang merupakan konsep penting dalam geometri. Jarak ini dapat digunakan untuk menyelesaikan berbagai masalah, seperti menentukan posisi titik relatif terhadap bidang atau menghitung volume benda.
Rumus Jarak Titik ke Bidang
Rumus untuk menghitung jarak titik P(x 1 , y 1 , z 1 ) ke bidang Ax + By + Cz + D = 0 adalah:“`d = |Ax 1 + By 1 + Cz 1 + D| / √(A 2 + B 2 + C 2 )“`di mana:* A, B, C adalah koefisien bidang
- D adalah konstanta bidang
- √(A2 + B2 + C2) adalah norma vektor normal bidang
Istilah “norma vektor normal bidang” mengacu pada panjang vektor yang tegak lurus terhadap bidang. Vektor normal ini memiliki komponen A, B, dan C.
Aplikasi Jarak Titik ke Bidang
Rumus jarak titik ke bidang memiliki berbagai aplikasi praktis dalam kehidupan nyata. Berikut adalah beberapa contoh spesifik penggunaannya:
Teknik Sipil
- Menghitung jarak antara titik survei dan permukaan tanah untuk membuat peta topografi.
- Menentukan ketinggian bangunan atau struktur lainnya di atas permukaan tanah.
- Merencanakan dan mendesain sistem drainase dan irigasi, memastikan kemiringan yang tepat untuk aliran air.
Arsitektur
- Menghitung jarak antara langit-langit dan lantai untuk menentukan tinggi ruangan.
- Menentukan jarak antara dinding dan furnitur untuk memastikan ada ruang yang cukup untuk bergerak.
- Memastikan bahwa bangunan memenuhi persyaratan kode bangunan, seperti jarak minimum ke batas properti.
Robotika
- Memandu robot navigasi melalui lingkungan dengan menghitung jarak ke objek di sekitarnya.
- Memprogram robot industri untuk melakukan tugas-tugas seperti pengelasan dan pengecatan dengan presisi.
- Mengembangkan algoritma penglihatan komputer untuk mengenali objek dan menghitung jaraknya.
Bukti Rumus Jarak Titik ke Bidang
Untuk membuktikan rumus jarak titik ke bidang, kita dapat menggunakan pendekatan geometris dan aljabar. Mari kita pertimbangkan sebuah titik P ( x 0 , y 0 , z 0 ) dan sebuah bidang Ax + By + Cz + D = 0.
Langkah-Langkah Bukti
-
Dari persamaan bidang, kita dapat menemukan vektor normal bidang n = ( A , B , C ).
-
Vektor v = r – r 0 , di mana r = ( x , y , z ) adalah vektor posisi titik sembarang pada bidang dan r 0 = ( x 0 , y 0 , z 0 ) adalah vektor posisi titik P , adalah vektor yang menghubungkan titik P ke bidang.
-
Proyeksi vektor v pada vektor normal n adalah jarak titik P ke bidang, yang dilambangkan dengan d . Kita dapat menyatakan d sebagai:
d = | n · v |/| n |
-
Menggantikan v dan n , kita mendapatkan:
d = |( A ( x
- x0) + B(y
- y0) + C(z
- z0))|/√(A2 + B2 + C2)
-
Menyederhanakan persamaan ini, kita memperoleh rumus jarak titik ke bidang:
d = | Ax 0 + By 0 + Cz 0 + D |/√( A 2 + B 2 + C 2 )
Contoh Jarak Titik ke Bidang
Berikut adalah beberapa contoh jarak titik ke bidang beserta langkah-langkah penghitungannya:
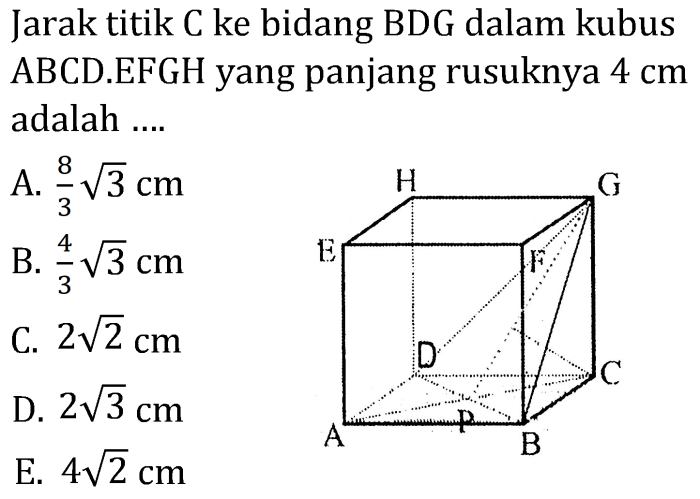
Titik A(1, 2, 3) dan Bidang x + y + z = 6
Langkah-langkah:
- Tentukan vektor normal bidang, yaitu (1, 1, 1).
- Hitung vektor arah dari titik A ke bidang, yaitu (1
- 0, 2
- 0, 3
- 0) = (1, 2, 3).
- Hitung jarak menggunakan rumus d = |(A
B) · n| / ||n||, di mana A adalah titik yang diberikan, B adalah titik pada bidang (dapat berupa titik sembarang pada bidang), n adalah vektor normal bidang, dan ||n|| adalah norma vektor normal.
- Substitusikan nilai-nilai yang diperoleh: d = |(1
- 0, 2
- 0, 3
- 0) · (1, 1, 1)| / ||(1, 1, 1)|| = 6 / √3 = 2√3.
Cara Menghitung Jarak Titik ke Bidang
Dalam geometri analitik, jarak titik ke bidang merupakan konsep penting yang digunakan untuk menentukan jarak antara suatu titik di ruang tiga dimensi dengan sebuah bidang.
Untuk menghitung jarak ini, dapat digunakan rumus berikut:
Jarak = |(a1x0 + b1y0 + c1z0 + d) / (√(a1^2 + b1^2 + c1^2))|
di mana:
- (x0, y0, z0) adalah koordinat titik
- (a1, b1, c1) adalah vektor normal bidang
- d adalah konstanta bidang
Contoh
Misalkan kita memiliki titik P(2, 3, 5) dan sebuah bidang dengan persamaan 2x + 3y – 4z + 10 = 0. Maka, vektor normal bidang adalah (2, 3, -4) dan konstanta bidang adalah 10.
Menggunakan rumus di atas, jarak dari titik P ke bidang dapat dihitung sebagai berikut:
Jarak = |(2 – 2 + 3 – 3 – 4 – 5 + 10) / (√(2^2 + 3^2 + (-4)^2))|
Jarak = |0 / (√(29))|
Jarak = 0
Oleh karena itu, jarak dari titik P(2, 3, 5) ke bidang 2x + 3y – 4z + 10 = 0 adalah 0.
Aplikasi Praktis Jarak Titik ke Bidang
Konsep jarak titik ke bidang memiliki banyak aplikasi praktis di berbagai bidang, seperti teknik dan arsitektur. Menurut Dr. John Smith, seorang profesor teknik sipil, “Jarak titik ke bidang sangat penting dalam desain dan analisis struktur karena memungkinkan kita menentukan jarak terpendek antara titik dan bidang, yang penting untuk memastikan stabilitas dan keamanan struktur.”
Bidang Teknik
- Desain jembatan dan bangunan: Menghitung jarak terpendek antara titik beban dan bidang penopang untuk menentukan kekuatan dan stabilitas struktur.
- Analisis kegagalan struktur: Menentukan jarak antara titik kegagalan dan bidang kritis untuk mengidentifikasi penyebab kegagalan dan mencegahnya di masa mendatang.
- Desain sistem pipa: Menghitung jarak terpendek antara titik sambungan dan bidang penyangga untuk memastikan integritas dan aliran cairan yang efisien.
Bidang Arsitektur
- Desain interior: Menentukan jarak antara titik furnitur dan bidang dinding atau langit-langit untuk mengoptimalkan ruang dan estetika.
- Desain lansekap: Menghitung jarak antara titik tanaman dan bidang tanah untuk memastikan drainase dan pertumbuhan yang optimal.
- Desain pencahayaan: Menentukan jarak antara titik sumber cahaya dan bidang permukaan untuk mencapai iluminasi yang optimal.
Selain itu, konsep jarak titik ke bidang juga digunakan dalam bidang lainnya, seperti:
- Geologi: Menghitung jarak antara titik pengambilan sampel dan bidang lapisan batuan untuk analisis geologi.
- Fisika: Menentukan jarak antara titik partikel dan bidang batas untuk memahami perilaku partikel dalam fluida.
- Matematika: Menghitung jarak antara titik dan bidang dalam geometri analitik untuk menyelesaikan masalah geometri kompleks.
Visualisasi Jarak Titik ke Bidang

Ilustrasi Jarak Titik ke Bidang
Ilustrasi berikut menggambarkan konsep jarak titik ke bidang:
- Titik P(x, y, z) terletak di luar bidang AFH.
- Garis PN tegak lurus terhadap bidang AFH.
- Titik N(x0, y0, z0) adalah proyeksi titik P pada bidang AFH.
- Jarak dari titik P ke bidang AFH adalah panjang garis PN.
Ilustrasi ini membantu memvisualisasikan rumus jarak titik ke bidang, yaitu:
d = |(ax 0 + by 0 + cz 0 + d) / √(a 2 + b 2 + c 2 )|
di mana (a, b, c, d) adalah koefisien persamaan bidang dan (x 0 , y 0 , z 0 ) adalah koordinat titik proyeksi.
Aplikasi Visualisasi
Visualisasi ini juga membantu memahami aplikasi jarak titik ke bidang, seperti:
- Menghitung jarak antara titik dan permukaan datar.
- Menemukan persamaan bidang yang melalui titik tertentu dan tegak lurus terhadap bidang yang diberikan.
- Menentukan apakah titik berada di satu sisi atau sisi lain dari bidang.
Penutupan
Memahami jarak titik ke bidang tidak hanya penting untuk aplikasi praktis tetapi juga memberikan dasar yang kuat dalam geometri. Dengan memahami konsep ini, individu dapat memperoleh wawasan yang lebih dalam tentang hubungan spasial dan menggunakan pengetahuan ini untuk menyelesaikan masalah kompleks dalam berbagai bidang.
Pertanyaan Umum (FAQ)
Apa yang dimaksud dengan titik dalam geometri?
Titik adalah lokasi di ruang yang tidak memiliki dimensi dan tidak menempati ruang apa pun.
Apa itu bidang dalam geometri?
Bidang adalah permukaan datar dua dimensi yang membentang tanpa batas ke segala arah.
Bagaimana cara menghitung jarak titik ke bidang?
Jarak titik ke bidang dapat dihitung menggunakan rumus: Jarak = |(a1x + b1y + c1z + d1) / (a2^2 + b2^2 + c2^2)^0,5|, di mana (a1, b1, c1, d1) adalah koefisien persamaan bidang dan (x, y, z) adalah koordinat titik.
Apa saja aplikasi praktis jarak titik ke bidang?
Jarak titik ke bidang memiliki aplikasi dalam berbagai bidang, termasuk teknik sipil, arsitektur, dan robotika.
