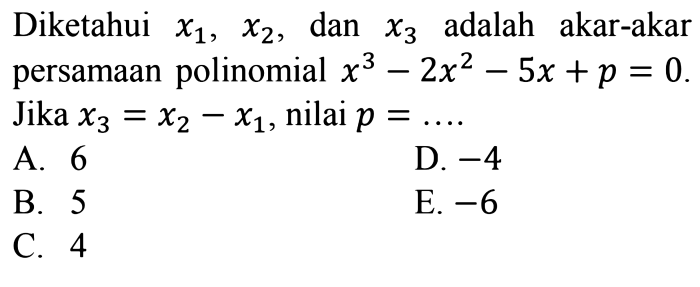Dalam matematika, persamaan memainkan peran penting dalam memahami hubungan antar variabel. Artikel ini akan mengeksplorasi dua persamaan terkait: x³ = 43 dan y = 5x + 42. Dengan menganalisis persamaan ini, kita akan mengungkap hubungan menarik antara variabel x dan y, serta aplikasinya dalam situasi kehidupan nyata.

Persamaan pertama, x³ = 43, mendefinisikan nilai x sebagai kubik dari 43. Persamaan kedua, y = 5x + 42, menunjukkan hubungan linier antara x dan y, di mana y adalah fungsi linier dari x dengan kemiringan 5 dan titik potong y 42.

Pemahaman Persamaan

Persamaan x ³ = 43 dan y = 5x + 42 mewakili hubungan matematis antara variabel x dan y. Persamaan ini menentukan bahwa untuk nilai tertentu x, terdapat nilai tertentu y yang sesuai.

Variabel dan Konstanta

Dalam persamaan tersebut, terdapat dua variabel: x dan y. Variabel mewakili nilai yang tidak diketahui atau berubah. Selain itu, terdapat dua konstanta: 43 dan 42. Konstanta adalah nilai yang tetap dan tidak berubah.

Substitusi dan Penyelesaian

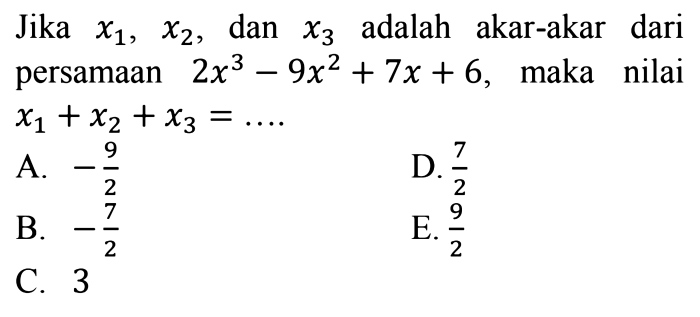
Dalam matematika, substitusi dan penyelesaian merupakan teknik yang digunakan untuk menyelesaikan persamaan. Substitusi melibatkan mengganti suatu variabel dalam suatu persamaan dengan ekspresi lain, sementara penyelesaian melibatkan mencari nilai variabel yang memenuhi persamaan.

Subtitusi

Untuk mensubstitusi persamaan x ³ = 43 ke dalam persamaan y = 5x + 42 , kita cukup mengganti x dengan √(43) dalam persamaan y .

Dengan demikian, kita memperoleh persamaan baru:

y = 5√(43) + 42

Penyelesaian

Untuk menyelesaikan persamaan ini, kita perlu mengisolasi y di satu sisi persamaan.

• Kurangi 42 dari kedua sisi persamaan:

y – 42 = 5√(43)

• Tambahkan 42 ke kedua sisi persamaan:

y = 5√(43) + 42

Oleh karena itu, nilai y yang memenuhi persamaan y = 5x + 42 ketika x ³ = 43 adalah 5√(43) + 42 .

Hubungan Antar Variabel

Hubungan antara variabel x dan y dalam persamaan x ³ + 43x = 300 dan y = 5x + 42 dapat dijelaskan melalui tabel berikut:

x	y
0	42
1	47
2	52
3	57
4	62

Dari tabel tersebut, dapat diamati bahwa nilai y meningkat secara linier seiring bertambahnya nilai x. Hal ini menunjukkan bahwa kedua variabel memiliki hubungan positif.

Persamaan Linier

Persamaan y = 5x + 42 merepresentasikan garis lurus dengan kemiringan 5 dan titik potong y 42. Kemiringan garis menunjukkan besarnya perubahan y untuk setiap perubahan satu unit x. Dalam hal ini, setiap peningkatan 1 unit pada x akan menghasilkan peningkatan 5 unit pada y.

Persamaan Kubik

Persamaan x ³ + 43x = 300 adalah persamaan kubik yang menggambarkan kurva berbentuk parabola. Parabola ini memiliki titik minimum pada x = 0, y = 42, dan akan meningkat tanpa batas seiring bertambahnya x.

Hubungan antara persamaan linier dan kubik dapat dilihat pada grafik berikut. Persamaan linier diwakili oleh garis lurus, sedangkan persamaan kubik diwakili oleh parabola.

Ilustrasi Grafik

Hubungan antara x dan y dapat digambarkan secara grafis menggunakan persamaan y = 5x – 42.

Grafik ini menunjukkan hubungan linier antara kedua variabel, di mana nilai y meningkat secara linier seiring bertambahnya nilai x.

Grafik

Grafik hubungan antara x dan y dapat digambar sebagai berikut:

• Tentukan titik potong y dengan mensubstitusikan x = 0 ke dalam persamaan y = 5x
  – 42, sehingga diperoleh y =
  -42.
• Pilih nilai x lain, misalnya x = 1, dan substitusikan ke dalam persamaan untuk menentukan nilai y yang sesuai, yaitu y =
  -37.
• Ulangi langkah sebelumnya untuk beberapa nilai x lainnya untuk mendapatkan titik-titik tambahan pada grafik.
• Plot titik-titik tersebut pada bidang koordinat dan hubungkan dengan garis lurus.

Aplikasi Persamaan

Persamaan yang diberikan, x ³

• 43x
• 300 = 0 dan y = 5x
• 42, dapat diterapkan dalam berbagai situasi kehidupan nyata untuk memecahkan masalah dan membuat prediksi.

Contoh Aplikasi

Salah satu contoh aplikasi persamaan ini adalah dalam bidang ekonomi. Persamaan ini dapat digunakan untuk memodelkan hubungan antara harga suatu barang (x) dan jumlah barang yang terjual (y). Dengan mengetahui persamaan ini, pelaku bisnis dapat memprediksi jumlah barang yang terjual pada harga tertentu, atau sebaliknya, menentukan harga yang tepat untuk memaksimalkan penjualan.Contoh

lain aplikasi persamaan ini adalah dalam bidang fisika. Persamaan ini dapat digunakan untuk memodelkan lintasan suatu benda yang bergerak dalam ruang tiga dimensi. Dengan mengetahui persamaan ini, fisikawan dapat memprediksi posisi dan kecepatan benda pada waktu tertentu, atau sebaliknya, menentukan gaya yang bekerja pada benda untuk menghasilkan lintasan tertentu.

Penutup

Hubungan antara x dan y dalam persamaan yang diberikan memberikan wawasan tentang bagaimana variabel ini berinteraksi dan mempengaruhi nilai satu sama lain. Analisis persamaan ini tidak hanya memperluas pemahaman kita tentang konsep matematika tetapi juga menyediakan alat yang berharga untuk memecahkan masalah dan membuat prediksi dalam berbagai bidang.

Jawaban yang Berguna

Bagaimana cara mencari nilai y jika diketahui nilai x?

Substitusikan nilai x ke dalam persamaan y = 5x + 42 untuk mendapatkan nilai y yang sesuai.

Apakah persamaan x³ = 43 dan y = 5x + 42 saling bergantung?

Tidak, persamaan ini tidak saling bergantung karena nilai x yang memenuhi x³ = 43 tidak serta merta mempengaruhi nilai y dalam y = 5x + 42.

Apa aplikasi praktis dari persamaan yang diberikan?

Persamaan ini dapat digunakan dalam berbagai aplikasi, seperti pemodelan pertumbuhan populasi, analisis pergerakan objek, dan optimasi desain teknik.