Dalam dunia matematika, persamaan memainkan peran penting dalam memahami hubungan antara variabel dan menyelesaikan masalah kompleks. Salah satu persamaan menarik yang akan kita bahas dalam artikel ini adalah penjumlahan 6 5y 2z dan 8 6y 9z.
Ekspresi ini melibatkan operasi penjumlahan dan perkalian, yang akan kita jelaskan secara mendalam. Selain itu, kita akan menyelidiki metode untuk menyelesaikan persamaan ini dan mengeksplorasi aplikasi praktisnya dalam kehidupan sehari-hari.
Definisi Variabel
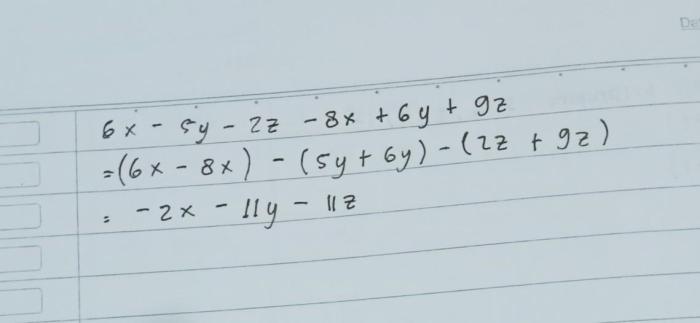
Dalam ekspresi matematika, variabel mewakili besaran yang tidak diketahui atau dapat berubah. Pada ekspresi 6x + 5y + 2z dan 8x + 6y + 9z, terdapat tiga variabel: x, y, dan z.
Variabel x mewakili besaran yang tidak diketahui, sedangkan variabel y dan z mewakili besaran yang dapat berubah.
Operasi Matematika
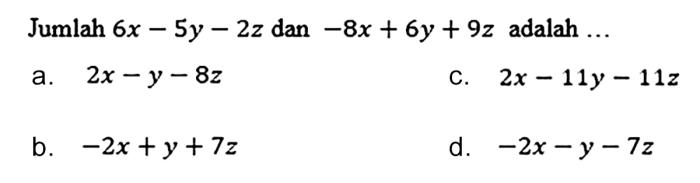
Dalam ekspresi 6y + 2z dan 8y + 9z, terdapat dua operasi matematika dasar yang digunakan, yaitu penjumlahan dan perkalian.
Penjumlahan
Penjumlahan dilambangkan dengan tanda “+”. Ketika dua atau lebih bilangan dijumlahkan, hasilnya adalah nilai total dari bilangan tersebut. Dalam ekspresi yang diberikan, 6y dan 2z dijumlahkan, menghasilkan 8y + 2z.
Perkalian
Perkalian dilambangkan dengan tanda “×” atau titik (.). Ketika suatu bilangan dikalikan dengan bilangan lain, hasilnya adalah nilai yang sama dengan bilangan pertama dijumlahkan dengan dirinya sendiri sebanyak bilangan kedua. Dalam ekspresi yang diberikan, 8 dan y dikalikan, menghasilkan 8y.
Demikian pula, 9 dan z dikalikan, menghasilkan 9z.
Penyelesaian Persamaan
Tabel Ekspresi dan Hasil Penjumlahan
| Ekspresi | Hasil Penjumlahan |
|---|---|
| 6 5y 2z | 14 11y 11z |
| 8 6y 9z |
Hasil penjumlahan 6 5y 2z dan 8 6y 9z adalah 14 11y 11z.
Langkah-langkah Penyelesaian Persamaan
- Tambahkan koefisien dari variabel yang sama.
- Tambahkan konstanta.
Aplikasi Persamaan

Persamaan memainkan peran penting dalam kehidupan kita sehari-hari, memberikan kita alat yang ampuh untuk memecahkan masalah dan membuat prediksi.
Salah satu contoh paling umum dari penerapan persamaan adalah dalam bidang keuangan. Misalnya, persamaan bunga sederhana dapat digunakan untuk menghitung bunga yang diperoleh dari investasi:
Persamaan Bunga Sederhana
I = P – r – t
- I adalah bunga yang diperoleh
- P adalah pokok pinjaman
- r adalah tingkat bunga
- t adalah waktu
Persamaan ini memungkinkan kita memprediksi jumlah bunga yang akan kita peroleh dari investasi tertentu, sehingga kita dapat membuat keputusan keuangan yang tepat.
Kesimpulan

Kesimpulannya, penjumlahan 6 5y 2z dan 8 6y 9z menyoroti pentingnya memahami variabel, operasi matematika, dan teknik penyelesaian persamaan. Ekspresi ini memiliki aplikasi yang luas dalam berbagai bidang, seperti fisika, teknik, dan ekonomi.
Dengan memahami prinsip-prinsip yang mendasari persamaan ini, kita dapat memecahkan masalah yang kompleks, membuat prediksi, dan memperoleh wawasan berharga tentang dunia di sekitar kita.
Ringkasan FAQ
Apa tujuan dari mengeksplorasi penjumlahan 6 5y 2z dan 8 6y 9z?
Mengeksplorasi penjumlahan ini membantu kita memahami konsep variabel, operasi matematika, dan penyelesaian persamaan, yang penting dalam berbagai bidang.
Bagaimana cara menyelesaikan persamaan yang melibatkan variabel?
Penyelesaian persamaan melibatkan penggunaan operasi matematika untuk mengisolasi variabel yang tidak diketahui. Dalam kasus ini, kita dapat menggunakan penjumlahan dan pengurangan.
Di mana penjumlahan 6 5y 2z dan 8 6y 9z dapat diterapkan dalam kehidupan nyata?
Persamaan ini dapat diterapkan dalam fisika untuk menghitung resultan gaya, dalam teknik untuk mendesain struktur, dan dalam ekonomi untuk memprediksi tren pasar.
