Dalam geometri, kedudukan titik dan garis terhadap lingkaran merupakan konsep mendasar yang memiliki aplikasi luas dalam kehidupan sehari-hari. Dari arsitektur hingga teknik, memahami hubungan ini sangat penting untuk memecahkan masalah dan merancang struktur yang efisien.

Artikel ini akan membahas berbagai posisi titik dan garis relatif terhadap lingkaran, menjelaskan sifat-sifat uniknya, dan menyajikan contoh penerapan praktisnya.

Definisi dan Konsep Dasar

Dalam geometri, titik, garis, dan lingkaran merupakan konsep dasar yang saling terkait.

Titikadalah sebuah lokasi dalam ruang yang tidak memiliki dimensi panjang, lebar, atau tinggi. Titik seringkali dilambangkan dengan huruf kapital, seperti A atau B.

Garisadalah sekumpulan titik yang terhubung dan memanjang tanpa henti ke dua arah. Garis dapat dilambangkan dengan huruf kecil, seperti latau m.

Dalam geometri, kedudukan titik dan garis terhadap lingkaran dapat diklasifikasikan menjadi berbagai jenis. Seperti yang kita ketahui, sistem koloid adalah campuran heterogen yang terdiri dari dua fase yang tidak saling larut, di mana salah satu fase terdispersi dalam fase lainnya.

Yang bukan merupakan sistem koloid adalah campuran homogen yang tidak memiliki fase terdispersi atau fase pendispersi yang berbeda. Kembali ke kedudukan titik dan garis terhadap lingkaran, hubungan spasial ini menentukan apakah titik atau garis berada di dalam, di luar, atau menyinggung lingkaran.

Lingkaranadalah sekumpulan titik yang jaraknya sama dari sebuah titik tetap yang disebut pusat. Lingkaran dapat dilambangkan dengan huruf kapital, seperti Oatau P, diikuti dengan simbol lingkaran, seperti Oatau P.

Hubungan antara titik, garis, dan lingkaran dapat digambarkan sebagai berikut:

• Titik dapat terletak pada garis.
• Titik dapat terletak di dalam, di luar, atau pada lingkaran.
• Garis dapat bersinggungan dengan lingkaran di satu atau dua titik.
• Garis dapat melalui pusat lingkaran.

Posisi Titik terhadap Lingkaran

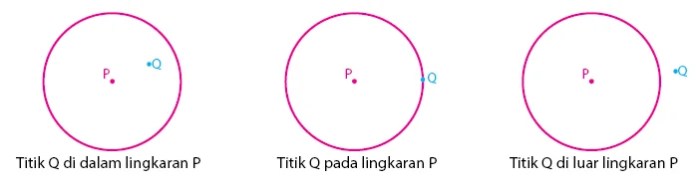
Posisi suatu titik relatif terhadap lingkaran dapat diklasifikasikan menjadi tiga kategori utama: di dalam lingkaran, di luar lingkaran, dan pada lingkaran.

Titik di Dalam Lingkaran

Sebuah titik dikatakan berada di dalam lingkaran jika jarak titik tersebut ke pusat lingkaran lebih kecil dari jari-jari lingkaran. Jarak ini dikenal sebagai jarak titik ke pusat.

Titik di Luar Lingkaran

Sebuah titik dikatakan berada di luar lingkaran jika jarak titik tersebut ke pusat lingkaran lebih besar dari jari-jari lingkaran.

Kedudukan titik dan garis terhadap lingkaran dapat menentukan hubungan geometris yang penting. Misalnya, titik yang berada di luar lingkaran disebut titik eksterior, sedangkan titik yang berada di dalam lingkaran disebut titik interior. Seperti halnya dalam cikalong , seni bela diri tradisional Sunda, posisi tubuh dan gerakan yang tepat sangat menentukan efektivitas teknik yang dilakukan.

Demikian pula, dalam geometri, kedudukan titik dan garis terhadap lingkaran dapat mempengaruhi sifat dan karakteristik hubungan geometris yang terbentuk.

Titik pada Lingkaran

Sebuah titik dikatakan berada pada lingkaran jika jarak titik tersebut ke pusat lingkaran sama dengan jari-jari lingkaran. Titik-titik ini membentuk batas lingkaran.

Tabel Posisi Titik terhadap Lingkaran

Posisi Titik	Hubungan dengan Lingkaran
Di dalam lingkaran	Jarak titik ke pusat < jari-jari lingkaran
Di luar lingkaran	Jarak titik ke pusat > jari-jari lingkaran
Pada lingkaran	Jarak titik ke pusat = jari-jari lingkaran

Posisi Garis terhadap Lingkaran: Kedudukan Titik Dan Garis Terhadap Lingkaran

Posisi garis terhadap lingkaran dapat diidentifikasi berdasarkan sifat interaksinya dengan lingkaran. Garis dapat memotong, menyinggung, atau sejajar dengan lingkaran.

Garis Memotong Lingkaran

Garis memotong lingkaran jika garis tersebut berpotongan dengan lingkaran di dua titik yang berbeda. Titik potong ini disebut titik potong garis dan lingkaran.

Garis Menyinggung Lingkaran

Garis menyinggung lingkaran jika garis tersebut berpotongan dengan lingkaran di satu titik saja. Titik potong ini disebut titik singgung garis dan lingkaran. Garis singgung selalu tegak lurus dengan jari-jari lingkaran yang ditarik dari titik singgung.

Garis Sejajar dengan Lingkaran

Garis sejajar dengan lingkaran jika garis tersebut tidak berpotongan dengan lingkaran pada titik mana pun. Jarak antara garis dan titik pusat lingkaran tetap konstan.

Kedudukan titik dan garis terhadap lingkaran dapat menentukan hubungan geometris yang berbeda. Misalnya, suatu titik dapat berada di dalam, di luar, atau pada lingkaran. Demikian pula, suatu garis dapat memotong, menyinggung, atau tidak berpotongan dengan lingkaran. Pemahaman tentang kedudukan ini sangat penting dalam bidang matematika, seperti pre-test , yang digunakan untuk mengukur pengetahuan atau keterampilan awal siswa sebelum proses pembelajaran dimulai.

Kembali ke kedudukan titik dan garis terhadap lingkaran, pemahaman yang baik tentang konsep ini dapat membantu memecahkan masalah dan memahami sifat-sifat geometris yang terkait.

Sifat Garis Tangent dan Garis Sekan

Garis singgung dan garis sekan merupakan garis-garis yang memiliki sifat unik dalam hubungannya dengan lingkaran.

Garis Singgung

Garis singgung pada lingkaran adalah garis yang hanya memiliki satu titik potong dengan lingkaran. Titik potong ini disebut titik singgung.

Sifat-sifat unik garis singgung:

• Tegak lurus dengan jari-jari yang ditarik ke titik singgung.
• Membagi sudut yang dibentuk oleh dua jari-jari yang ditarik dari titik pusat lingkaran ke titik-titik potong antara garis singgung dan lingkaran.

Garis Sekan, Kedudukan titik dan garis terhadap lingkaran

Garis sekan pada lingkaran adalah garis yang memotong lingkaran di dua titik yang berbeda. Panjang garis sekan sama dengan jarak antara kedua titik potong tersebut.

Sifat-sifat garis sekan:

• Membagi sudut yang dibentuk oleh dua jari-jari yang ditarik dari titik pusat lingkaran ke titik-titik potong antara garis sekan dan lingkaran menjadi dua bagian yang sama besar.
• Memiliki panjang yang lebih pendek dari garis singgung yang ditarik dari titik yang sama di luar lingkaran.

Aplikasi dalam Kehidupan Nyata

Konsep kedudukan titik dan garis terhadap lingkaran memiliki berbagai aplikasi praktis dalam berbagai bidang kehidupan.

Dalam teknik, konsep ini digunakan untuk:

Analisis Geometri

• Menentukan jarak titik dari lingkaran.
• Menentukan posisi garis yang bersinggungan dengan lingkaran.
• Menghitung luas daerah yang dibatasi oleh garis dan lingkaran.

Desain

• Membuat bentuk estetis dan fungsional yang melibatkan lingkaran.
• Menentukan posisi elemen desain dalam kaitannya dengan lingkaran.
• Menciptakan ilusi optik dan efek visual.

Arsitektur

• Merencanakan struktur bangunan dengan lengkungan dan kubah.
• Menentukan posisi jendela dan pintu dalam kaitannya dengan dinding bundar.
• Membuat desain interior yang estetis dan praktis.

Ringkasan Terakhir

Memahami kedudukan titik dan garis terhadap lingkaran tidak hanya memperluas pengetahuan geometris kita tetapi juga memberikan alat penting untuk memecahkan masalah dan merancang solusi inovatif dalam berbagai bidang.

Pertanyaan dan Jawaban

Apa itu garis singgung pada lingkaran?

Garis singgung adalah garis yang hanya menyentuh lingkaran di satu titik, dan tegak lurus dengan jari-jari yang ditarik ke titik tersebut.

Bagaimana menentukan apakah sebuah garis memotong lingkaran?

Sebuah garis memotong lingkaran jika jarak dari titik pusat lingkaran ke garis lebih kecil dari jari-jari lingkaran.