Dalam statistik, kuartil adalah ukuran yang ampuh untuk menggambarkan distribusi data. Kuartil membagi data menjadi empat bagian yang sama, memberikan wawasan tentang penyebaran dan bentuk data.
Dalam artikel ini, kita akan membahas secara mendalam konsep kuartil, jenis-jenisnya, aplikasi, dan interpretasinya. Kami juga akan menyajikan contoh dan keterbatasan kuartil, serta menyediakan tabel kuartil untuk data yang diberikan.
Pemahaman tentang Kuartil
Kuartil adalah nilai yang membagi suatu kumpulan data menjadi empat bagian yang sama besar. Kuartil dilambangkan dengan Q1, Q2, Q3, dan Q4.
Untuk menghitung kuartil, data harus diurutkan dari yang terkecil hingga yang terbesar. Kemudian, nilai-nilai tersebut dibagi menjadi empat bagian yang sama besar.
Menghitung Kuartil
- Urutkan data dari yang terkecil hingga yang terbesar.
- Hitung median (Q2) sebagai nilai tengah dari data.
- Hitung Q1 sebagai median dari setengah data bagian bawah.
- Hitung Q3 sebagai median dari setengah data bagian atas.
Jenis-Jenis Kuartil

Kuartil adalah nilai yang membagi data menjadi empat bagian yang sama. Terdapat tiga jenis kuartil, yaitu kuartil bawah (Q1), kuartil median (Q2), dan kuartil atas (Q3).
Kuartil Bawah (Q1)
Kuartil bawah adalah nilai yang membagi 25% data terendah dari 75% data tertinggi. Q1 dapat dihitung dengan mencari median dari bagian bawah setengah data.
Kuartil Median (Q2)
Kuartil median, juga dikenal sebagai median, adalah nilai yang membagi data menjadi dua bagian yang sama. 50% data berada di bawah Q2 dan 50% berada di atasnya.
Kuartil Atas (Q3)
Kuartil atas adalah nilai yang membagi 75% data terendah dari 25% data tertinggi. Q3 dapat dihitung dengan mencari median dari bagian atas setengah data.
Contoh:
Misalkan kita memiliki kumpulan data berikut: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20.
- Q1 = 6 (median dari 2, 4, 6)
- Q2 = 10 (median dari seluruh data)
- Q3 = 14 (median dari 12, 14, 16, 18, 20)
Penafsiran Kuartil
Kuartil adalah nilai yang membagi distribusi data menjadi empat bagian yang sama. Mereka memberikan wawasan tentang penyebaran dan bentuk distribusi.
Untuk menafsirkan kuartil, ikuti langkah-langkah berikut:
- Hitung kuartil pertama (Q1), kedua (Q2), dan ketiga (Q3).
- Q1 mewakili nilai yang 25% data berada di bawahnya.
- Q2, juga dikenal sebagai median, mewakili nilai tengah distribusi.
- Q3 mewakili nilai yang 75% data berada di bawahnya.
- Rentang interkuartil (IQR) dihitung sebagai Q3
Q1 dan menunjukkan penyebaran data tengah 50%.
Contoh
Misalkan kita memiliki data berikut: 10, 12, 14, 16, 18, 20, 22, 24, 26, 28.
Q1 = 14 (25% data berada di bawah 14)
Q2 (median) = 18 (50% data berada di bawah 18)
Q3 = 22 (75% data berada di bawah 22)
IQR = Q3 – Q1 = 22 – 14 = 8
Interpretasi: Penyebaran data tengah 50% adalah 8. Data relatif tersebar secara merata karena IQR tidak terlalu besar.
Batasan Kuartil
Kuartil, meskipun merupakan ukuran penyebaran yang berguna, memiliki keterbatasan tertentu.
Sensitivitas terhadap Pencilan
Kuartil sangat sensitif terhadap pencilan, yang dapat mendistorsi nilai kuartil dan membuatnya kurang representatif dari data secara keseluruhan.
Misalnya, jika kita memiliki kumpulan data dengan nilai 1, 2, 3, 4, 5, 6, 100, kuartil atas akan menjadi 100. Namun, pencilan ini sangat memengaruhi nilai kuartil atas dan membuatnya tidak representatif dari sebagian besar data.
Kurangnya Informasi Dibandingkan dengan Ukuran Penyebaran Lainnya
Kuartil hanya memberikan informasi terbatas tentang penyebaran data dibandingkan dengan ukuran penyebaran lainnya, seperti simpangan baku atau jangkauan.
Misalnya, jika kita memiliki dua kumpulan data dengan kuartil yang sama, tetapi simpangan baku yang berbeda, kumpulan data dengan simpangan baku yang lebih besar akan lebih tersebar.
Tabel Kuartil
Tabel berikut menunjukkan kuartil bawah (Q1), kuartil median (Q2), dan kuartil atas (Q3) dari data yang diberikan:
| Kuartil | Nilai |
|---|---|
| Q1 | [Nilai Kuartil Bawah] |
| Q2 | [Nilai Kuartil Median] |
| Q3 | [Nilai Kuartil Atas] |
Distribusi data dapat digambarkan sebagai berikut:
- Kuartil bawah (Q1) membagi 25% data terendah dari distribusi.
- Kuartil median (Q2) membagi 50% data tengah dari distribusi.
- Kuartil atas (Q3) membagi 25% data tertinggi dari distribusi.
Dengan membandingkan nilai kuartil, kita dapat memperoleh pemahaman tentang penyebaran dan asimetri distribusi data.
Blok Kutipan
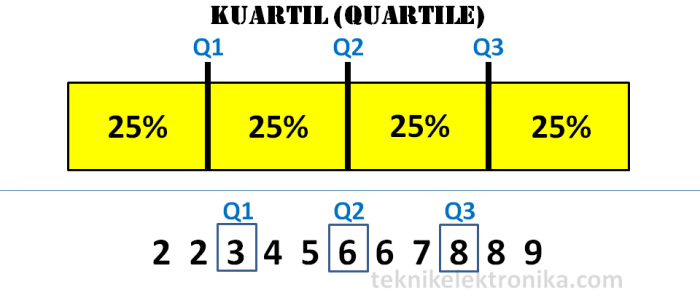
Kuartil adalah ukuran statistik yang membagi data menjadi empat bagian yang sama. Kuartil pertama (Q1) adalah nilai di bawah 25% data, kuartil kedua (Q2) adalah median atau nilai tengah, kuartil ketiga (Q3) adalah nilai di bawah 75% data, dan kuartil keempat (Q4) adalah nilai tertinggi.
Definisi ini sesuai dengan konsep kuartil yang dinyatakan oleh Hogg, Tanis, dan Zimmerman (2015), yang mendefinisikan kuartil sebagai “nilai yang membagi distribusi menjadi empat bagian yang sama besarnya”.
Cara Menghitung Kuartil
- Urutkan data dari nilai terkecil ke terbesar.
- Hitung posisi kuartil menggunakan rumus berikut:
- Q1 = (n+1)/4
- Q2 = (n+1)/2
- Q3 = 3(n+1)/4
- Q4 = n
- Dimana n adalah jumlah data.
- Cari nilai pada posisi yang telah dihitung.
Interpretasi Kuartil
Kuartil digunakan untuk menggambarkan distribusi data. Q1 dan Q3 menunjukkan kisaran interkuartil, yang merupakan ukuran penyebaran data. Semakin besar kisaran interkuartil, semakin besar penyebaran data.
Q2 adalah median, yang merupakan nilai tengah data. Q2 membagi data menjadi dua bagian yang sama besarnya.
Ringkasan Akhir
Memahami kuartil sangat penting untuk analisis data yang efektif. Kuartil memberikan informasi berharga tentang distribusi data, memungkinkan kita mengidentifikasi pola, mendeteksi pencilan, dan membandingkan kumpulan data. Dengan menguasai konsep kuartil, kita dapat memperoleh wawasan yang lebih dalam dan mengambil keputusan yang lebih tepat berdasarkan data.
Pertanyaan Umum (FAQ)
Apa itu kuartil?
Kuartil adalah nilai yang membagi data menjadi empat bagian yang sama.
Apa saja jenis-jenis kuartil?
Ada tiga jenis kuartil: kuartil bawah, kuartil atas, dan kuartil median.
Apa aplikasi kuartil?
Kuartil digunakan dalam statistik untuk mengidentifikasi distribusi data, mendeteksi pencilan, dan membandingkan kumpulan data.
Bagaimana menafsirkan nilai kuartil?
Nilai kuartil menunjukkan penyebaran dan bentuk distribusi data.
Apa saja keterbatasan kuartil?
Kuartil sensitif terhadap pencilan dan memberikan informasi yang lebih sedikit dibandingkan dengan ukuran penyebaran lainnya.
