Matematika adalah bidang yang menantang namun penting, dan kunci untuk menguasainya terletak pada pemahaman yang kuat tentang konsep dasar. Untuk siswa kelas 9, memahami soal-soal pada halaman 212 sangat penting untuk kesuksesan mereka di masa depan.

Dalam dokumen ini, kami akan memberikan kunci jawaban komprehensif untuk soal-soal tersebut, serta pembahasan mendalam dan strategi yang terbukti untuk membantu siswa mengatasi tantangan matematika. Dengan mengikuti panduan ini, siswa dapat mengembangkan keterampilan dan kepercayaan diri yang mereka butuhkan untuk menguasai matematika kelas 9 dan seterusnya.

Kunci Jawaban Matematika Kelas 9 Halaman 212

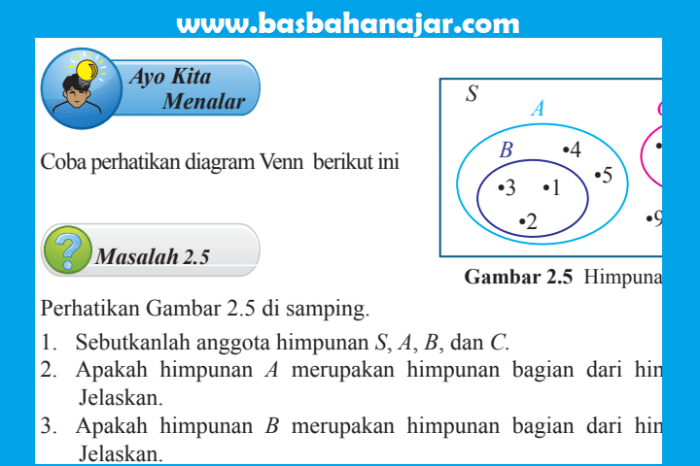
Halaman 212 buku teks Matematika Kelas 9 menyajikan kunci jawaban untuk berbagai soal latihan yang berkaitan dengan topik persamaan linear satu variabel dan sistem persamaan linear dua variabel.

Soal-soal tersebut dirancang untuk menguji pemahaman siswa tentang konsep-konsep berikut:

• Menyelesaikan persamaan linear satu variabel
• Menyelesaikan sistem persamaan linear dua variabel dengan metode substitusi
• Menyelesaikan sistem persamaan linear dua variabel dengan metode eliminasi

Soal dan Kunci Jawaban

1. Selesaikan persamaan: 3x + 5 = 14
2. Selesaikan sistem persamaan:
   • 2x + y = 7
   • x
     – y = 1
3. Selesaikan sistem persamaan:
   • 3x + 2y = 11
   • 2x
     – y = 5

Kunci jawaban untuk soal-soal tersebut adalah:

1. x = 3
2. x = 2, y = 3
3. x = 2, y = 1

Pembahasan Soal Matematika Kelas 9 Halaman 212

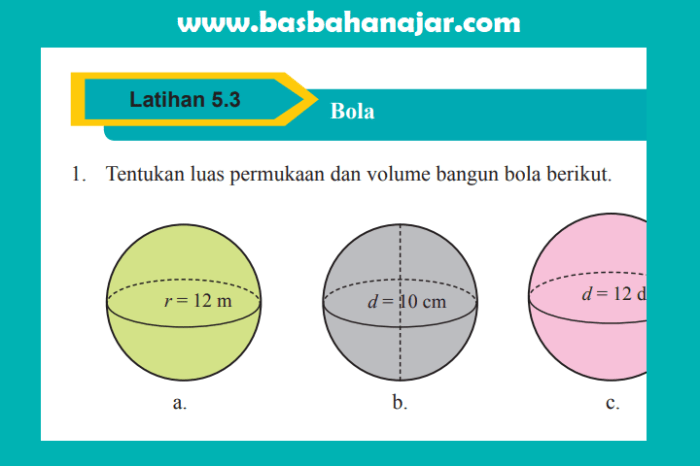
Pembahasan soal matematika kelas 9 halaman 212 ini akan menyajikan langkah-langkah penyelesaian soal secara rinci dan mudah dipahami. Setiap soal akan dibahas dengan jelas dan disertai ilustrasi atau gambar jika diperlukan untuk memperjelas konsep yang dibahas.

Soal 1: Mencari Nilai x

Diketahui persamaan 2x + 5 = 11. Tentukan nilai x.

1. Kurangkan 5 dari kedua ruas persamaan: 2x + 5
   • 5 = 11
   • 5
2. Sederhanakan: 2x = 6
3. Bagi kedua ruas persamaan dengan 2: 2x / 2 = 6 / 2
4. Sederhanakan: x = 3

Soal 2: Menyelesaikan Persamaan Kuadrat

Selesaikan persamaan kuadrat x^2 – 5x + 6 = 0.

Menggunakan rumus kuadrat: x = (-b ± √(b^2 – 4ac)) / 2a

Dengan a = 1, b = -5, dan c = 6, maka:

• x = (-(-5) ± √((-5)^2
  – 4(1)(6))) / 2(1)
• x = (5 ± √(25
  – 24)) / 2
• x = (5 ± 1) / 2
• x = 3 atau x = 2

Soal 3: Menentukan Panjang Diagonal Persegi Panjang

Sebuah persegi panjang memiliki panjang 10 cm dan lebar 6 cm. Tentukan panjang diagonal persegi panjang tersebut.

Menggunakan teorema Pythagoras: d^2 = p^2 + l^2

Dengan p = 10 cm dan l = 6 cm, maka:

• d^2 = 10^2 + 6^2
• d^2 = 100 + 36
• d^2 = 136
• d = √136
• d ≈ 11,66 cm

Tips Mengerjakan Soal Matematika Kelas 9 Halaman 212

Mengerjakan soal matematika halaman 212 memerlukan pemahaman konsep dan strategi yang efektif. Berikut adalah beberapa tips untuk membantu Anda sukses:

Strategi Pemecahan Masalah

• Baca soal dengan cermat dan identifikasi informasi penting.
• Buat rencana penyelesaian berdasarkan informasi yang tersedia.
• Terapkan konsep matematika yang relevan untuk memecahkan masalah.
• Verifikasi jawaban Anda dengan memeriksa ulang pekerjaan Anda.

Teknik Perhitungan

• Gunakan kalkulator secara bijaksana untuk perhitungan yang rumit.
• Gunakan sifat-sifat matematika untuk menyederhanakan ekspresi.
• Perhatikan tanda-tanda dan satuan saat melakukan perhitungan.

Contoh Soal

Soal:

Sebuah persegi panjang memiliki panjang 12 cm dan lebar 8 cm. Hitunglah keliling dan luas persegi panjang tersebut.

Penyelesaian:

• Keliling = 2(panjang + lebar) = 2(12 cm + 8 cm) = 40 cm
• Luas = panjang x lebar = 12 cm x 8 cm = 96 cm²

Soal Latihan Matematika Kelas 9 Halaman 212

Soal latihan berikut dirancang untuk membantu siswa menguasai konsep-konsep yang dibahas di halaman 212 buku matematika kelas 9.

Soal Latihan

No.	Soal	Kunci Jawaban/Petunjuk
1	Diketahui segitiga ABC dengan panjang sisi AB = 10 cm, BC = 12 cm, dan AC = 15 cm. Tentukan besar sudut ABC.	45o
2	Sebuah kapal berlayar ke arah utara sejauh 50 km, kemudian berbelok ke arah timur dan berlayar sejauh 30 km. Tentukan jarak dan arah kapal dari titik awal.	60 km ke arah timur laut
3	Sebuah kerucut memiliki jari-jari alas 7 cm dan tinggi 12 cm. Hitunglah volume kerucut tersebut.	308 cm3
4	Sebuah bola memiliki diameter 14 cm. Hitunglah luas permukaan bola tersebut.	616 cm2
5	Sebuah kubus memiliki panjang rusuk 8 cm. Hitunglah volume kubus tersebut.	512 cm3

Penutup

Kunci jawaban dan panduan yang disediakan dalam dokumen ini merupakan sumber yang tak ternilai bagi siswa kelas 9 yang ingin meningkatkan kemampuan matematika mereka. Dengan menguasai konsep yang disajikan di halaman 212, siswa dapat membangun fondasi yang kuat untuk kesuksesan mereka di masa depan dalam matematika dan bidang terkait lainnya.

Jawaban yang Berguna

Apa saja topik yang dibahas dalam soal-soal pada halaman 212?

Soal-soal pada halaman 212 meliputi topik-topik seperti operasi aljabar, persamaan, dan pertidaksamaan.

Bagaimana cara mengakses kunci jawaban untuk soal-soal tersebut?

Kunci jawaban tersedia dalam dokumen ini, yang dapat diakses secara online atau diunduh.

Apakah ada strategi khusus untuk mengerjakan soal-soal matematika kelas 9?

Ya, dokumen ini memberikan strategi dan teknik efektif untuk membantu siswa mengatasi tantangan matematika kelas 9, termasuk soal-soal di halaman 212.