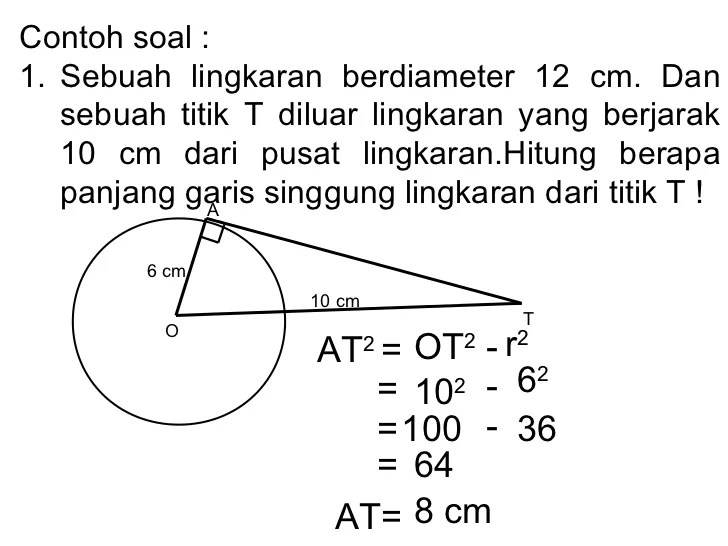
Persamaan lingkaran merupakan konsep fundamental dalam matematika, terutama pada tingkat kelas 11. Pemahaman yang mendalam tentang persamaan ini sangat penting untuk menyelesaikan berbagai permasalahan yang melibatkan geometri dan aljabar. Artikel ini akan memberikan panduan komprehensif mengenai latihan soal persamaan lingkaran, meliputi bentuk umum, pusat, jari-jari, pengubahan bentuk, dan sifat-sifat lingkaran.

Dengan menguasai topik ini, siswa akan memperoleh kemampuan analitis dan pemahaman spasial yang lebih baik, serta mempersiapkan diri untuk studi matematika tingkat lanjut dan aplikasi dalam berbagai bidang seperti teknik, fisika, dan astronomi.

Persamaan Lingkaran Kelas 11

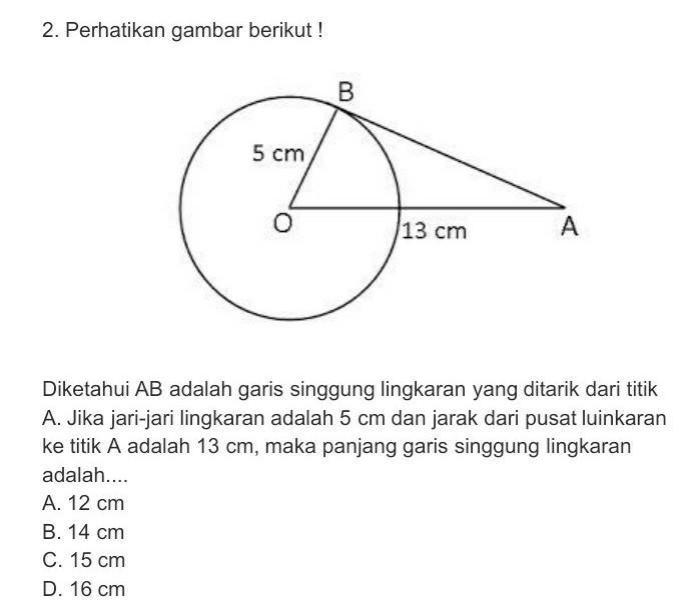
Persamaan lingkaran adalah persamaan matematika yang mendefinisikan sebuah lingkaran di bidang koordinat. Persamaan ini menggambarkan hubungan antara jarak setiap titik pada lingkaran ke pusat lingkaran, yang disebut jari-jari.

Bentuk Umum Persamaan Lingkaran

Persamaan umum persamaan lingkaran adalah:

(x

• h)² + (y
• k)² = r²

di mana:

• (h, k) adalah koordinat pusat lingkaran
• r adalah jari-jari lingkaran

Contoh Persamaan Lingkaran

• (x
  – 2)² + (y + 3)² = 49
• Lingkaran dengan pusat di (2,
  -3) dan jari-jari 7
• x² + y² = 25
• Lingkaran dengan pusat di (0, 0) dan jari-jari 5

Bentuk Umum Persamaan Lingkaran

Persamaan lingkaran dalam bentuk umum dinyatakan sebagai (x – h)^2 + (y – k)^2 = r^2, di mana (h, k) adalah pusat lingkaran dan r adalah jari-jarinya.

Pusat Lingkaran

Pusat lingkaran (h, k) adalah titik tengah lingkaran. Jarak dari setiap titik pada lingkaran ke pusat adalah sama dengan jari-jari.

Jari-jari Lingkaran

Jari-jari lingkaran (r) adalah jarak dari pusat ke setiap titik pada lingkaran. Jari-jari menentukan ukuran lingkaran.

Menentukan Pusat dan Jari-jari Lingkaran

Persamaan lingkaran umumnya dinyatakan dalam bentuk:

(x

• h)² + (y
• k)² = r²

di mana (h, k) adalah pusat lingkaran dan r adalah jari-jarinya.

Langkah-langkah Menentukan Pusat dan Jari-jari Lingkaran

1. Bandingkan persamaan lingkaran dengan bentuk umum.
2. Tentukan nilai h dan k dari koefisien kuadrat (x
   • h)² dan (y
   • k)².
3. Tentukan nilai r dari koefisien konstan r².

Contoh

Persamaan Lingkaran	Pusat (h, k)	Jari-jari (r)
x² + y² 4x + 6y 12 = 0	(2, 3)	5
(x + 1)² + (y 2)² = 9	(-1, 2)	3
2x² + 2y² 8x + 12y 18 = 0	(2, 3)	3

Mengubah Bentuk Persamaan Lingkaran

Persamaan lingkaran dapat dinyatakan dalam berbagai bentuk, termasuk bentuk umum dan bentuk standar. Mengubah persamaan lingkaran dari bentuk umum ke bentuk standar sangat penting untuk berbagai operasi geometri, seperti mencari pusat dan jari-jari lingkaran.

Mengubah Persamaan Lingkaran ke Bentuk Standar

Untuk mengubah persamaan lingkaran dari bentuk umum (Ax ² + By ² + Cx + Dy + E = 0) ke bentuk standar (x ² + y ² + Dx + Ey + F = 0), ikuti langkah-langkah berikut:

1. Bagi persamaan dengan A, sehingga persamaan menjadi x² + (B/A)y² + (C/A)x + (D/A)y + (E/A) = 0.
2. Lengkapkan kuadrat pada x dan y. Untuk x, tambahkan dan kurangkan (C/2A)², dan untuk y, tambahkan dan kurangkan (D/2B)².
3. Sederhanakan persamaan untuk mendapatkan persamaan dalam bentuk standar x² + y² + Dx + Ey + F = 0.

Contoh

Misalkan kita memiliki persamaan lingkaran 2x ² + 3y ² – 4x + 6y – 1 = 0. Untuk mengubahnya ke bentuk standar:

• Bagi persamaan dengan 2: x² + (3/2)y²
  – 2x + 3y
  – 1/2 = 0
• Lengkapkan kuadrat: x²
  – 2x + 1 + (3/2)y² + 3y + 9/8
  – 1/2
  – 1 = 0
• Sederhanakan: (x
  – 1)² + (3/2)(y + 3/4)² = 1/8

Persamaan lingkaran dalam bentuk standar adalah (x – 1) ² + (3/2)(y + 3/4) ² = 1/8.

Persamaan Lingkaran yang Memotong Sumbu Koordinat

Persamaan lingkaran yang memotong sumbu koordinat memiliki karakteristik khusus yang membedakannya dari persamaan lingkaran pada umumnya. Ketika sebuah lingkaran memotong sumbu koordinat, artinya lingkaran tersebut bersinggungan dengan kedua sumbu x dan y.

Kondisi Persamaan Lingkaran yang Memotong Sumbu Koordinat

• Lingkaran memotong sumbu x di dua titik yang berbeda.
• Lingkaran memotong sumbu y di dua titik yang berbeda.
• Jarak dari pusat lingkaran ke sumbu x sama dengan jarak dari pusat lingkaran ke sumbu y.

Jika sebuah lingkaran memiliki persamaan x^2 + y^2 + 2gx + 2fy + c = 0 , maka lingkaran tersebut memotong sumbu koordinat jika dan hanya jika g^2 + f^2 = c .

Menentukan Persamaan Lingkaran dari Sifat-sifatnya

Persamaan lingkaran dapat ditentukan dari sifat-sifatnya, seperti pusat dan jari-jari atau titik-titik yang dilaluinya. Berikut langkah-langkah untuk menentukan persamaan lingkaran berdasarkan sifat-sifat tersebut:

Menentukan Persamaan Lingkaran jika Diketahui Pusat dan Jari-jari

• Tentukan pusat lingkaran sebagai titik (h, k).
• Tentukan jari-jari lingkaran sebagai r.
• Gunakan persamaan lingkaran umum: (x
  – h)² + (y
  – k)² = r².

Menentukan Persamaan Lingkaran jika Diketahui Titik-titik yang Dilaluinya

Jika diketahui tiga titik yang dilalui lingkaran, maka persamaan lingkaran dapat ditentukan dengan:

1. Mencari pusat lingkaran menggunakan rumus:
   

   (h, k) = ((x₁ + x₃) / 2, (y₁ + y₃) / 2)

   di mana (x₁, y₁) dan (x₃, y₃) adalah dua titik yang diketahui.

2. Menghitung jari-jari lingkaran menggunakan rumus jarak:
   

   r = √((x₁

   • h)² + (y₁
   • k)²)

di mana (x₁, y₁) adalah salah satu titik yang diketahui.

3. Menggunakan persamaan lingkaran umum: (x
   • h)² + (y
   • k)² = r².

Kesimpulan

Melalui latihan soal yang terstruktur dan pemahaman yang mendalam tentang konsep persamaan lingkaran, siswa akan meningkatkan keterampilan berpikir kritis dan pemecahan masalah mereka.

Topik ini tidak hanya penting untuk kemajuan akademik, tetapi juga memberikan dasar yang kuat untuk aplikasi praktis dalam berbagai disiplin ilmu.

Pertanyaan dan Jawaban

Apa pentingnya mempelajari persamaan lingkaran di kelas 11?

Mempelajari persamaan lingkaran sangat penting untuk mengembangkan pemahaman spasial, keterampilan analitis, dan persiapan untuk studi matematika tingkat lanjut dan aplikasi dalam berbagai bidang.

Apa saja bentuk umum persamaan lingkaran?

(x – h)^2 + (y – k)^2 = r^2, di mana (h, k) adalah pusat dan r adalah jari-jari lingkaran.

Bagaimana cara menentukan pusat dan jari-jari lingkaran dari persamaannya?

Pusat: (h, k); Jari-jari: r

Apa saja sifat-sifat lingkaran yang memotong sumbu koordinat?

Memotong sumbu x: D = 2h; Memotong sumbu y: E = 2k