Latihan soal sudut pusat dan sudut keliling – Dalam geometri, sudut pusat dan sudut keliling memainkan peran penting dalam menentukan sifat-sifat lingkaran. Latihan soal yang terkait dengan topik ini sangat penting untuk memahami konsep-konsep dasar dan menerapkannya dalam menyelesaikan masalah geometri.

Latihan soal sudut pusat dan sudut keliling mencakup berbagai aspek, mulai dari definisi dan rumus hingga teorema dan aplikasi praktis. Dengan mengerjakan soal-soal ini, siswa dapat mempertajam pemahaman mereka tentang topik tersebut dan mengembangkan keterampilan berpikir kritis mereka.

Definisi

Dalam geometri, sudut pusat dan sudut keliling adalah dua jenis sudut yang terkait dengan lingkaran.

Sudut pusat adalah sudut yang terbentuk oleh dua jari-jari lingkaran, sedangkan sudut keliling adalah sudut yang terbentuk oleh dua garis singgung lingkaran yang ditarik dari titik yang sama pada lingkaran.

Perbedaan antara Sudut Pusat dan Sudut Keliling

• Sudut pusatdiukur oleh busur yang dicegatnya, sedangkan sudut kelilingdiukur oleh setengah busur yang dicegatnya.
• Sudut pusatselalu sama dengan setengah dari sudut kelilingyang mencegat busur yang sama.
• Sudut pusatterletak di dalam lingkaran, sedangkan sudut kelilingterletak di luar lingkaran.

Rumus dan Properti

Rumus untuk menghitung sudut pusat dan sudut keliling adalah sebagai berikut:

• Sudut pusat = (360°/n)°, di mana n adalah jumlah sisi poligon
• Sudut keliling = (180°-2n)°, di mana n adalah jumlah sisi poligon

Sifat-sifat sudut pusat dan sudut keliling antara lain:

Sifat Sudut Pusat, Latihan soal sudut pusat dan sudut keliling

• Sudut pusat suatu poligon beraturan sama besar.
• Sudut pusat suatu poligon beraturan sebanding dengan jumlah sisi poligon tersebut.

Sifat Sudut Keliling

• Sudut keliling suatu poligon beraturan sama besar.
• Sudut keliling suatu poligon beraturan berbanding terbalik dengan jumlah sisi poligon tersebut.

Teorema dan Bukti

Dalam geometri, terdapat teorema penting yang mengaitkan besar sudut pusat dan sudut keliling dalam suatu lingkaran. Teorema-teorema ini memberikan hubungan yang mendasar antara sudut-sudut yang terbentuk oleh tali busur, garis singgung, dan pusat lingkaran.

Teorema Sudut Pusat

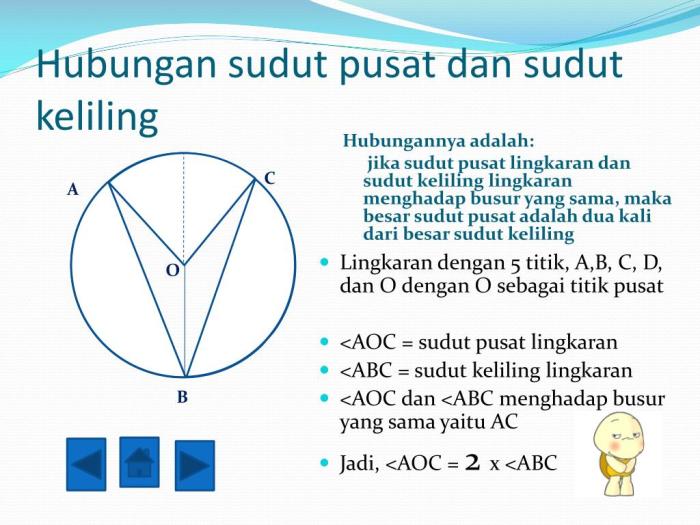
Teorema Sudut Pusat menyatakan bahwa besar sudut pusat suatu lingkaran sama dengan dua kali besar sudut keliling yang menghadangnya pada tali busur yang sama.

Dengan kata lain, jika ∠O adalah sudut pusat dan ∠PQR adalah sudut keliling yang menghadapinya pada tali busur PQ, maka ∠O = 2∠PQR.

Teorema Sudut Keliling

Teorema Sudut Keliling menyatakan bahwa besar sudut keliling suatu lingkaran sama dengan setengah besar sudut pusat yang menghadapinya pada tali busur yang sama.

Dengan kata lain, jika ∠PQR adalah sudut keliling dan ∠O adalah sudut pusat yang menghadapinya pada tali busur PQ, maka ∠PQR = 1/2 ∠O.

Bukti Teorema Sudut Pusat

Bukti Teorema Sudut Pusat dapat diperoleh menggunakan prinsip kesebangunan segitiga. Perhatikan segitiga OPR dan segitiga OPQ yang terbentuk oleh sudut pusat ∠O dan sudut keliling ∠PQR.

Segitiga OPR dan OPQ sebangun karena memiliki sudut yang sama di titik P. Oleh karena itu, perbandingan sisi-sisi yang bersesuaian adalah sama.

Dalam hal ini, perbandingan OP/PR = OP/OQ. Mengingat OP = OQ (jari-jari lingkaran), maka PR = OQ.

Dengan demikian, ∠PQR = ∠ORP, karena kedua sudut tersebut merupakan sudut yang berhadapan dengan sisi yang sama panjang.

Namun, ∠ORP adalah setengah dari ∠O (karena OP adalah garis bagi sudut ∠O). Oleh karena itu, ∠PQR = 1/2 ∠O, atau ∠O = 2∠PQR.

Latihan soal sudut pusat dan sudut keliling menguji pemahaman siswa tentang konsep geometri. Sementara itu, perusahaan goods dikenal dengan perusahaan yang memproduksi barang-barang konsumen berkualitas tinggi, menunjukkan pentingnya pemahaman matematika dalam dunia bisnis. Latihan soal sudut pusat dan sudut keliling mempersiapkan siswa untuk penerapan konsep matematika dalam berbagai bidang, termasuk desain produk dan pengembangan teknologi yang diproduksi oleh perusahaan seperti ini.

Bukti Teorema Sudut Keliling

Bukti Teorema Sudut Keliling dapat diperoleh sebagai konsekuensi dari Teorema Sudut Pusat. Jika ∠O = 2∠PQR, maka ∠PQR = 1/2 ∠O.

Contoh Soal dan Solusi

Berikut beberapa contoh soal latihan sudut pusat dan sudut keliling beserta solusi lengkapnya:

Soal 1

Dalam sebuah lingkaran dengan jari-jari 10 cm, sebuah busur memiliki panjang 15 cm. Hitunglah besar sudut pusat dan sudut keliling yang terbentuk oleh busur tersebut.

Solusi:

• Sudut pusat:

Sudut pusat = (Panjang busur / Keliling lingkaran) x 360 derajat

Sudut pusat = (15 cm / (2π x 10 cm)) x 360 derajat

Sudut pusat = 27 derajat

• Sudut keliling:

Sudut keliling = (Sudut pusat / 2) derajat

Dalam menyelesaikan latihan soal sudut pusat dan sudut keliling, pemahaman yang baik tentang konsep-konsep tersebut sangat penting. Salah satu cara untuk memperkuat pemahaman adalah dengan menerapkan prinsip-prinsip metode ilmiah. Metode ilmiah, seperti yang diilustrasikan dalam contoh metode ilmiah tentang tumbuhan tomat , melibatkan pengamatan, pembentukan hipotesis, pengujian, dan penarikan kesimpulan.

Dengan menerapkan prinsip-prinsip ini pada latihan soal sudut pusat dan sudut keliling, siswa dapat mengembangkan pemahaman yang lebih mendalam tentang topik tersebut.

Sudut keliling = (27 derajat / 2) derajat

Sudut keliling = 13,5 derajat

Soal 2

Sebuah sektor lingkaran memiliki sudut pusat 60 derajat. Jika panjang jari-jari sektor tersebut adalah 8 cm, hitunglah luas dan keliling sektor tersebut.

Solusi:

• Luas sektor:

Luas sektor = (Sudut pusat / 360 derajat) x Luas lingkaran

Luas sektor = (60 derajat / 360 derajat) x π x 8 cm ²

Luas sektor = 34,56 cm²

• Keliling sektor:

Keliling sektor = Panjang busur + 2 x Panjang jari-jari

Keliling sektor = (60 derajat / 360 derajat) x 2π x 8 cm + 2 x 8 cm

Keliling sektor = 24,6 cm

Aplikasi dalam Geometri

Sudut pusat dan sudut keliling memainkan peran penting dalam geometri, memberikan dasar untuk memahami sifat dan pengukuran bentuk geometri.

Latihan soal sudut pusat dan sudut keliling dapat mengasah kemampuan geometri. Namun, terkadang keadaan tak terduga mengharuskan kita absen dari suatu acara, seperti pernikahan. Dalam situasi tersebut, mengirimkan ucapan maaf tidak bisa hadir ke pernikahan yang tulus menjadi bentuk apresiasi dan rasa hormat.

Ucapan maaf tersebut dapat mencakup alasan ketidakhadiran, harapan baik, dan ucapan selamat kepada pasangan yang menikah. Dengan demikian, kita dapat menjaga hubungan baik meski tidak dapat menghadiri acara tersebut. Setelah mengucapkan maaf, penting untuk kembali fokus pada latihan soal sudut pusat dan sudut keliling untuk memperdalam pemahaman geometri.

Pengukuran Sudut dalam Lingkaran

• Sudut pusat mengukur busur lingkaran yang dijepit oleh dua jari-jari, sedangkan sudut keliling mengukur busur lingkaran yang dijepit oleh dua tali busur.
• Teorema sudut pusat menyatakan bahwa besar sudut pusat sama dengan setengah besar busur yang dijepit.
• Teorema sudut keliling menyatakan bahwa besar sudut keliling sama dengan setengah jumlah besar sudut pusat yang dijepit.

Aplikasi dalam Desain Arsitektur

• Sudut pusat digunakan untuk menentukan ukuran dan bentuk lengkungan, kubah, dan struktur melingkar lainnya.
• Sudut keliling digunakan untuk mengukur dan merancang sudut jendela, pintu, dan elemen arsitektur lainnya.

Aplikasi dalam Navigasi

• Sudut pusat digunakan untuk mengukur sudut antara dua titik pada peta atau kompas.
• Sudut keliling digunakan untuk mengukur sudut antara dua titik pada permukaan bumi.

Latihan Tambahan

Latihan tambahan ini akan membantu Anda memperkuat pemahaman tentang sudut pusat dan sudut keliling lingkaran.

Soal Latihan

• Sebuah lingkaran memiliki jari-jari 10 cm. Hitunglah besar sudut pusat yang menghadap busur lingkaran sepanjang 6 cm.
• Sebuah busur lingkaran memiliki panjang 24 cm. Jika jari-jari lingkaran adalah 12 cm, hitunglah besar sudut keliling yang menghadap busur tersebut.
• Sebuah lingkaran memiliki sudut pusat 60 derajat. Jika jari-jari lingkaran adalah 8 cm, hitunglah panjang busur yang menghadap sudut tersebut.
• Sebuah busur lingkaran memiliki panjang 18 cm. Jika sudut keliling yang menghadap busur tersebut adalah 45 derajat, hitunglah jari-jari lingkaran.

Penutupan Akhir

Secara keseluruhan, latihan soal sudut pusat dan sudut keliling sangat penting untuk menguasai konsep-konsep dasar geometri. Dengan berlatih soal-soal ini secara teratur, siswa dapat meningkatkan kemampuan mereka dalam menyelesaikan masalah dan mempersiapkan diri dengan baik untuk ujian dan tugas matematika di masa depan.

Informasi FAQ: Latihan Soal Sudut Pusat Dan Sudut Keliling

Apa itu sudut pusat?

Sudut pusat adalah sudut yang terbentuk oleh dua jari-jari lingkaran yang berpotongan di pusat lingkaran.

Bagaimana cara menghitung sudut keliling?

Sudut keliling adalah sudut yang terbentuk oleh dua garis singgung yang berpotongan pada lingkaran. Besar sudut keliling sama dengan setengah dari sudut pusat yang menghadap busur yang sama.

Apa saja aplikasi sudut pusat dan sudut keliling dalam geometri?

Sudut pusat dan sudut keliling digunakan dalam berbagai aplikasi geometri, seperti menentukan panjang busur, luas juring, dan sifat-sifat segitiga istimewa.