Dalam dunia matematika, limit fungsi tak hingga memegang peran penting dalam memahami perilaku fungsi trigonometri saat argumennya mendekati tak hingga. Konsep ini memungkinkan kita untuk mengungkap perilaku asimtotik fungsi-fungsi tersebut, yang sangat penting dalam berbagai aplikasi.
Limit fungsi tak hingga trigonometri memberikan wawasan tentang bagaimana fungsi trigonometri mendekati nilai tertentu saat sudutnya bertambah besar atau mengecil tak terhingga. Memahami konsep ini sangat penting untuk menguasai kalkulus dan bidang matematika terkait lainnya.
Batas Fungsi Trigonometri Tak Hingga
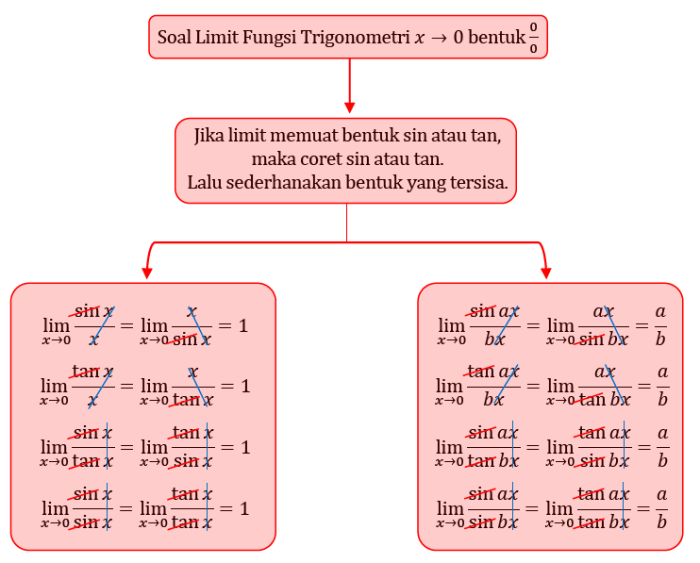
Ketika argumen fungsi trigonometri mendekati tak hingga, nilai fungsinya sering kali memiliki perilaku tertentu. Perilaku ini dapat dipelajari menggunakan konsep limit fungsi trigonometri tak hingga.
Limit fungsi trigonometri tak hingga adalah nilai yang didekati oleh fungsi trigonometri saat argumennya mendekati tak hingga. Misalnya, limit dari sinus x saat x mendekati tak hingga adalah 1.
Limit Fungsi Trigonometri Tak Hingga Umum
Berikut adalah tabel yang merangkum limit umum fungsi trigonometri tak hingga:
| Fungsi | Limit Saat x
|
|---|---|
| sin(x) | Tidak ada limit |
| cos(x) | Tidak ada limit |
| tan(x) | Tidak ada limit |
| cot(x) | 0 |
| sec(x) | 1 |
| csc(x) | 1 |
Teknik Menghitung Limit Fungsi Trigonometri Tak Hingga
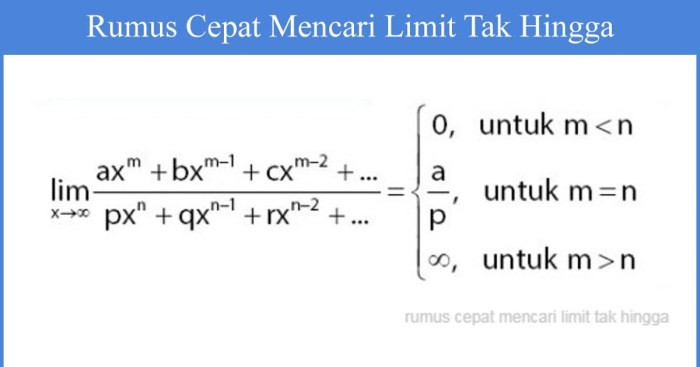
Dalam matematika, menghitung limit fungsi trigonometri tak hingga sangat penting untuk memahami perilaku fungsi trigonometri saat argumennya mendekati tak hingga.
Ada beberapa teknik yang dapat digunakan untuk menghitung limit ini.
Teknik Substitusi Langsung
Teknik substitusi langsung melibatkan mensubstitusi nilai tak hingga ke dalam fungsi dan mengevaluasi hasilnya. Teknik ini hanya berlaku jika fungsi tidak memiliki bentuk tak tentu seperti 0/0 atau ∞/∞.
Teknik Faktorisasi
Teknik faktorisasi melibatkan memfaktorkan fungsi trigonometri menjadi bentuk yang lebih sederhana. Setelah difaktorkan, nilai tak hingga dapat disubstitusikan ke dalam setiap faktor untuk mengevaluasi limit.
Teknik Trigonometri Identitas
Teknik identitas trigonometri melibatkan penggunaan identitas trigonometri untuk mengubah fungsi menjadi bentuk yang lebih sederhana. Setelah diubah, teknik substitusi langsung atau faktorisasi dapat digunakan untuk mengevaluasi limit.
Teknik Hopital
Teknik Hopital digunakan untuk mengevaluasi limit bentuk tak tentu seperti 0/0 atau ∞/∞. Teknik ini melibatkan mengambil turunan dari pembilang dan penyebut fungsi dan kemudian mengevaluasi limitnya.
Langkah-langkah Menghitung Limit Fungsi Trigonometri Tak Hingga
- Tentukan bentuk tak tentu fungsi saat argumen mendekati tak hingga.
- Pilih teknik yang sesuai berdasarkan bentuk tak tentu.
- Substitusikan tak hingga ke dalam fungsi atau terapkan teknik yang dipilih.
- Evaluasi limitnya.
Aplikasi Limit Fungsi Trigonometri Tak Hingga
Limit fungsi trigonometri tak hingga memiliki aplikasi yang luas dalam matematika dan bidang lainnya. Aplikasi ini memungkinkan penyelesaian masalah yang melibatkan besaran yang sangat besar atau sangat kecil, seperti dalam kalkulus, fisika, dan teknik.
Aplikasi dalam Kalkulus
- Mencari turunan dan integral fungsi trigonometri.
- Mencari nilai limit dan asimtot fungsi trigonometri.
- Mengevaluasi integral tak tentu yang melibatkan fungsi trigonometri.
Aplikasi dalam Fisika
- Menganalisis gerakan periodik, seperti gerak osilasi dan gelombang.
- Menghitung gaya yang bekerja pada benda yang bergerak dalam medan magnet.
- Memodelkan fenomena akustik, seperti resonansi dan interferensi.
Aplikasi dalam Teknik
- Mendesain sirkuit elektronik yang melibatkan kapasitor dan induktor.
- Menganalisis stabilitas sistem kontrol.
- Memproses sinyal yang mengandung komponen frekuensi tinggi.
Ilustrasi Grafik Limit Fungsi Trigonometri Tak Hingga

Grafik fungsi trigonometri tak hingga memberikan representasi visual yang kuat dari konsep limit. Grafik ini menunjukkan bagaimana nilai fungsi trigonometri mendekati nilai tertentu saat argumen fungsi mendekati tak hingga.
Sebagai contoh, pertimbangkan fungsi trigonometri sinus (sin x). Saat x mendekati tak hingga, grafik fungsi sinus berosilasi antara -1 dan 1. Namun, amplitudo osilasi ini berkurang saat x semakin besar, mendekati 0. Grafik ini menunjukkan bahwa limit dari sin x saat x mendekati tak hingga adalah 0.
Grafik Limit Sinus dan Kosinus
- Grafik fungsi sinus (sin x) menunjukkan bahwa limit dari sin x saat x mendekati tak hingga adalah 0.
- Grafik fungsi kosinus (cos x) juga menunjukkan limit 0 saat x mendekati tak hingga.
Kutipan Ahli Matematika
“Limit fungsi trigonometri tak hingga sangat penting dalam matematika, karena menyediakan dasar untuk memahami konsep konvergensi dan divergensi deret tak hingga.”
Leonhard Euler
Penutupan
Limit fungsi tak hingga trigonometri terbukti menjadi alat yang sangat berharga dalam berbagai disiplin ilmu. Mereka menyediakan kerangka kerja untuk menganalisis perilaku fungsi trigonometri dalam skenario dunia nyata, seperti fisika, teknik, dan ilmu komputer. Dengan memanfaatkan teknik yang diuraikan dalam diskusi ini, para praktisi dapat memperoleh pemahaman yang lebih dalam tentang sifat fungsi trigonometri dan menerapkannya untuk menyelesaikan masalah yang kompleks.
Jawaban untuk Pertanyaan Umum
Apa perbedaan antara limit satu sisi dan dua sisi?
Limit satu sisi mendekati argumen dari satu arah (kiri atau kanan), sedangkan limit dua sisi mendekati argumen dari kedua arah sekaligus.
Mengapa limit fungsi trigonometri tak hingga penting?
Limit ini memungkinkan kita untuk menentukan perilaku fungsi saat argumennya menjadi sangat besar atau sangat kecil, yang berguna dalam menganalisis grafik fungsi dan menyelesaikan masalah aplikasi.
Bagaimana teknik substitusi digunakan untuk menghitung limit fungsi trigonometri tak hingga?
Dengan mensubstitusi nilai trigonometri tertentu (misalnya, sin(π/2) = 1) ke dalam fungsi, kita dapat mengevaluasi limitnya secara langsung.
