Dalam ranah matematika, limit memainkan peran penting dalam memahami perilaku fungsi saat variabelnya mendekati nilai tertentu. Dalam trigonometri, limit memegang signifikansi khusus, memberikan wawasan tentang sifat fungsi trigonometri ketika argumennya menjadi sangat besar.

Limit tak hingga dalam trigonometri menawarkan lensa unik untuk menyelidiki perilaku fungsi trigonometri ketika nilai argumennya mendekati tak terbatas. Pemahaman tentang limit tak hingga ini membuka pintu ke berbagai aplikasi dalam kalkulus, analisis fungsi, dan bidang terkait.

Limit Trigonometri

Dalam trigonometri, limit digunakan untuk menentukan nilai fungsi trigonometri saat sudutnya mendekati nilai tertentu atau tak hingga. Limit trigonometri penting dalam berbagai aplikasi, seperti kalkulus, analisis Fourier, dan fisika.

Beberapa contoh limit trigonometri umum adalah:

• lim (sin x) / x = 1 saat x mendekati 0
• lim (cos x
  – 1) / x = 0 saat x mendekati 0
• lim (tan x) = tak hingga saat x mendekati π/2 dari kanan

Properti Limit Trigonometri

Limit trigonometri memiliki beberapa properti penting, antara lain:

• Linieritas: Limit jumlah atau selisih fungsi trigonometri sama dengan jumlah atau selisih limit masing-masing fungsi.
• Produk dan Kuasien: Limit produk atau kuasien fungsi trigonometri sama dengan produk atau kuasien limit masing-masing fungsi.
• Komposisi: Limit komposisi fungsi trigonometri sama dengan komposisi limit masing-masing fungsi.
• Identitas Trigonometri: Limit identitas trigonometri sama dengan identitas yang sesuai.

Limit Tak Hingga

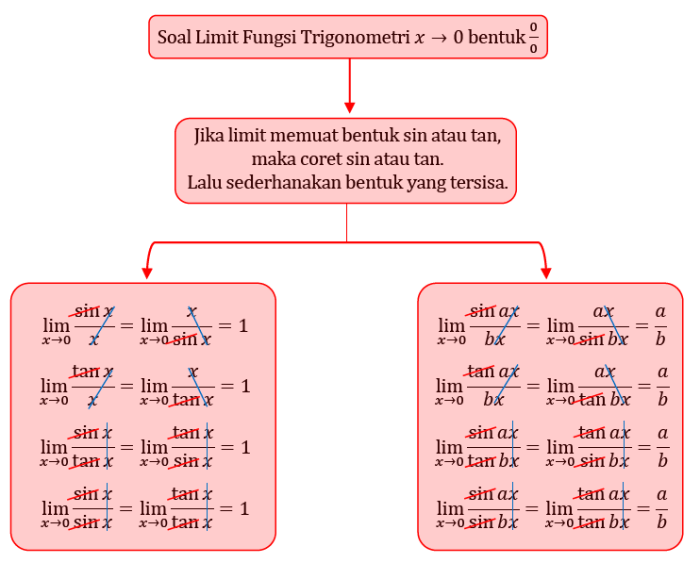
Dalam trigonometri, limit tak hingga mengacu pada perilaku fungsi trigonometri saat argumennya (sudut) mendekati nilai tak hingga.

Saat argumen mendekati tak hingga, beberapa fungsi trigonometri mendekati nilai tertentu, sementara yang lain berosilasi tanpa batas.

Limit Khusus

• Sin x: Saat x → ∞, sin x berosilasi antara
  -1 dan 1.
• Cos x: Saat x → ∞, cos x berosilasi antara
  -1 dan 1.
• Tan x: Saat x → ∞, tan x mendekati tak hingga.
• Cot x: Saat x → ∞, cot x mendekati nol.
• Sec x: Saat x → ∞, sec x berosilasi antara
  -1 dan 1.
• Csc x: Saat x → ∞, csc x berosilasi antara
  -1 dan 1.

Implikasi

Limit tak hingga dalam trigonometri memiliki implikasi penting:

• Menentukan perilaku grafik fungsi trigonometri pada nilai argumen yang sangat besar.
• Membantu menyelesaikan persamaan trigonometri dengan mengganti argumen tak hingga dengan nilai limitnya.
• Digunakan dalam kalkulus untuk menentukan turunan dan integral fungsi trigonometri.

Penerapan Limit Trigonometri

Limit trigonometri memainkan peran penting dalam kalkulus, analisis fungsi trigonometri, dan berbagai aplikasi lainnya.

Identifikasi Penerapan Limit Trigonometri dalam Kalkulus

Limit trigonometri digunakan untuk:* Mencari turunan fungsi trigonometri.

• Mengintegrasikan fungsi trigonometri.
• Menentukan limit fungsi trigonometri.

Berikan Contoh Penggunaan Limit Trigonometri untuk Menghitung Integral

Salah satu aplikasi penting limit trigonometri adalah dalam penghitungan integral. Misalnya, integral dari sin(x) dapat dihitung menggunakan limit:“`∫ sin(x) dx = lim (n→∞) [∑ (i=1 to n) sin(iπ/n)

(π/n)]

“`

Diskusikan Peran Limit Trigonometri dalam Analisis Fungsi Trigonometri

Limit trigonometri juga penting dalam analisis fungsi trigonometri. Dengan menggunakan limit, kita dapat:* Menentukan sifat-sifat fungsi trigonometri, seperti periodisitas, simetri, dan nilai limit.

• Mempelajari perilaku fungsi trigonometri pada tak hingga.
• Mengklasifikasikan fungsi trigonometri sebagai fungsi kontinu, diferensiabel, atau terintegrasi.

Tabel Limit Trigonometri

Dalam trigonometri, limit adalah nilai yang didekati oleh suatu fungsi trigonometri ketika variabelnya mendekati nilai tertentu. Berikut adalah tabel yang merangkum beberapa limit trigonometri umum:

Nilai Limit

• Limit: sin(x) / x

  Nilai Limit: 1

  Kondisi: x mendekati 0

• Limit: cos(x) – 1 / x^2

  Nilai Limit: -1/2

  Kondisi: x mendekati 0

• Limit: tan(x) / x

  Nilai Limit: 1

  Kondisi: x mendekati 0

• Limit: (1 – cos(x)) / x^2

  Nilai Limit: 1/2

  Kondisi: x mendekati 0

Prosedur Menghitung Limit Trigonometri

Menghitung limit trigonometri melibatkan teknik khusus untuk mengatasi ketidakpastian yang timbul saat variabel mendekati tak hingga atau suatu nilai tertentu. Langkah-langkah berikut menguraikan prosedur umum untuk menghitung limit trigonometri:

Substitusi

Jika batas fungsi trigonometri dapat ditentukan dengan langsung menggantikan nilai limit ke dalam fungsi, maka metode substitusi dapat digunakan. Misalnya, untuk menghitung lim _{x → 0} sin x , kita dapat langsung menggantikan x dengan 0:

lim _{x → 0} sin x = sin 0 = 0

Faktorisasi

Faktorisasi dapat digunakan untuk menyederhanakan ekspresi trigonometri sebelum mengevaluasi limit. Misalnya, untuk menghitung lim _{x → π/2} (1 – cos x) / sin x , kita dapat memfaktorkan pembilangnya:

(1 – cos x) / sin x = (sin x/2)(sin x/2) / sin x = sin x/2

Kemudian, kita dapat mengganti x dengan π/2 untuk mengevaluasi limit:

lim _{x → π/2} (1 – cos x) / sin x = lim _{x → π/2} sin x/2 = 1

Contoh Langkah Demi Langkah

Hitunglah lim _{x → 0} (tan x – x) / x ³ :

Langkah 1: Faktorkan pembilangnya:

(tan x – x) / x ³ = (sin x / cos x – x) / x ³

Langkah 2: Sederhanakan pembilangnya menggunakan identitas trigonometri:

(sin x / cos x – x) / x ³ = (sin x – x cos x) / (cos x x ³ )

Langkah 3: Substitusikan x dengan 0 untuk mengevaluasi limit:

lim _{x → 0} (tan x – x) / x ³ = lim _{x → 0} (sin x – x cos x) / (cos x x ³ ) = 0

Ilustrasi Limit Trigonometri

Limit fungsi trigonometri dapat divisualisasikan melalui grafik. Grafik ini menunjukkan bagaimana fungsi mendekati nilai tertentu saat argumennya mendekati tak hingga.

Untuk memahami konsep limit, perhatikan grafik fungsi sinus sebagai contoh. Saat argumen mendekati tak hingga, grafik berosilasi antara -1 dan 1, tidak pernah mencapai nilai tertentu.

Limit Fungsi Sinus

Ketika argumen fungsi sinus mendekati tak hingga, nilai fungsi berosilasi tanpa batas antara -1 dan 1. Ini menunjukkan bahwa limit fungsi sinus saat argumen mendekati tak hingga adalah tidak terdefinisi.

Limit Fungsi Kosinus

Sebaliknya, ketika argumen fungsi kosinus mendekati tak hingga, nilai fungsi berosilasi tanpa batas antara -1 dan 1. Namun, grafik fungsi kosinus tidak berpotongan dengan sumbu x. Ini menunjukkan bahwa limit fungsi kosinus saat argumen mendekati tak hingga adalah tidak terdefinisi.

Limit Fungsi Tangent

Fungsi tangen memiliki perilaku yang berbeda. Ketika argumen mendekati tak hingga, nilai fungsi mendekati garis vertikal. Ini menunjukkan bahwa limit fungsi tangen saat argumen mendekati tak hingga adalah tak hingga.

Penutupan

Dengan mengeksplorasi limit trigonometri, kita tidak hanya memperoleh pemahaman yang lebih dalam tentang fungsi trigonometri, tetapi juga membuka potensi penerapannya yang luas. Dari menghitung integral hingga menganalisis perilaku fungsi yang kompleks, limit trigonometri berfungsi sebagai alat yang sangat berharga bagi matematikawan, insinyur, dan ilmuwan.

Jawaban yang Berguna

Apa signifikansi limit tak hingga dalam trigonometri?

Limit tak hingga memberikan wawasan tentang perilaku fungsi trigonometri saat argumennya menjadi sangat besar, membantu kita memahami pola dan tren yang mungkin tidak terlihat pada nilai argumen yang lebih kecil.

Bagaimana limit trigonometri digunakan dalam kalkulus?

Limit trigonometri sangat penting dalam kalkulus untuk menghitung integral fungsi trigonometri. Dengan mengevaluasi limit tak hingga, kita dapat menentukan luas daerah di bawah kurva fungsi trigonometri.

Mengapa tabel limit trigonometri berguna?

Tabel limit trigonometri menyediakan referensi cepat untuk nilai limit umum, menghemat waktu dan usaha dalam perhitungan trigonometri yang kompleks.