Dalam geometri, luas irisan dua lingkaran merupakan konsep penting yang banyak diaplikasikan dalam berbagai bidang kehidupan. Artikel ini akan mengeksplorasi rumus perhitungan, faktor yang memengaruhi, penerapan, dan ilustrasi geometris dari luas irisan dua lingkaran.

Luas irisan dua lingkaran didefinisikan sebagai daerah yang tumpang tindih antara dua lingkaran. Perhitungannya melibatkan jari-jari dan jarak antar titik pusat kedua lingkaran.

Konsep Luas Irisan Dua Lingkaran

Luas irisan dua lingkaran adalah area yang tumpang tindih antara kedua lingkaran. Luas ini dapat dihitung menggunakan rumus berikut:

Luas Irisan = (1/2)

• (R1^2 + R2^2
• d^2)
• sin(2θ)

di mana:

• R1 dan R2 adalah jari-jari kedua lingkaran
• d adalah jarak antara titik pusat kedua lingkaran
• θ adalah setengah sudut irisan

Faktor yang Mempengaruhi Luas Irisan Dua Lingkaran

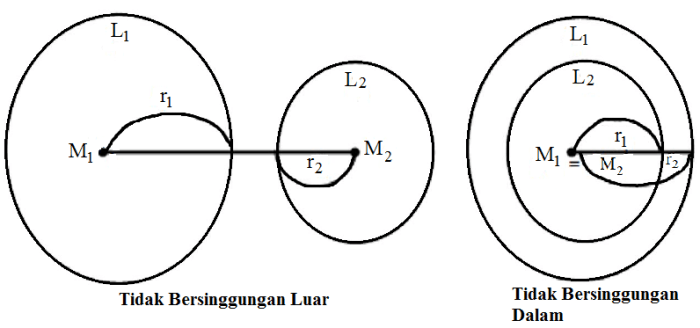
Luas irisan dua lingkaran dipengaruhi oleh beberapa faktor, terutama jari-jari dan titik pusat kedua lingkaran.

Jarak Antara Titik Pusat dan Jari-jari

Jarak antara titik pusat dua lingkaran (d) dan jari-jari kedua lingkaran (r1 dan r2) memainkan peran penting dalam menentukan luas irisan. Jika d > r1 + r2, kedua lingkaran tidak akan beririsan. Jika d< |r1 - r2|, kedua lingkaran akan beririsan pada dua titik dan luas irisannya akan menjadi nol. Jika d berada di antara r1 - r2 dan r1 + r2, kedua lingkaran akan beririsan pada dua titik dan luas irisannya akan lebih besar dari nol.

Penerapan Luas Irisan Dua Lingkaran

Luas irisan dua lingkaran memiliki berbagai penerapan dalam kehidupan nyata, terutama dalam bidang teknik dan desain. Berikut adalah beberapa contohnya:

Teknik

• Perhitungan luas tumpang tindih antara dua pipa atau kabel yang saling berpotongan.
• Desain sistem ventilasi untuk menentukan luas area tumpang tindih antara dua saluran udara.
• Perhitungan luas permukaan yang dibagikan oleh dua benda bulat, seperti roda gigi atau bantalan.

Desain

• Penentuan luas area tumpang tindih antara dua objek yang tumpang tindih, seperti jendela yang saling berdekatan.
• Perhitungan luas permukaan yang dibagikan oleh dua benda berbentuk lingkaran, seperti vas atau mangkuk.
• Desain pola atau motif dekoratif yang melibatkan lingkaran yang saling tumpang tindih.

Prosedur Menghitung Luas Irisan Dua Lingkaran

Menghitung luas irisan dua lingkaran melibatkan beberapa langkah berikut:

Mencari Jari-jari Lingkaran

Langkah pertama adalah mencari jari-jari kedua lingkaran, yang dilambangkan sebagai r1 dan r2.

Mencari Panjang Garis Singgung Persekutuan

Selanjutnya, cari panjang garis singgung persekutuan (l) antara kedua lingkaran. Garis singgung persekutuan adalah garis lurus yang menyinggung kedua lingkaran pada titik yang sama.

Mencari Sudut Pusat Lingkaran

Tentukan sudut pusat kedua lingkaran, yang dilambangkan sebagai θ1 dan θ2. Sudut pusat adalah sudut yang terbentuk oleh dua jari-jari yang menghubungkan titik pusat lingkaran dengan titik singgung.

Menghitung Luas Irisan

Terakhir, hitung luas irisan (A) menggunakan rumus berikut:

A = (1/2)

• (r1^2
• θ1 + r2^2
• θ2
• l^2
• sin(θ1 + θ2))

Dimana:

• r1 adalah jari-jari lingkaran pertama
• r2 adalah jari-jari lingkaran kedua
• θ1 adalah sudut pusat lingkaran pertama
• θ2 adalah sudut pusat lingkaran kedua
• l adalah panjang garis singgung persekutuan

Ilustrasi Geometris Luas Irisan Dua Lingkaran

Ilustrasi geometris dapat membantu memvisualisasikan konsep luas irisan dua lingkaran. Misalkan kita memiliki dua lingkaran dengan jari-jari r1 dan r2 yang berpotongan. Daerah yang dibentuk oleh perpotongan ini dikenal sebagai irisan lingkaran.

Untuk menghitung luas irisan, kita dapat membagi irisan menjadi dua segitiga dan satu segmen setengah lingkaran. Luas segitiga dapat dihitung menggunakan rumus 1/2 – alas – tinggi, sedangkan luas segmen setengah lingkaran dapat dihitung menggunakan rumus 1/2 – r^2 – θ, di mana θ adalah sudut pusat yang dibentuk oleh segmen tersebut.

Berikut adalah ilustrasi geometris dari luas irisan dua lingkaran:

• Dua lingkaran berjari-jari r1 dan r2 berpotongan pada titik A dan B.
• Irisan yang terbentuk dibagi menjadi dua segitiga, ΔABC dan ΔABD.
• Luas segitiga ΔABC = 1/2
  – AB
  – AC
• Luas segitiga ΔABD = 1/2
  – AB
  – AD
• Luas segmen setengah lingkaran dengan jari-jari r1 = 1/2
  – r1^2
  – θ1
• Luas segmen setengah lingkaran dengan jari-jari r2 = 1/2
  – r2^2
  – θ2

Dengan menambahkan luas segitiga dan segmen setengah lingkaran, kita dapat memperoleh rumus luas irisan dua lingkaran:

Luas Irisan = 1/2

• (r1^2
• θ1 + r2^2
• θ2) + AB
• (AC + AD)

Penutup

Memahami luas irisan dua lingkaran sangat penting dalam berbagai bidang, mulai dari teknik hingga desain. Dengan menguasai konsep ini, kita dapat memecahkan masalah yang kompleks dan merancang solusi yang optimal.

Jawaban yang Berguna

Apa rumus untuk menghitung luas irisan dua lingkaran?

Luas irisan = 1/2 x (R^2 x θ – r^2 x φ) – luas daerah tumpang tindih (jika ada)

Bagaimana jarak antar titik pusat memengaruhi luas irisan?

Semakin besar jarak antar titik pusat, semakin kecil luas irisannya.

Berikan contoh penerapan luas irisan dua lingkaran dalam kehidupan nyata.

Contohnya, dalam desain teknik, menghitung luas irisan dua roda gigi untuk menentukan rasio transmisi.