Bangun ruang merupakan bentuk tiga dimensi yang menempati ruang. Memahami berbagai jenis bangun ruang sangat penting dalam berbagai bidang, seperti matematika, arsitektur, dan teknik.

Dalam artikel ini, kita akan menjelajahi beragam jenis bangun ruang, mulai dari prisma hingga bola. Setiap jenis akan dibahas secara detail, dilengkapi dengan rumus volume dan gambar ilustrasinya.

Bangun Ruang

Bangun ruang adalah objek geometris tiga dimensi yang memiliki panjang, lebar, dan tinggi. Berbeda dengan bangun datar yang hanya memiliki dua dimensi, bangun ruang memiliki volume yang dapat dihitung.

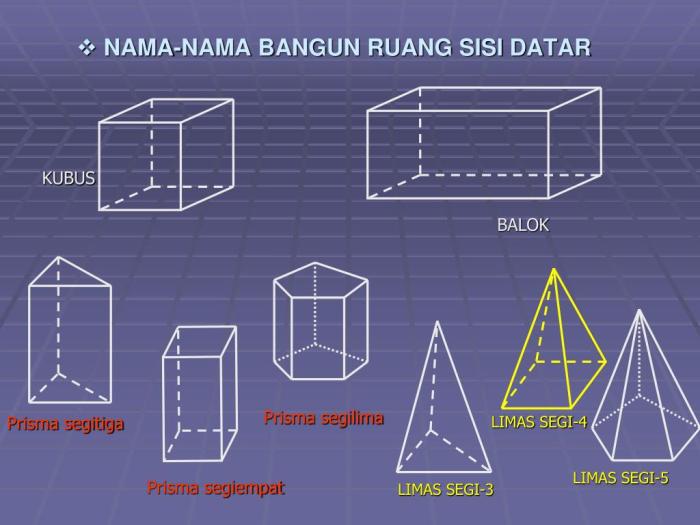
Bangun ruang dapat diklasifikasikan berdasarkan bentuknya, antara lain:

Prisma

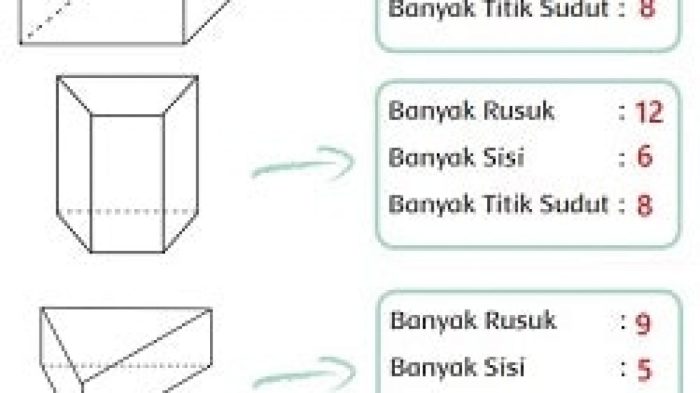
• Prisma adalah bangun ruang yang memiliki dua sisi sejajar dan kongruen yang disebut sisi alas dan sisi atas.
• Sisi-sisi lainnya berbentuk persegi panjang dan disebut sisi tegak.
• Jenis prisma antara lain prisma segitiga, prisma segi empat, dan prisma segi banyak.

Limas

• Limas adalah bangun ruang yang memiliki satu sisi alas berbentuk poligon dan sisi-sisi lainnya berbentuk segitiga yang bertemu pada satu titik yang disebut titik puncak.
• Jenis limas antara lain limas segitiga, limas segi empat, dan limas segi banyak.

Tabung

• Tabung adalah bangun ruang yang memiliki dua sisi alas berbentuk lingkaran yang sejajar dan kongruen.
• Sisi-sisi lainnya berbentuk persegi panjang dan disebut sisi tegak.

Kerucut

• Kerucut adalah bangun ruang yang memiliki satu sisi alas berbentuk lingkaran dan sisi lainnya berbentuk kerucut yang bertemu pada satu titik yang disebut titik puncak.

Bola

• Bola adalah bangun ruang yang memiliki semua titik pada permukaannya berjarak sama dari satu titik yang disebut titik pusat.

Jenis-Jenis Bangun Ruang

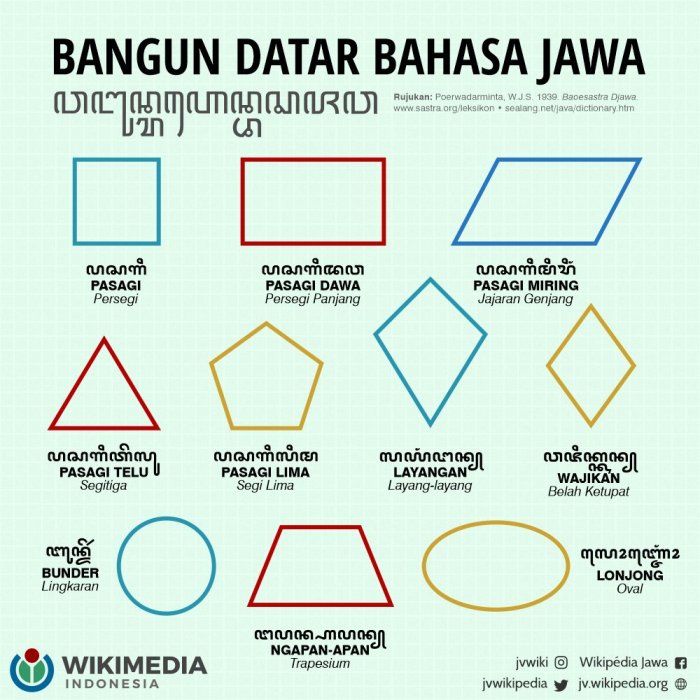
Bangun ruang merupakan bentuk tiga dimensi yang memiliki panjang, lebar, dan tinggi. Berbagai jenis bangun ruang memiliki sifat dan rumus volume yang berbeda-beda.

Kubus

• Rumus volume: V = s³
• Kubus memiliki 6 sisi persegi yang sama
• Semua sudut kubus adalah sudut siku-siku
• Diagonal ruang kubus sama dengan s√3

Balok

• Rumus volume: V = p × l × t
• Balok memiliki 6 sisi persegi panjang
• Balok memiliki 3 pasang sisi yang sejajar dan sama
• Diagonal ruang balok sama dengan √(p² + l² + t²)

Prisma

• Prisma memiliki 2 sisi sejajar dan kongruen yang disebut sisi alas dan sisi atas
• Sisi-sisi lainnya berbentuk persegi panjang
• Rumus volume prisma: V = Luas alas × tinggi

Limas

• Limas memiliki sebuah sisi yang berbentuk bidang datar (alas) dan sisi-sisi lainnya berbentuk segitiga
• Rumus volume limas: V = 1/3 × Luas alas × tinggi

Kerucut

• Kerucut memiliki sebuah sisi yang berbentuk lingkaran (alas) dan sebuah sisi yang berbentuk kerucut
• Rumus volume kerucut: V = 1/3 × πr² × t

Bola

• Bola memiliki bentuk yang bulat sempurna
• Rumus volume bola: V = 4/3 × πr³

Rumus Volume Bangun Ruang

Volume suatu bangun ruang merupakan besaran yang menyatakan banyaknya ruang yang ditempati oleh bangun ruang tersebut. Volume diukur dalam satuan kubik, seperti sentimeter kubik (cm³), meter kubik (m³), atau liter (L).

Rumus volume untuk setiap jenis bangun ruang berbeda-beda. Berikut adalah rumus volume untuk beberapa bangun ruang yang umum:

Kubus

• Rumus: V = s³
• Keterangan: V adalah volume, s adalah panjang rusuk kubus

Balok

• Rumus: V = p x l x t
• Keterangan: V adalah volume, p adalah panjang, l adalah lebar, t adalah tinggi

Prisma Segitiga

• Rumus: V = 1/2 x L x t x h
• Keterangan: V adalah volume, L adalah luas alas segitiga, t adalah tinggi segitiga, h adalah tinggi prisma

Limas Segitiga

• Rumus: V = 1/3 x L x h
• Keterangan: V adalah volume, L adalah luas alas segitiga, h adalah tinggi limas

Kerucut

• Rumus: V = 1/3 x π x r² x h
• Keterangan: V adalah volume, π adalah konstanta pi (3,14), r adalah jari-jari alas kerucut, h adalah tinggi kerucut

Bola

• Rumus: V = 4/3 x π x r³
• Keterangan: V adalah volume, π adalah konstanta pi (3,14), r adalah jari-jari bola

Untuk menghitung volume suatu bangun ruang, cukup substitusikan nilai panjang, lebar, tinggi, atau jari-jari yang sesuai ke dalam rumus volume. Hasilnya akan memberikan volume bangun ruang tersebut dalam satuan kubik.

4. Contoh Soal dan Pembahasan

Untuk memperdalam pemahaman tentang bangun ruang, berikut disajikan beberapa contoh soal latihan menghitung volume bangun ruang beserta pembahasannya.

Soal 1

Hitunglah volume kubus yang memiliki panjang rusuk 5 cm.

Pembahasan

Rumus volume kubus: V = s ³ Diketahui: s = 5 cmV = 5 ³ cm ³ V = 125 cm ³

Soal 2

Sebuah balok memiliki panjang 10 cm, lebar 8 cm, dan tinggi 5 cm. Berapakah volume balok tersebut?

Pembahasan

Rumus volume balok: V = p × l × tDiketahui: p = 10 cm, l = 8 cm, t = 5 cmV = 10 cm × 8 cm × 5 cmV = 400 cm ³

Soal 3

Hitunglah volume kerucut yang memiliki jari-jari alas 7 cm dan tinggi 24 cm.

Pembahasan

Rumus volume kerucut: V = 1/3 × π × r ² × tDiketahui: r = 7 cm, t = 24 cmV = 1/3 × π × 7 ² cm ² × 24 cmV = 396π cm ³ ≈ 1242,75 cm ³

Soal 4

Sebuah tabung memiliki jari-jari alas 10 cm dan tinggi 15 cm. Tentukan volume tabung tersebut.

Pembahasan

Rumus volume tabung: V = π × r ² × tDiketahui: r = 10 cm, t = 15 cmV = π × 10 ² cm ² × 15 cmV = 1500π cm ³ ≈ 4712,39 cm ³

Soal 5

Hitunglah volume bola yang memiliki jari-jari 14 cm.

Pembahasan

Rumus volume bola: V = 4/3 × π × r ³ Diketahui: r = 14 cmV = 4/3 × π × 14 ³ cm ³ V = 11304π cm ³ ≈ 35342,79 cm ³

Aplikasi Bangun Ruang dalam Kehidupan

Bangun ruang memiliki peran penting dalam berbagai aspek kehidupan, dari arsitektur hingga teknik dan banyak lagi. Pemahaman tentang bangun ruang dan sifat-sifatnya sangat penting untuk merancang dan membangun struktur yang kokoh, fungsional, dan estetis.

Arsitektur

Dalam arsitektur, bangun ruang digunakan untuk menciptakan ruang dan bentuk bangunan. Bangun ruang dasar seperti kubus, balok, dan prisma digunakan sebagai dasar untuk desain arsitektur, sementara bentuk yang lebih kompleks seperti silinder, kerucut, dan bola dapat digunakan untuk menciptakan fitur arsitektur yang unik dan menarik.

• Kubus dan Balok: Digunakan untuk membuat ruang persegi panjang dan kamar.
• Prisma: Digunakan untuk membuat ruang berbentuk prisma, seperti atap rumah.
• Silinder: Digunakan untuk membuat menara dan kolom.
• Kerucut: Digunakan untuk membuat atap dan kubah.
• Bola: Digunakan untuk membuat kubah dan menara observasi.

Teknik

Dalam teknik, bangun ruang digunakan untuk menganalisis kekuatan dan stabilitas struktur. Insinyur menggunakan prinsip-prinsip geometri untuk menghitung tegangan dan regangan pada struktur, seperti jembatan, bangunan, dan mesin.

• Balok: Digunakan untuk menganalisis kekuatan dan stabilitas jembatan.
• Silinder: Digunakan untuk menganalisis kekuatan dan stabilitas pipa dan tangki.
• Kerucut: Digunakan untuk menganalisis kekuatan dan stabilitas roket dan kerang.
• Bola: Digunakan untuk menganalisis kekuatan dan stabilitas kapal selam dan bola tangki.

Aplikasi Lainnya

Selain arsitektur dan teknik, bangun ruang juga memiliki banyak aplikasi dalam kehidupan sehari-hari. Misalnya:

• Kubus: Digunakan sebagai kemasan untuk berbagai produk.
• Balok: Digunakan sebagai balok bangunan.
• Prisma: Digunakan sebagai atap tenda dan struktur sementara.
• Silinder: Digunakan sebagai kaleng, pipa, dan wadah lainnya.
• Kerucut: Digunakan sebagai kerucut lalu lintas dan corong.
• Bola: Digunakan sebagai bola olahraga dan lampu hias.

Penutupan

Dengan memahami nama-nama dan gambar bangun ruang, kita dapat mengembangkan pemahaman yang lebih mendalam tentang dunia tiga dimensi. Pengetahuan ini tidak hanya memperkaya pengetahuan kita, tetapi juga membekali kita dengan alat yang berharga untuk memecahkan masalah dan membuat keputusan yang tepat dalam berbagai bidang kehidupan.

Tanya Jawab (Q&A)

Apa saja jenis-jenis bangun ruang yang paling umum?

Kubus, balok, prisma, limas, kerucut, silinder, dan bola.

Bagaimana cara menghitung volume bangun ruang?

Tergantung pada jenis bangun ruangnya. Setiap jenis memiliki rumus volume yang unik.

Apa aplikasi bangun ruang dalam kehidupan sehari-hari?

Bangun ruang digunakan dalam arsitektur, teknik, desain produk, dan banyak lagi.