Dunia trigonometri dipenuhi dengan identitas dan hubungan yang menakjubkan, dan di antara yang paling mendasar adalah sin(a + b) = sin(a)cos(b) + cos(a)sin(b). Identitas ini membuka jalan untuk penyederhanaan ekspresi trigonometri yang kompleks.
Dalam eksplorasi ini, kita akan menyelami nilai khusus dari sin 15 dan sin 75 derajat, mengungkap hubungan yang menarik di antara keduanya. Perjalanan kita akan membawa kita melalui identitas setengah sudut, hubungan pelengkap, dan aplikasi praktis dari nilai-nilai ini dalam berbagai bidang.
Identitas Trigonometri

Identitas trigonometri adalah persamaan yang melibatkan fungsi trigonometri (seperti sinus, kosinus, tangen, kotangen, sekan, dan kosekan) yang selalu benar untuk setiap nilai sudut.
Salah satu identitas trigonometri yang umum digunakan adalah sin(a + b) = sin(a)cos(b) + cos(a)sin(b).
Contoh Penggunaan Identitas Trigonometri
Identitas ini dapat digunakan untuk menyederhanakan ekspresi trigonometri. Misalnya, kita dapat menggunakan identitas ini untuk menyederhanakan ekspresi sin(45°)cos(30°) + cos(45°)sin(30°) sebagai berikut:
sin(45°)cos(30°) + cos(45°)sin(30°) = (√2/2)(√3/2) + (√2/2)(1/2) = √6/4 + √2/4 = (√6 + √2)/4
Nilai Sin 15 Derajat
Untuk menghitung nilai sin 15 derajat, kita dapat menggunakan identitas setengah sudut:
sin(30/2) = √((1 – cos 30)/2)
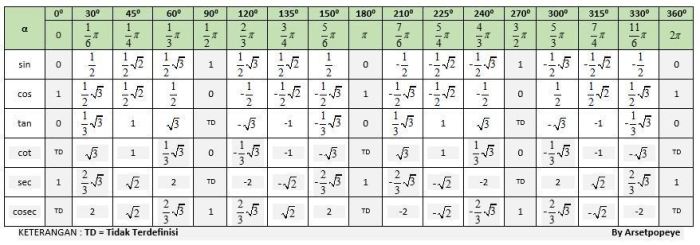
Kita dapat menggunakan tabel berikut untuk menghitung nilai cos 30 dan sin 30:
| Sudut | cos | sin |
|---|---|---|
| 0° | 1 | 0 |
| 30° | √3/2 | 1/2 |
| 60° | 1/2 | √3/2 |
| 90° | 0 | 1 |
Dengan menggunakan tabel tersebut, kita dapat menghitung sin 15 derajat sebagai berikut:
sin 15 derajat = sin (30/2) = √((1 – √3/2)/2) = √((2 – √3)/4) = √(1 – √3/4)
Nilai Sin 75 Derajat
Sinus dari 75 derajat dapat dihitung menggunakan identitas trigonometri sin(90 – a) = cos a.
Identitas Trigonometri
- sin(90
– a) = cos a
Menggunakan identitas ini, kita dapat menghitung sin 75 derajat sebagai berikut:
sin 75° = cos (90°
75°) = cos 15°
Dengan demikian, sin 75 derajat sama dengan cos 15 derajat.
Hubungan antara Sin 75 dan Sin 15
Dari identitas sin(90 – a) = cos a, kita dapat menyimpulkan bahwa:
sin 75° = cos 15°sin 15° = cos 75°
Oleh karena itu, sin 75 derajat dan sin 15 derajat saling melengkapi.
Aplikasi Nilai Sin 15 dan 75 Derajat

Nilai sinus 15° dan 75° memiliki aplikasi luas dalam berbagai bidang, termasuk teknik, navigasi, dan fisika. Nilai-nilai ini digunakan untuk menghitung jarak, sudut, dan besaran fisika lainnya.
Teknik
- Desain Arsitektur: Sin 15° digunakan untuk menghitung ketinggian bangunan atau objek lain dari jarak yang diketahui.
- Teknik Sipil: Sin 75° digunakan untuk menghitung sudut kemiringan jalan atau jembatan.
Navigasi
- Penentuan Posisi: Sin 15° digunakan untuk menghitung jarak dari kapal ke garis pantai yang terlihat dari ketinggian tertentu.
- Penentuan Arah: Sin 75° digunakan untuk menghitung sudut antara arah utara dan arah yang ditempuh kapal.
Fisika
- Getaran Harmonik: Sin 15° dan 75° digunakan untuk menghitung amplitudo dan periode getaran harmonik.
- Gelombang: Sin 75° digunakan untuk menghitung panjang gelombang dan frekuensi gelombang.
Kesimpulan

Setelah meneliti nilai sin 15 dan sin 75, kita sampai pada kesimpulan bahwa identitas trigonometri menyediakan alat yang ampuh untuk menyederhanakan ekspresi dan mengungkap hubungan yang tersembunyi. Nilai-nilai ini tidak hanya penting secara teoritis, tetapi juga memiliki aplikasi luas dalam bidang teknik, navigasi, dan fisika.
Dengan memahami nilai-nilai ini, kita membuka kunci pemahaman yang lebih dalam tentang dunia trigonometri dan penggunaannya yang beragam.
Jawaban untuk Pertanyaan Umum
Mengapa nilai sin 15 dan sin 75 penting?
Nilai-nilai ini sering muncul dalam aplikasi praktis, seperti menghitung sudut dalam segitiga atau menyelesaikan persamaan trigonometri.
Bagaimana cara menghitung sin 15 derajat?
Menggunakan identitas setengah sudut, sin(15) = √((1 – cos 30)/2).
Apakah sin 75 dan cos 15 terkait?
Ya, sin 75 = cos 15, karena keduanya adalah sudut komplementer (jumlahnya 90 derajat).