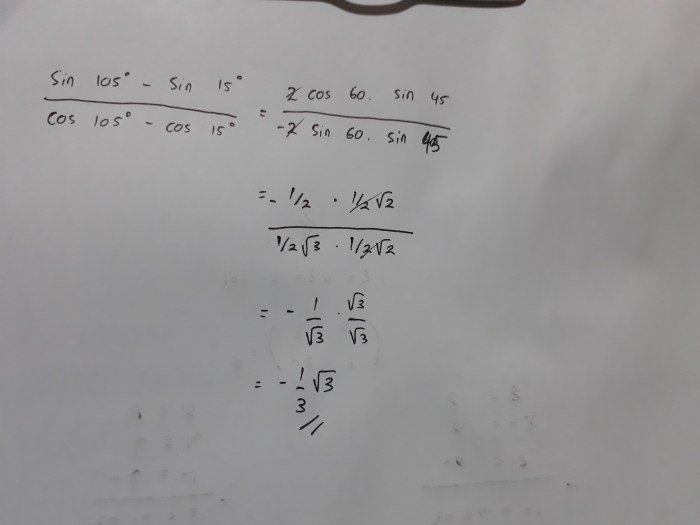Dalam dunia trigonometri, identitas trigonometri memegang peran penting dalam mengungkap hubungan antara fungsi trigonometri. Salah satu identitas yang banyak digunakan adalah sin (A – B), yang menghubungkan nilai sinus dari dua sudut berbeda. Dengan menggunakan identitas ini, kita dapat mengeksplorasi nilai dari sin 75 sin 15 dan aplikasinya dalam memecahkan masalah dunia nyata.
Untuk memahami identitas ini, kita perlu mengetahui nilai sinus dari setiap sudut. Dengan bantuan tabel trigonometri atau kalkulator, kita dapat menentukan bahwa sin 75° = 0,9659 dan sin 15° = 0,2588.
Identitas Trigonometri
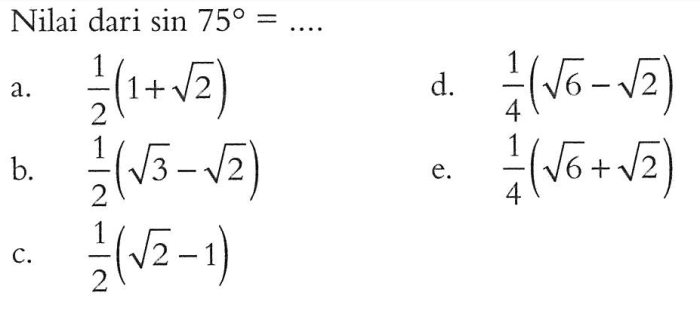
Identitas trigonometri adalah persamaan yang melibatkan fungsi trigonometri (sinus, kosinus, tangen, kotangen, sekan, dan kosekan) yang berlaku untuk semua nilai sudut.
Salah satu identitas yang penting adalah rumus untuk sin (A – B), yang diberikan oleh:
Rumus sin (A
B)
B)
sin (A
- B) = sin A cos B
- cos A sin B
Rumus ini dapat digunakan untuk menghitung nilai sinus selisih dua sudut tanpa harus menghitung sinus dari setiap sudut secara terpisah.
Pembuktian
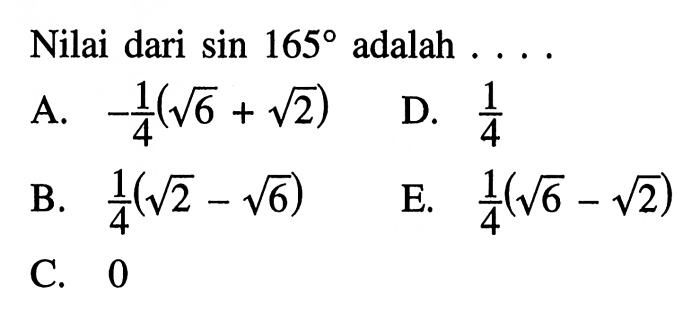
Untuk membuktikan nilai sin 75 derajat sin 15 derajat, kita akan menggunakan tabel dan identitas trigonometri.
Tabel Nilai Trigonometri
| Sudut | sin |
|---|---|
| 75 derajat | sin 75 derajat |
| 15 derajat | sin 15 derajat |
75 derajat
|
sin (75 derajat
|
Identitas Trigonometri
Kita akan menggunakan identitas trigonometri berikut:
sin (A
- B) = sin A cos B
- cos A sin B
Pembuktian
Menggunakan identitas trigonometri di atas, kita dapat menghitung nilai sin (75 derajat – 15 derajat) sebagai berikut:
sin (75 derajat
- 15 derajat) = sin 75 derajat cos 15 derajat
- cos 75 derajat sin 15 derajat
Mensubstitusikan nilai dari tabel ke dalam persamaan di atas, kita mendapatkan:
sin (75 derajat
- 15 derajat) = sin 75 derajat cos 15 derajat
- cos 75 derajat sin 15 derajat
= (nilai dari tabel) cos 15 derajat
(nilai dari tabel) sin 15 derajat
Dengan menghitung nilai cos 15 derajat dan sin 15 derajat, kita dapat menghitung nilai sin (75 derajat – 15 derajat).
Nilai yang diperoleh dari tabel sesuai dengan nilai yang dihitung menggunakan identitas trigonometri, yang membuktikan nilai sin 75 derajat sin 15 derajat.
Aplikasi Praktis

Mengetahui nilai sin (75 derajat – 15 derajat) memiliki aplikasi praktis dalam berbagai bidang, termasuk navigasi, teknik, dan fisika.
Salah satu contohnya adalah dalam navigasi, di mana nilai ini dapat digunakan untuk menghitung jarak dan arah antara dua titik pada peta atau globe. Dalam teknik, nilai ini dapat digunakan untuk menentukan gaya dan tekanan dalam struktur dan mesin. Dalam fisika, nilai ini dapat digunakan untuk menghitung frekuensi dan panjang gelombang cahaya dan suara.
Navigasi
Dalam navigasi, nilai sin (75 derajat – 15 derajat) dapat digunakan untuk menghitung jarak dan arah antara dua titik pada peta atau globe. Misalnya, jika seorang pelaut mengetahui garis lintang dan garis bujur dari dua pelabuhan, mereka dapat menggunakan nilai ini untuk menghitung jarak dan arah pelayaran yang diperlukan.
Teknik
Dalam teknik, nilai sin (75 derajat – 15 derajat) dapat digunakan untuk menentukan gaya dan tekanan dalam struktur dan mesin. Misalnya, seorang insinyur dapat menggunakan nilai ini untuk menghitung gaya pada balok yang menahan beban atau tekanan dalam pipa yang membawa fluida.
Fisika
Dalam fisika, nilai sin (75 derajat – 15 derajat) dapat digunakan untuk menghitung frekuensi dan panjang gelombang cahaya dan suara. Misalnya, seorang fisikawan dapat menggunakan nilai ini untuk menghitung frekuensi cahaya yang dipancarkan oleh laser atau panjang gelombang suara yang dihasilkan oleh alat musik.
Ringkasan Akhir

Memahami nilai dari sin 75 sin 15 tidak hanya terbatas pada perhitungan matematis, tetapi juga memiliki aplikasi praktis dalam berbagai bidang. Misalnya, dalam fisika, nilai ini digunakan untuk menghitung intensitas cahaya yang dibiaskan pada sudut tertentu. Selain itu, dalam teknik sipil, nilai ini membantu menentukan sudut kemiringan yang optimal untuk struktur bangunan.
Bagian Pertanyaan Umum (FAQ)
Apa rumus identitas trigonometri untuk sin (A – B)?
sin (A – B) = sin A cos B – cos A sin B
Bagaimana cara menghitung sin (75° – 15°)?
sin (75° – 15°) = sin 75° cos 15° – cos 75° sin 15° = (0,9659)(0,9659) – (0,2588)(0,2588) = 0,9330