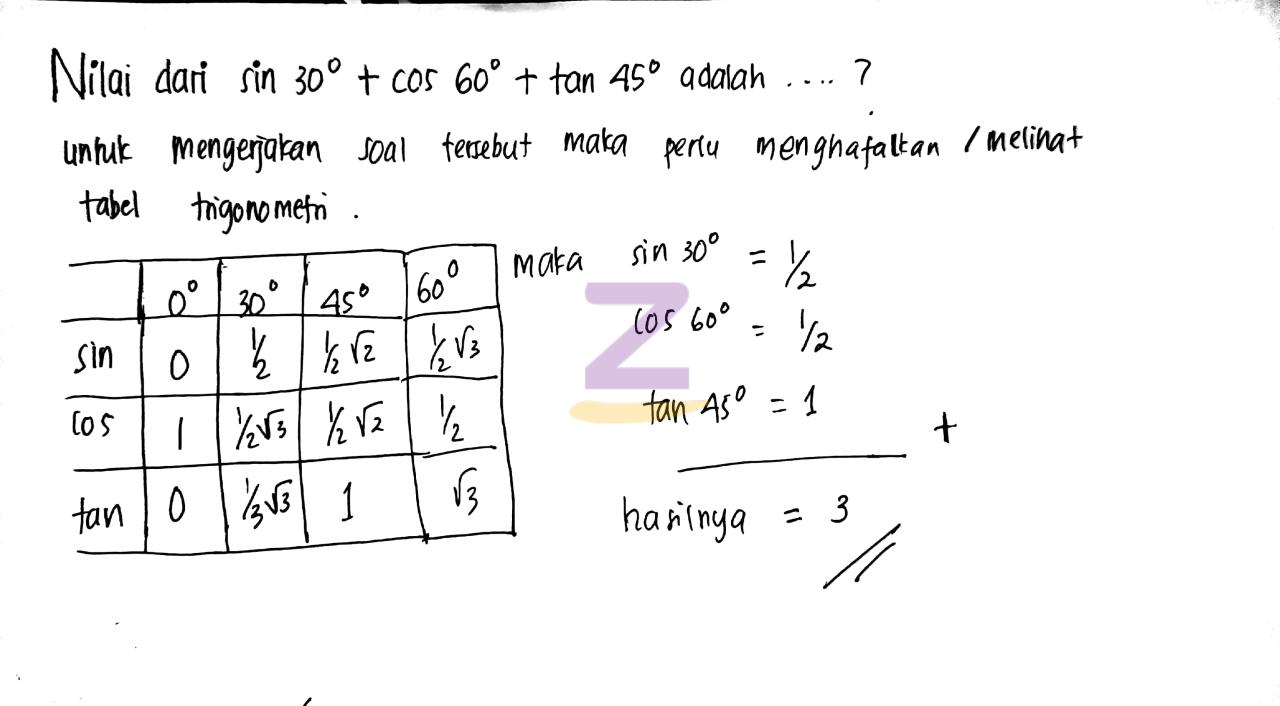
Dalam dunia trigonometri, terdapat hubungan menarik antara nilai sinus dan kosinus pada sudut-sudut tertentu. Salah satu hubungan yang menonjol adalah keterkaitan antara nilai sin 45°, cos 15°, cos 45°, dan sin 15°. Hubungan ini tidak hanya memiliki signifikansi matematis, tetapi juga memiliki aplikasi praktis dalam berbagai bidang.

Hubungan antara nilai-nilai trigonometri ini akan dibahas secara mendalam dalam uraian berikut, memberikan pemahaman yang komprehensif tentang sifat dan penerapannya.

Rumus Trigonometri

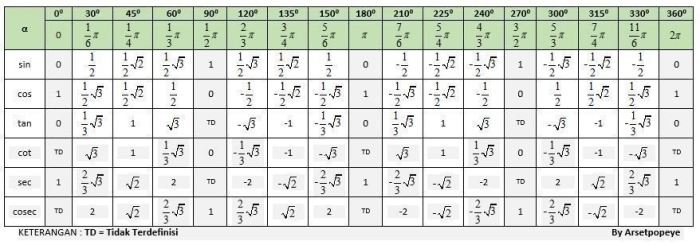
Rumus trigonometri adalah rumus matematika yang digunakan untuk menghitung sisi dan sudut segitiga siku-siku. Rumus-rumus ini didasarkan pada hubungan antara sisi dan sudut segitiga, dan dapat digunakan untuk menyelesaikan berbagai masalah.

Rumus Sinus

Rumus sinus menyatakan bahwa perbandingan panjang sisi yang berlawanan dengan sudut tertentu dengan panjang sisi miring adalah sama dengan sinus sudut tersebut. Secara matematis, rumus sinus dapat ditulis sebagai:

sin(A) = sin(B) = sin(C) = a/c = b/c = c/a

di mana A, B, dan C adalah sudut-sudut segitiga, a, b, dan c adalah panjang sisi-sisinya, dan c adalah panjang sisi miring.

Rumus Kosinus

Rumus kosinus menyatakan bahwa kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang kedua sisi lainnya dikurangi dua kali hasil kali panjang kedua sisi tersebut dengan kosinus sudut di antara keduanya. Secara matematis, rumus kosinus dapat ditulis sebagai:

c^2 = a^2 + b^2

2abcos(C)

di mana a dan b adalah panjang sisi-sisinya, c adalah panjang sisi miring, dan C adalah sudut di antara sisi a dan b.

Nilai Sinus dan Kosinus

Dalam trigonometri, sinus dan kosinus adalah fungsi trigonometri yang sangat penting. Nilai-nilai fungsi ini untuk sudut-sudut umum sering digunakan dalam perhitungan dan aplikasi trigonometri.

Tabel Nilai Sinus dan Kosinus

Berikut adalah tabel nilai sinus dan kosinus untuk sudut-sudut umum:

Sudut	Sinus	Kosinus
0°	0	1
15°	0,2588	0,9659
30°	0,5	0,8660
45°	0,7071	0,7071
60°	0,8660	0,5
75°	0,9659	0,2588
90°	1	0

Pola Nilai Sinus dan Kosinus

Dari tabel di atas, dapat diamati beberapa pola berikut:

• Nilai sinus dan kosinus berlawanan untuk sudut yang saling melengkapi (misalnya, 30° dan 60°).
• Nilai sinus dan kosinus sama untuk sudut yang sama besar (misalnya, 45° dan 45°).
• Nilai sinus dan kosinus simetris terhadap garis 45°. Artinya, nilai sinus sudut θ sama dengan nilai kosinus sudut (90°
  – θ).

Identitas Trigonometri

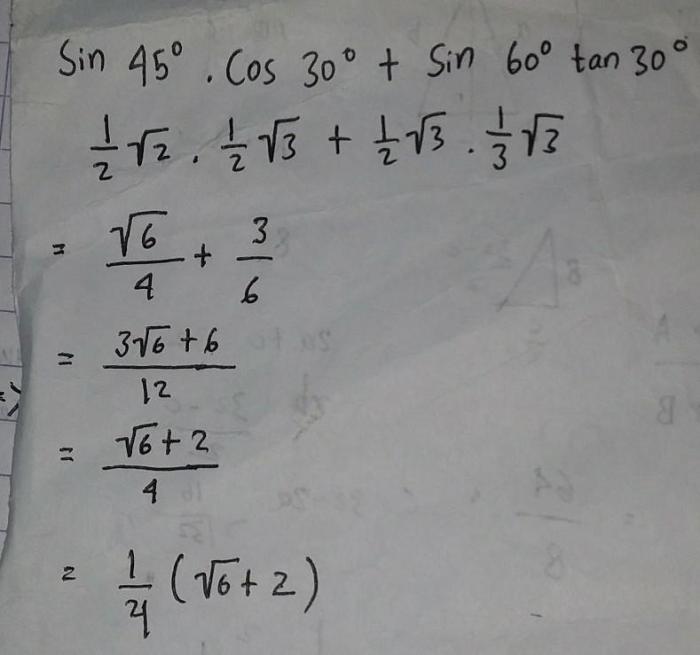
Identitas trigonometri adalah persamaan yang melibatkan fungsi trigonometri seperti sinus, kosinus, dan tangen. Identitas ini sangat penting dalam trigonometri karena memungkinkan kita untuk menyederhanakan ekspresi trigonometri dan menyelesaikan persamaan trigonometri.

Identitas Sinus dan Kosinus

• sin(A + B) = sin A cos B + cos A sin B
• sin(A
  – B) = sin A cos B
  – cos A sin B
• cos(A + B) = cos A cos B
  – sin A sin B
• cos(A
  – B) = cos A cos B + sin A sin B

Identitas ini dapat digunakan untuk menyederhanakan ekspresi trigonometri dengan mengubah penjumlahan atau pengurangan sudut menjadi perkalian fungsi trigonometri. Misalnya, kita dapat menggunakan identitas ini untuk mengubah sin(45° + 15°) menjadi sin 45° cos 15° + cos 45° sin 15°, yang lebih mudah dievaluasi.

Aplikasi dalam Geometri

Nilai sinus dan kosinus memiliki peran penting dalam menyelesaikan masalah geometri. Nilai-nilai ini memungkinkan kita menentukan panjang sisi, tinggi, dan sudut segitiga.

Mencari Tinggi Segitiga

Untuk mencari tinggi segitiga siku-siku, kita menggunakan rumus:

tinggi = sisi depan / sinus sudut yang berlawanan

Contohnya, jika kita memiliki segitiga siku-siku dengan sisi depan 10 cm dan sudut yang berlawanan dengan tinggi 30 derajat, maka tinggi segitiga tersebut adalah:

tinggi = 10 cm / sin 30°tinggi ≈ 5,77 cm

Mencari Panjang Sisi Miring

Untuk mencari panjang sisi miring segitiga siku-siku, kita menggunakan rumus:

sisi miring = sisi depan / kosinus sudut yang berdekatan

Contohnya, jika kita memiliki segitiga siku-siku dengan sisi depan 8 cm dan sudut yang berdekatan dengan sisi miring 45 derajat, maka panjang sisi miring tersebut adalah:

sisi miring = 8 cm / cos 45°sisi miring ≈ 11,31 cm

Simpulan Akhir

Dengan demikian, hubungan antara nilai sin 45°, cos 15°, cos 45°, dan sin 15° tidak hanya menyoroti keindahan matematika, tetapi juga memberikan alat yang berharga untuk memecahkan masalah dalam geometri dan aplikasi praktis. Memahami hubungan ini sangat penting untuk menguasai trigonometri dan menghargai kekuatannya sebagai alat untuk eksplorasi matematis dan pemecahan masalah.

Bagian Pertanyaan Umum (FAQ)

Apa hubungan antara sin 45° dan cos 45°?

Sin 45° = Cos 45° = √2/2

Bagaimana cara membuktikan sin 15° = (√6 – √2)/4?

Menggunakan identitas setengah sudut dan rumus penjumlahan sudut

Apa saja aplikasi praktis dari hubungan ini?

Menyelesaikan masalah geometri, menentukan tinggi dan panjang sisi miring segitiga, dan dalam navigasi