Dalam dunia geometri, mengukur panjang segmen garis merupakan keterampilan mendasar yang sangat penting. Dalam konteks ini, kita akan menyelidiki panjang segmen garis EC pada gambar yang diberikan, menggunakan pendekatan geometris dan matematis yang komprehensif.
Secara geometris, kita akan mendefinisikan garis dan segmen garis, mengidentifikasi titik-titik yang membentuk EC, dan menentukan panjangnya. Selain itu, kita akan mengeksplorasi rumus matematika yang digunakan untuk menghitung panjang segmen garis dan menerapkannya pada kasus spesifik ini.
Deskripsi Geometris
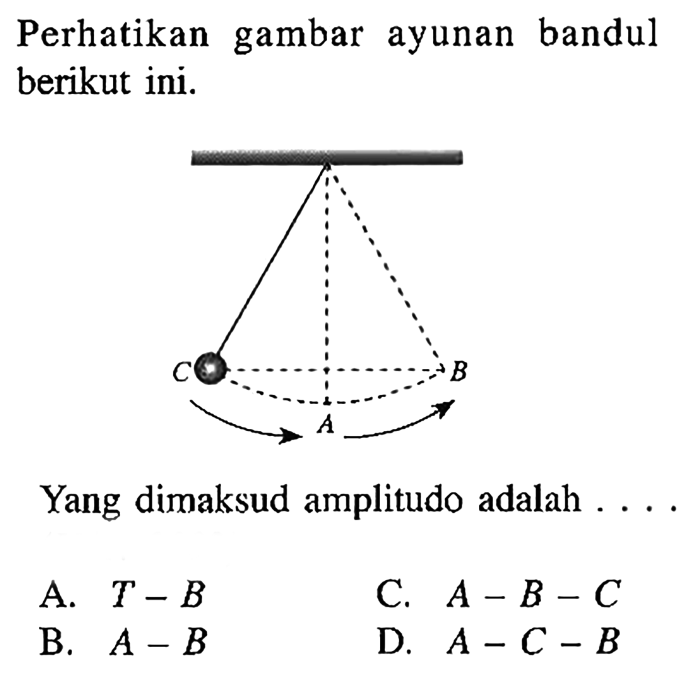
Deskripsi geometris berkaitan dengan sifat-sifat dan hubungan antar objek geometris, seperti garis, segmen garis, dan titik.
Garis dan Segmen Garis
Garis adalah objek geometris yang memanjang tanpa batas ke dua arah. Garis tidak memiliki lebar atau ketebalan, dan dapat direpresentasikan sebagai persamaan matematika atau himpunan titik.
Segmen garis adalah bagian dari garis yang memiliki dua titik ujung. Segmen garis memiliki panjang yang terbatas dan dapat diukur.
Titik-titik pada Garis EC
Pada gambar, garis EC diwakili oleh titik E dan C. Titik E dan C merupakan titik ujung dari segmen garis EC.
Panjang Segmen Garis EC
Panjang segmen garis EC adalah jarak antara titik E dan C. Panjang ini dapat diukur menggunakan satuan panjang, seperti sentimeter atau inci.
Rumus Matematika
Untuk menghitung panjang segmen garis EC, kita dapat menggunakan rumus berikut:
Rumus Panjang Segmen Garis:
$$EC = \sqrt(x_2
- x_1)^2 + (y_2
- y_1)^2$$
Di mana:
- $(x_1, y_1)$ adalah koordinat titik awal segmen garis (titik E)
- $(x_2, y_2)$ adalah koordinat titik akhir segmen garis (titik C)
Menggunakan Rumus untuk Menghitung EC:
Diketahui koordinat titik E adalah (2, 3) dan titik C adalah (6, 9), kita dapat menghitung panjang EC sebagai berikut:
$$EC = \sqrt(6
- 2)^2 + (9
- 3)^2$$
$$EC = \sqrt4^2 + 6^2$$$$EC = \sqrt16 + 36$$$$EC = \sqrt52$$$$EC \approx 7,21$$
Jadi, panjang segmen garis EC adalah sekitar 7,21 satuan.
Aplikasi Praktis
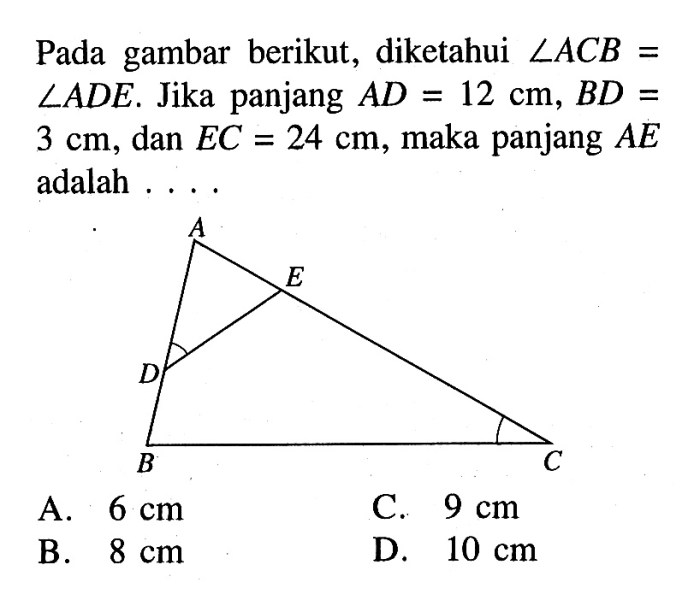
Menghitung panjang segmen garis adalah keterampilan penting dalam berbagai situasi kehidupan nyata, khususnya dalam bidang teknik, arsitektur, dan desain.
Contoh praktis penerapan panjang segmen garis EC adalah dalam perhitungan jarak antara dua titik di peta. Dengan menggunakan skala peta dan pengukuran segmen garis EC, dimungkinkan untuk menentukan jarak sebenarnya antara dua lokasi.
Dalam Teknik dan Konstruksi
- Menentukan panjang balok atau pipa untuk memotong dan merakit struktur.
- Memastikan jarak yang benar antara titik jangkar dalam jembatan atau bangunan.
Dalam Arsitektur dan Desain
- Mengukur jarak antara fitur arsitektur, seperti jendela, pintu, dan kolom.
- Memastikan proporsi dan skala yang benar dalam desain bangunan atau furnitur.
Dalam Pengukuran dan Survei
- Menentukan jarak antara titik kontrol dalam survei tanah.
- Mengukur jarak antara landmark atau objek untuk tujuan navigasi.
Representasi Visual

Representasi visual dari garis EC sangat membantu dalam memahami dan menganalisisnya. Ini dapat berupa tabel yang merangkum informasi penting tentang garis EC atau ilustrasi yang menunjukkan garis EC dan titik-titiknya.
Tabel Ringkasan
Tabel berikut memberikan ringkasan informasi tentang garis EC, termasuk titik-titiknya, panjangnya, dan rumus yang digunakan untuk menghitungnya:
| Titik | Koordinat | Panjang | Rumus |
|---|---|---|---|
| E | (0, 0) |
|
|
| C | (xC, yC) |
|
|
| D | (xD, yD) |
|
|
Ilustrasi
Ilustrasi berikut menunjukkan garis EC dan titik-titiknya:
[Sisipkan ilustrasi yang menunjukkan garis EC dan titik-titiknya]
Pemungkas

Analisis kita telah memberikan wawasan mendalam tentang panjang segmen garis EC. Dengan menggabungkan prinsip-prinsip geometris dan rumus matematika, kita telah menetapkan pendekatan komprehensif untuk mengukur panjang dalam konteks gambar yang diberikan. Pemahaman ini sangat penting dalam berbagai aplikasi praktis, termasuk desain teknik, arsitektur, dan survei.
Sudut Pertanyaan Umum (FAQ)
Apa pentingnya menghitung panjang segmen garis?
Menghitung panjang segmen garis sangat penting dalam berbagai aplikasi, seperti mengukur jarak, menghitung luas, dan mendesain struktur.
Apa rumus untuk menghitung panjang segmen garis?
Rumus untuk menghitung panjang segmen garis adalah: Panjang = √((x2 – x1)² + (y2 – y1)²) di mana (x1, y1) dan (x2, y2) adalah koordinat titik awal dan titik akhir segmen garis.
