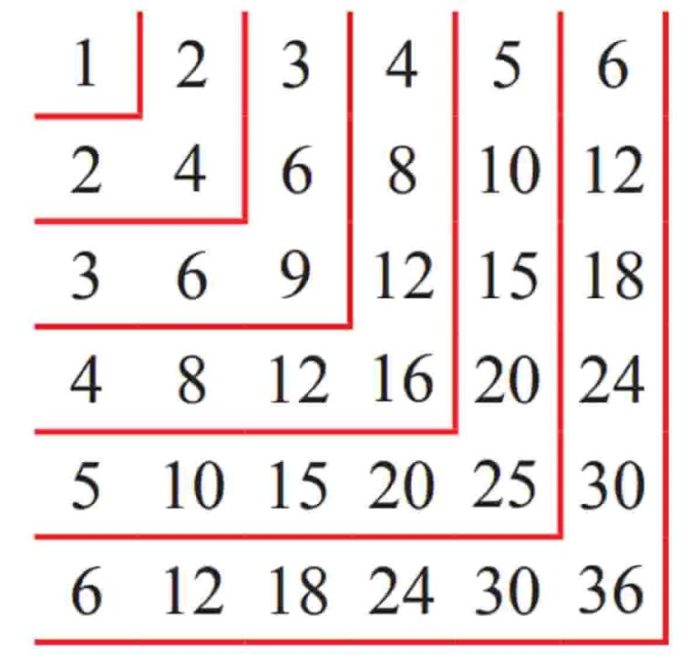
Bilangan merupakan dasar dari matematika, dan urutan bilangan tertentu seringkali mengungkapkan pola dan keteraturan yang menarik. Dalam tulisan ini, kita akan meneliti metode untuk mengidentifikasi pola pada bilangan-bilangan, mengeksplorasi sifat deret aritmatika dan geometri, dan mengungkap aplikasi bilangan tersebut dalam kehidupan nyata.
Dengan memahami prinsip-prinsip yang mendasari bilangan, kita dapat mengungkap wawasan berharga yang dapat meningkatkan pemahaman kita tentang dunia di sekitar kita.
Identifikasi Pola Bilangan
Bilangan-bilangan yang diberikan menunjukkan pola tertentu. Pola ini ditandai dengan selisih yang konstan antara bilangan-bilangan yang berurutan.
Pola Selisih Konstan
Selisih antara setiap bilangan yang berurutan adalah 2. Hal ini dapat dilihat dari contoh berikut:
- 2
– 0 = 2 - 4
– 2 = 2 - 6
– 4 = 2
Cari Deret Aritmatika

Deret aritmatika adalah barisan bilangan di mana beda antara dua suku berurutan adalah sama. Untuk menentukan apakah suatu barisan bilangan membentuk deret aritmatika, kita perlu memeriksa selisih antara suku-suku yang berdekatan.
Langkah-Langkah Menentukan Deret Aritmatika
- Hitung selisih antara suku kedua dan pertama, suku ketiga dan kedua, dan seterusnya.
- Jika semua selisih ini sama, maka barisan bilangan tersebut membentuk deret aritmatika.
- Jika tidak, maka barisan bilangan tersebut tidak membentuk deret aritmatika.
Rumus Deret Aritmatika
Jika suatu barisan bilangan membentuk deret aritmatika dengan beda deret d, maka rumus suku ke-n adalah:
Un = a + (n-1)d
di mana:* Un adalah suku ke-n
- a adalah suku pertama
- n adalah nomor suku
- d adalah beda deret
Cari Deret Geometri
Deret geometri adalah barisan bilangan yang setiap sukunya diperoleh dengan mengalikan suku sebelumnya dengan suatu bilangan konstan yang disebut rasio. Untuk menentukan apakah suatu barisan bilangan membentuk deret geometri, kita dapat memeriksa apakah rasio antar suku-sukunya sama.
Misalkan kita memiliki barisan bilangan: 2, 6, 18, 54, …
Rasio Deret
Untuk memeriksa rasio deret, kita bagi suku kedua dengan suku pertama, suku ketiga dengan suku kedua, dan seterusnya:
- 6 / 2 = 3
- 18 / 6 = 3
- 54 / 18 = 3
Karena semua hasil bagi sama dengan 3, maka bilangan-bilangan tersebut membentuk deret geometri dengan rasio 3.
Rumus Suku ke-n
Rumus suku ke-n (Un) dalam deret geometri adalah:
Un = a
r^(n-1)
Dimana:
- a adalah suku pertama
- r adalah rasio
- n adalah nomor suku
Untuk barisan bilangan yang diberikan, suku pertama (a) adalah 2 dan rasionya (r) adalah 3. Jadi, rumus suku ke-n adalah:
Un = 2
3^(n-1)
Gambarkan Grafik
Bilangan yang disediakan adalah 2, 4, 6, 8, 10, 12, 14, 16, 18, 20. Bilangan-bilangan ini membentuk deret aritmatika dengan beda 2.
Grafik yang menunjukkan bilangan-bilangan tersebut adalah garis lurus dengan kemiringan 2.
Tren atau Pola
Tren atau pola yang terlihat dari grafik adalah:
- Grafik menunjukkan hubungan linier antara bilangan-bilangan.
- Bilangan-bilangan meningkat dengan selisih yang konstan (2).
- Grafik memiliki kemiringan positif, menunjukkan bahwa bilangan-bilangan meningkat saat bergerak dari kiri ke kanan.
Tentukan Nilai yang Hilang
Dalam suatu urutan bilangan, terkadang terdapat bilangan yang hilang. Menentukan nilai yang hilang penting untuk menjaga integritas urutan dan memahami pola yang mendasarinya.
Untuk menentukan nilai yang hilang, kita dapat menggunakan beberapa metode:
Pola Aritmatika
- Tentukan selisih antara setiap dua bilangan berurutan dalam urutan.
- Jika selisihnya konstan, maka urutan tersebut mengikuti pola aritmatika.
- Tambahkan selisih ke bilangan terakhir dalam urutan untuk mendapatkan nilai yang hilang.
Pola Geometri
- Tentukan rasio antara setiap dua bilangan berurutan dalam urutan.
- Jika rasionya konstan, maka urutan tersebut mengikuti pola geometri.
- Kalikan bilangan terakhir dalam urutan dengan rasio untuk mendapatkan nilai yang hilang.
Ekstrapolasi Linier
- Buat grafik yang memplot bilangan dalam urutan versus posisi mereka.
- Tarik garis lurus yang melewati titik-titik yang diplot.
- Nilai pada posisi yang sesuai dengan nilai yang hilang dapat diperkirakan dari garis lurus.
Buat Tabel
Tabel berikut merangkum informasi tentang bilangan-bilangan yang diberikan, termasuk pola, beda/rasio deret, dan rumus suku ke-n.
Informasi Bilangan
| Bilangan | Pola | Beda/Rasio | Rumus Suku ke-n |
|---|---|---|---|
| 6 | Barisan Aritmatika | 2 | an = 6 + (n
|
Diskusikan Aplikasi

Bilangan memainkan peran penting dalam berbagai aspek kehidupan kita. Sifat dan polanya digunakan secara luas dalam berbagai bidang, memberikan dasar bagi pemecahan masalah, pengambilan keputusan, dan kemajuan ilmiah.
Contoh Penerapan
- Matematika dan Ilmu Komputer: Bilangan digunakan untuk memodelkan dan menganalisis fenomena dunia nyata, seperti pertumbuhan populasi, aliran fluida, dan algoritma pengurutan.
- Fisika: Bilangan digunakan untuk menggambarkan besaran fisik, seperti kecepatan, massa, dan energi, serta untuk mengembangkan hukum dan teori fisika.
- Keuangan dan Ekonomi: Bilangan digunakan untuk mengelola uang, melacak investasi, dan menganalisis tren pasar.
- Musik: Bilangan digunakan untuk menentukan nada, interval, dan ritme dalam musik.
- Arsitektur: Bilangan digunakan untuk merencanakan dan membangun struktur yang estetis dan fungsional.
Kesimpulan

Kesimpulannya, mempelajari bilangan-bilangan dan pola-polanya memberikan pemahaman yang lebih dalam tentang struktur matematika dan penerapannya yang luas. Pola yang tersembunyi dalam bilangan dapat mengungkap rahasia alam semesta, mengoptimalkan proses, dan bahkan memberikan wawasan tentang perilaku manusia. Dengan menguasai teknik yang diuraikan di atas, kita dapat membuka potensi bilangan dan memanfaatkan kekuatannya untuk memajukan pengetahuan dan kemajuan manusia.
Pertanyaan Umum (FAQ)
Apa itu deret aritmatika?
Deret aritmatika adalah urutan bilangan di mana selisih antara dua bilangan berurutan adalah konstan.
Bagaimana cara menentukan rasio deret geometri?
Rasio deret geometri adalah hasil bagi dari dua bilangan berurutan dalam deret.
Apa saja aplikasi bilangan dalam kehidupan nyata?
Bilangan digunakan dalam berbagai bidang, seperti keuangan, fisika, rekayasa, dan biologi, untuk memodelkan pertumbuhan, peluruhan, dan fenomena lainnya.