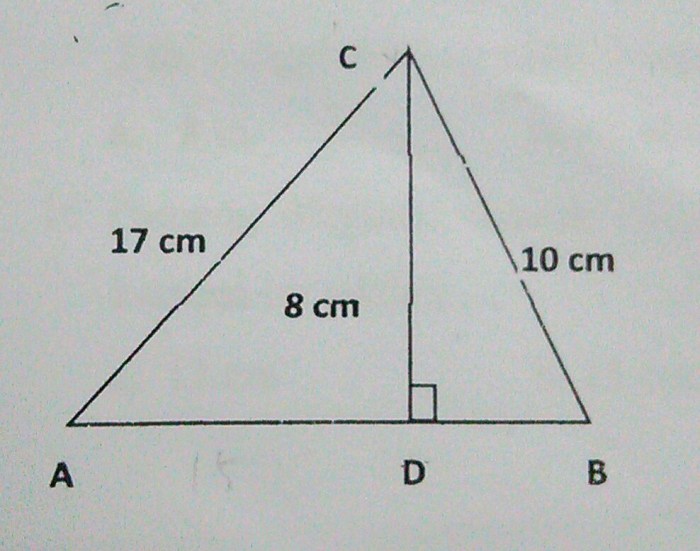
Perhatikan gambar berikut panjang ac adalah – Dalam segitiga siku-siku, menghitung panjang sisi AC merupakan keterampilan penting yang memiliki banyak aplikasi praktis. Artikel ini akan mengulas rumus, teorema, dan penggunaan trigonometri untuk menentukan panjang sisi AC, serta manfaatnya dalam berbagai bidang.

Panjang Sisi AC

Dalam segitiga siku-siku, panjang sisi AC (sisi miring) dapat dihitung menggunakan Teorema Pythagoras, yang menyatakan bahwa kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang sisi lainnya.

Rumus untuk Menghitung Panjang Sisi AC

Rumus Teorema Pythagoras untuk menghitung panjang sisi AC adalah sebagai berikut:

AC² = AB² + BC²

di mana:

• AC adalah panjang sisi miring
• AB dan BC adalah panjang sisi lainnya yang membentuk sudut siku-siku

Contoh Perhitungan

Misalkan kita memiliki segitiga siku-siku dengan panjang sisi AB = 5 cm dan BC = 12 cm. Untuk menghitung panjang sisi AC, kita dapat menggunakan rumus Teorema Pythagoras:

AC² = AB² + BC²AC² = 5² + 12²AC² = 25 + 144AC² = 169AC = √169AC = 13 cm

Dalam mengamati gambar berikut, panjang AC dapat mempengaruhi dampak listrik bagi pelaku industri . Arus listrik yang lebih besar pada AC yang lebih panjang dapat memberikan manfaat seperti peningkatan produktivitas dan efisiensi mesin industri. Hal ini dikarenakan arus listrik yang lebih besar memungkinkan mesin beroperasi pada daya yang lebih tinggi, sehingga mempercepat proses produksi dan meningkatkan output.

Jadi, panjang sisi AC dalam segitiga siku-siku tersebut adalah 13 cm.

Teorema Pythagoras

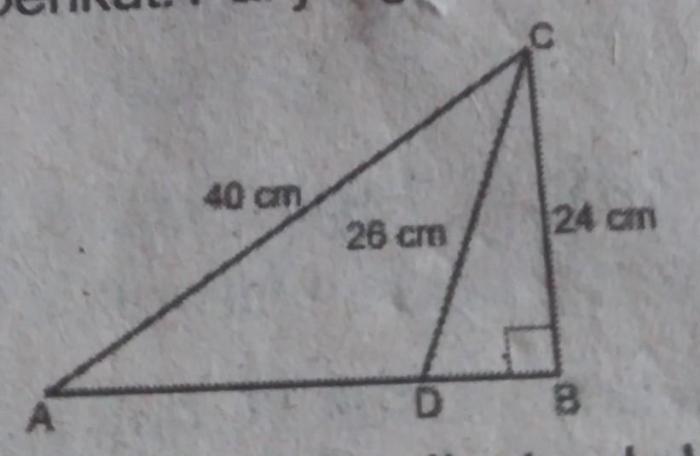
Teorema Pythagoras menyatakan bahwa dalam segitiga siku-siku, kuadrat panjang sisi miring (sisi terpanjang yang berlawanan dengan sudut siku-siku) sama dengan jumlah kuadrat panjang kedua sisi lainnya.

Dalam segitiga siku-siku ABC, di mana AC adalah sisi miring, AB adalah sisi depan, dan BC adalah sisi samping, Teorema Pythagoras dinyatakan sebagai:

AC² = AB² + BC²

Teorema Pythagoras dapat digunakan untuk menghitung panjang sisi miring jika panjang kedua sisi lainnya diketahui. Misalnya, jika AB = 3 cm dan BC = 4 cm, maka AC dapat dihitung sebagai berikut:

AC² = 3² + 4² = 9 + 16 = 25AC = √25 = 5 cm

Aplikasi Teorema Pythagoras, Perhatikan gambar berikut panjang ac adalah

Teorema Pythagoras memiliki berbagai aplikasi dalam bidang seperti:

• Arsitektur dan teknik untuk menghitung panjang balok dan penyangga.
• Navigasi untuk menentukan jarak antara dua titik.
• Trigonometri untuk menghitung nilai fungsi trigonometri.
• Geometri untuk membuktikan sifat-sifat segitiga.

Trigonometri

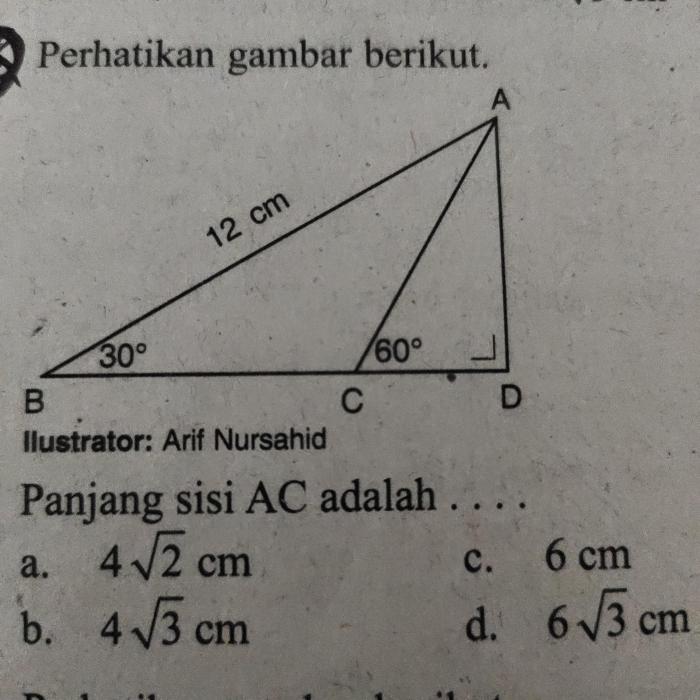
Trigonometri adalah cabang matematika yang mempelajari hubungan antara sisi dan sudut segitiga. Fungsi trigonometri, seperti sinus, kosinus, dan tangen, digunakan untuk menghitung panjang sisi segitiga ketika sisi atau sudut lain diketahui.

Menggunakan Fungsi Trigonometri untuk Menghitung Panjang Sisi AC

Dalam segitiga siku-siku, panjang sisi AC dapat dihitung menggunakan fungsi sinus, kosinus, atau tangen, tergantung pada sisi dan sudut yang diketahui. Rumus yang digunakan adalah:

• Sinus: AC = AB – sin(∠C)
• Kosinus: AC = BC – cos(∠B)
• Tangen: AC = BC – tan(∠B)

Contoh Penggunaan Fungsi Trigonometri

Misalkan kita memiliki segitiga siku-siku dengan AB = 5 cm dan ∠B = 30°. Untuk menghitung panjang sisi AC, kita dapat menggunakan fungsi sinus:

AC = AB – sin(∠C) = 5 cm – sin(30°) = 2,5 cm

Aplikasi Praktis: Perhatikan Gambar Berikut Panjang Ac Adalah

Mengetahui cara menghitung panjang sisi AC memiliki aplikasi luas dalam berbagai bidang, termasuk arsitektur, teknik, dan desain.

Dalam mengamati gambar, panjang AC dapat menjadi acuan penting. Namun, perbedaan waktu antara Indonesia dan negara tetangga juga perlu dipertimbangkan. Misalnya, Singapura memiliki perbedaan waktu beda berapa jam indonesia dengan singapura dengan Indonesia. Pemahaman tentang perbedaan waktu ini dapat membantu dalam mengoordinasikan kegiatan dan komunikasi lintas negara, serta memperhitungkan perbedaan jam kerja dan waktu kedatangan dalam aktivitas yang melibatkan Indonesia dan Singapura.

Arsitektur

Dalam arsitektur, menghitung panjang sisi AC sangat penting untuk menentukan ukuran dan proporsi bangunan. Misalnya, dalam desain rumah, panjang sisi AC digunakan untuk menentukan luas lantai, ketinggian langit-langit, dan ukuran jendela dan pintu.

Teknik

Dalam teknik, menghitung panjang sisi AC penting untuk menganalisis struktur dan stabilitas. Misalnya, dalam desain jembatan, panjang sisi AC digunakan untuk menghitung tegangan dan tekanan pada rangka jembatan, memastikan strukturnya aman dan tahan lama.

Desain

Dalam desain, menghitung panjang sisi AC digunakan untuk menciptakan proporsi yang harmonis dan estetis. Misalnya, dalam desain furnitur, panjang sisi AC digunakan untuk menentukan ukuran dan bentuk kursi, meja, dan lemari, memastikan tampilannya seimbang dan menarik.

Perhatikan gambar berikut panjang AC adalah batas bawah, sementara batas atas ditentukan oleh batas batas keterbukaan ideologi Pancasila . Artinya, segala ideologi yang berada di luar batas tersebut dianggap bertentangan dengan nilai-nilai luhur Pancasila dan tidak dapat dianut di Indonesia.

Namun, dalam konteks penerapannya, terdapat pula batas batas keterbukaan yang lebih fleksibel yang memungkinkan adanya penyesuaian ideologi sesuai dengan perkembangan zaman dan kebutuhan masyarakat.

Manfaat Mengetahui Cara Menghitung Panjang Sisi AC

• Memungkinkan perencanaan dan desain yang akurat dalam berbagai bidang.
• Membantu memastikan keamanan dan stabilitas struktur.
• Meningkatkan estetika dan harmoni dalam desain.
• Menyederhanakan komunikasi dan pemahaman antara profesional dalam bidang yang berbeda.

Ringkasan Akhir

Kemampuan menghitung panjang sisi AC sangat penting untuk memahami hubungan sisi-sisi dalam segitiga siku-siku dan memiliki aplikasi yang luas dalam bidang arsitektur, teknik, dan desain. Dengan memahami konsep yang diuraikan dalam artikel ini, individu dapat secara efektif memanfaatkan pengetahuan ini untuk memecahkan masalah dan membuat keputusan yang tepat.

Pertanyaan Populer dan Jawabannya

Bagaimana cara menghitung panjang sisi AC menggunakan Teorema Pythagoras?

Dengan menggunakan rumus a² + b² = c², di mana a dan b adalah panjang sisi siku-siku dan c adalah panjang sisi miring (AC).

Apa manfaat mengetahui cara menghitung panjang sisi AC?

Memungkinkan perhitungan luas dan volume bangun ruang, desain struktur yang stabil, dan pemecahan masalah teknik yang melibatkan segitiga siku-siku.