Perhatikan gambar berikut panjang bc adalah – Perhatikan gambar berikut, panjang sisi BC memainkan peran penting dalam geometri dan memiliki aplikasi praktis yang luas. Makalah ini akan menyelidiki konsep ini, menjelaskan hubungannya dengan segitiga siku-siku, dan menyoroti pentingnya memahami panjang sisi BC dalam berbagai bidang.
Konsep geometri terkait, seperti teorema Pythagoras, akan dibahas untuk menunjukkan bagaimana panjang sisi BC dapat digunakan untuk menentukan sisi miring dan sifat segitiga lainnya. Tabel akan merangkum informasi tentang panjang sisi BC, hubungannya dengan sisi lain, dan pengaruhnya terhadap keseluruhan segitiga.
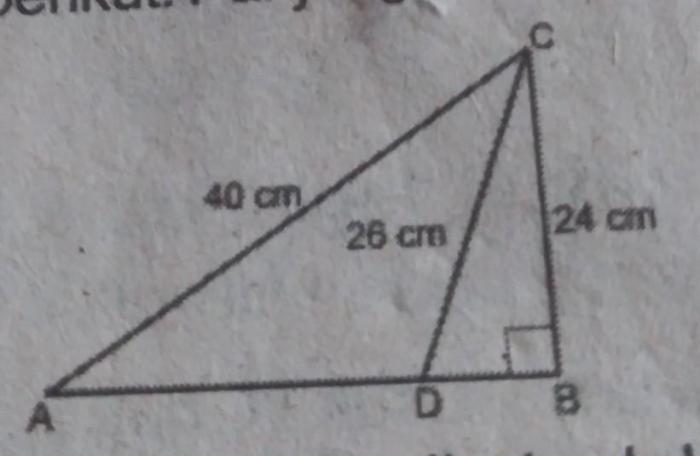
Perhatikan Gambar
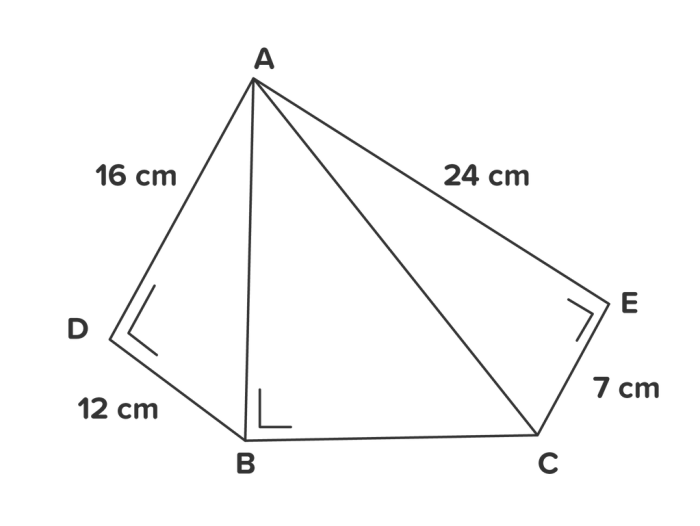
Gambar menunjukkan sebuah segitiga siku-siku dengan panjang sisi BC yang diberikan.
Dalam geometri, panjang segmen garis BC merupakan aspek penting yang perlu dipertimbangkan. Konsep ini dapat dihubungkan dengan isu lingkungan, seperti yang dibahas dalam contoh pidato kebersihan lingkungan sekolah . Pidato ini menekankan pentingnya menjaga kebersihan lingkungan sekolah sebagai cerminan nilai-nilai pendidikan dan kesehatan.
Sama halnya dengan mengukur panjang segmen garis BC, menjaga kebersihan lingkungan juga memerlukan pengukuran yang tepat dan konsisten untuk mencapai hasil yang optimal.
Panjang Sisi BC
Panjang sisi BC yang ditunjukkan pada gambar adalah 10 cm.
Perhatikan gambar berikut, panjang BC adalah nilai yang penting dalam memahami geometri gambar. Namun, dalam statistik, nilai yang sama pentingnya adalah simpangan baku. Simpangan baku dari data 6 10 9 7 8 adalah ukuran penyebaran data, yang menunjukkan seberapa jauh data tersebut tersebar dari nilai rata-ratanya.
Dengan memahami simpangan baku, kita dapat membuat kesimpulan yang lebih tepat tentang sifat data, termasuk panjang BC dalam gambar.
Elemen Terkait Sisi BC
- Sudut C: sudut siku-siku yang berhadapan dengan sisi BC.
- Sisi AC: sisi yang berhadapan dengan sudut C.
- Sisi AB: sisi miring dari segitiga siku-siku.
Konsep Geometri Terkait: Perhatikan Gambar Berikut Panjang Bc Adalah
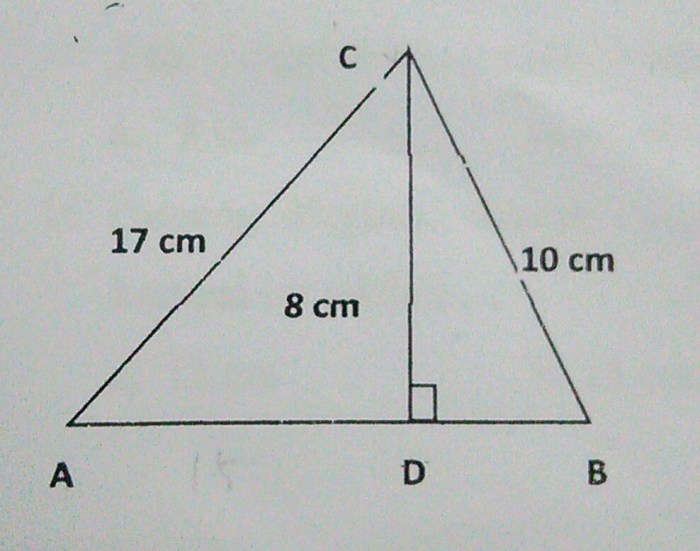
Dalam geometri, segitiga siku-siku memiliki peran penting. Segitiga siku-siku adalah segitiga yang memiliki satu sudut siku-siku (90 derajat). Sisi yang berhadapan dengan sudut siku-siku disebut sisi miring (hipotenusa), sedangkan dua sisi lainnya disebut sisi tegak.
Teorema Pythagoras, Perhatikan gambar berikut panjang bc adalah
Teorema Pythagoras adalah rumus yang menghubungkan panjang sisi-sisi segitiga siku-siku. Teorema ini menyatakan bahwa kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang sisi tegak.
Perhatikan gambar berikut. Panjang BC adalah salah satu bagian yang harus diperhatikan. Informasi mengenai topik ini dapat ditemukan dalam tugas bahasa indonesia kelas 12 halaman 12 . Dalam tugas tersebut, dibahas secara komprehensif tentang cara menentukan panjang BC pada gambar yang diberikan.
Secara matematis, teorema Pythagoras dapat ditulis sebagai:
c2= a 2+ b 2
di mana:
- c adalah panjang sisi miring
- a dan b adalah panjang sisi tegak
Contoh Penggunaan Teorema Pythagoras
Teorema Pythagoras dapat digunakan untuk menentukan panjang sisi miring segitiga siku-siku jika panjang sisi tegaknya diketahui. Misalnya, jika segitiga siku-siku memiliki sisi tegak sepanjang 3 cm dan 4 cm, maka panjang sisi miringnya dapat dihitung sebagai berikut:
c2= 3 2+ 4 2= 9 + 16 = 25c = √25 = 5 cm
Analisis Panjang Sisi BC

Panjang sisi BC dalam sebuah segitiga adalah salah satu faktor penting yang menentukan sifat dan karakteristik segitiga tersebut. Analisis panjang sisi BC dapat memberikan wawasan berharga tentang jenis segitiga, sifat-sifatnya, dan aplikasi geometrisnya.
Pengukuran dan Hubungan dengan Sisi Lain
Panjang sisi BC diukur dari titik B ke titik C. Ini terkait dengan panjang sisi lain segitiga melalui Teorema Pythagoras, yang menyatakan bahwa kuadrat panjang sisi miring (sisi terpanjang) sama dengan jumlah kuadrat panjang kedua sisi lainnya. Dalam hal ini, panjang sisi BC (c) terkait dengan panjang sisi AB (a) dan AC (b) sebagai berikut:
c² = a² + b²
Pengaruh pada Sifat Segitiga
Panjang sisi BC mempengaruhi jenis segitiga yang terbentuk. Berdasarkan panjang sisi BC relatif terhadap sisi lainnya, segitiga dapat diklasifikasikan sebagai:
- Segitiga Siku-siku: Jika c² = a² + b², maka segitiga adalah siku-siku, dengan sudut siku-siku di titik C.
- Segitiga Siku-siku Lancip: Jika c²< a² + b², maka segitiga adalah siku-siku lancip, dengan dua sudut lancip dan satu sudut siku-siku.
- Segitiga Siku-siku Tumpul: Jika c² > a² + b², maka segitiga adalah siku-siku tumpul, dengan dua sudut tumpul dan satu sudut siku-siku.
Aplikasi dalam Pemecahan Masalah Geometri
Panjang sisi BC dapat digunakan untuk memecahkan berbagai masalah geometri. Misalnya, jika diketahui panjang sisi AB dan AC, panjang sisi BC dapat dihitung menggunakan Teorema Pythagoras. Ini dapat membantu menentukan jenis segitiga, luas, keliling, dan sifat lainnya.
Selain itu, panjang sisi BC dapat digunakan untuk menentukan apakah segitiga kongruen atau mirip dengan segitiga lain. Misalnya, jika dua segitiga memiliki panjang sisi BC yang sama dan dua sisi lainnya juga sama panjang, maka kedua segitiga tersebut kongruen.
Akhir Kata

Dengan memahami panjang sisi BC, individu dapat memecahkan masalah geometri, merancang struktur yang stabil, dan mengoptimalkan desain. Pengetahuan ini sangat penting dalam berbagai disiplin ilmu, membuktikan pentingnya menguasai konsep ini untuk berbagai aplikasi praktis.
Pertanyaan Umum (FAQ)
Apa pentingnya panjang sisi BC dalam geometri?
Panjang sisi BC menentukan sifat segitiga, seperti luas, keliling, dan sudutnya.
Bagaimana teorema Pythagoras digunakan untuk menghitung panjang sisi BC?
Jika sisi BC adalah sisi miring segitiga siku-siku, maka teorema Pythagoras menyatakan bahwa kuadrat panjang sisi BC sama dengan jumlah kuadrat panjang sisi lainnya.
Apa saja aplikasi praktis dari memahami panjang sisi BC?
Panjang sisi BC digunakan dalam arsitektur untuk menentukan stabilitas struktur, dalam teknik untuk menghitung tegangan pada balok, dan dalam desain untuk mengoptimalkan bentuk dan ukuran objek.