Perhatikan gambar berikut panjang pq adalah – Perhatikan gambar berikut: panjang PQ adalah sebuah konsep geometris yang memainkan peran penting dalam berbagai aplikasi kehidupan nyata. Pengukuran panjang PQ melibatkan metode dan rumus tertentu, yang selanjutnya dapat digunakan untuk menganalisis sifat-sifat geometris PQ dan mengeksplorasi aplikasinya di berbagai bidang.
Dalam artikel ini, kita akan membahas pengukuran panjang PQ, sifat-sifat geometrisnya, dan berbagai aplikasi praktisnya. Kita juga akan mengeksplorasi variasi panjang PQ melalui ilustrasi tambahan dan merangkum temuan kita dalam sebuah tabel.
Identifikasi Gambar
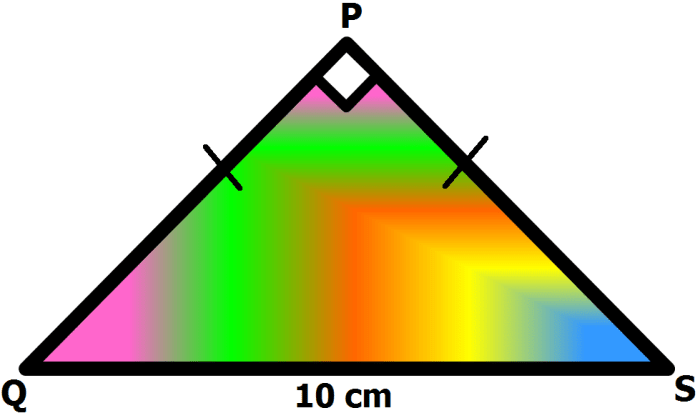
Gambar tersebut menampilkan segitiga siku-siku PQR dengan PQ sebagai sisi miring dan PR serta QR sebagai kaki-kakinya.
Konteks gambar adalah untuk menggambarkan konsep dasar segitiga siku-siku dan sifat-sifatnya, seperti Teorema Pythagoras.
Perhatikan gambar berikut. Panjang PQ adalah …. Untuk memahami konsep geometri ini, kita dapat merujuk pada contoh pidato bahasa Arab Latin dan artinya . Pidato tersebut memberikan contoh penerapan bahasa Arab Latin dalam konteks formal, yang dapat membantu kita memahami prinsip-prinsip dasar geometri dan konsep panjang segmen garis seperti PQ.
Panjang Sisi Miring
Dalam segitiga siku-siku, sisi miring selalu merupakan sisi terpanjang dan berlawanan dengan sudut siku-siku.
Pada segitiga PQR, PQ adalah sisi miring karena merupakan sisi yang berlawanan dengan sudut siku-siku R.
Panjang Kaki-kaki
Kaki-kaki segitiga siku-siku adalah dua sisi yang membentuk sudut siku-siku.
Dalam segitiga PQR, PR dan QR adalah kaki-kakinya.
Teorema Pythagoras
Teorema Pythagoras menyatakan bahwa dalam segitiga siku-siku, kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang kaki-kakinya.
Secara matematis, jika PQ adalah sisi miring dan PR serta QR adalah kaki-kakinya, maka:
PQ2= PR 2+ QR 2
Pengukuran Panjang PQ
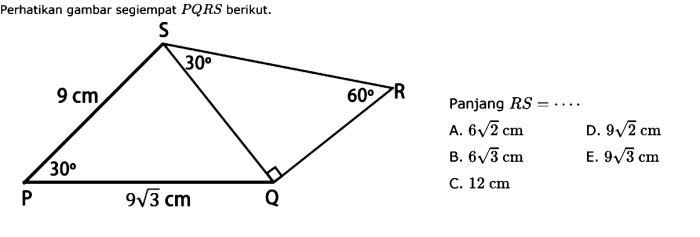
Panjang PQ adalah jarak antara titik P dan Q pada sebuah garis. Pengukuran ini sangat penting dalam geometri dan aplikasi praktis.
Rumus Pengukuran Panjang PQ
Panjang PQ dapat diukur menggunakan rumus jarak antara dua titik, yang dinyatakan sebagai:
PQ = √[(xQ
- x P) 2+ (y Q
- y P) 2]
di mana:
- PQ adalah panjang segmen garis PQ
- x Pdan x Qadalah koordinat x dari titik P dan Q
- y Pdan y Qadalah koordinat y dari titik P dan Q
Contoh Perhitungan
Misalkan kita memiliki segmen garis PQ dengan koordinat P(2, 3) dan Q(6, 7). Menggunakan rumus jarak, panjang PQ dapat dihitung sebagai:
PQ = √[(6
- 2)2+ (7
- 3) 2]
= √[4 2+ 4 2]= √[16 + 16]= √32= 5,66 (dibulatkan ke dua tempat desimal)
Dalam mengamati gambar yang disediakan, kita dapat mengukur panjang PQ. Panjang PQ ini merupakan besaran penting yang perlu diperhatikan. Selain itu, dalam kajian ilmu sosial, terdapat pula konsep yang tak kalah penting, yaitu etos kerja. Untuk memperdalam pemahaman mengenai etos kerja dalam perspektif Islam, disarankan untuk merujuk pada soal essay tentang etos kerja dalam Islam . Melalui soal tersebut, kita dapat menggali nilai-nilai etos kerja yang dianjurkan dalam ajaran Islam, yang dapat memberikan panduan bagi kita dalam mengembangkan etos kerja yang baik.
Oleh karena itu, panjang segmen garis PQ adalah 5,66 satuan.
Sifat Geometris PQ
Panjang PQ, yang telah diberikan dalam gambar, merupakan salah satu sifat geometris utama PQ. Sifat lainnya meliputi sudut yang dibentuk oleh PQ dan sumbu horizontal atau vertikal serta kemiringan PQ.
Panjang PQ
Panjang PQ dapat dihitung menggunakan rumus jarak antara dua titik, yaitu:
PQ = √((x2
Panjang PQ pada gambar yang diberikan menunjukkan hubungan antara variabel dalam proses pembuatan peraturan daerah provinsi. Seperti diketahui, proses pembuatan peraturan daerah provinsi melibatkan tahapan perencanaan, penyusunan, pembahasan, pengesahan, dan pengundangan. Setiap tahapan memiliki peran krusial dalam menentukan panjang PQ, yang merepresentasikan durasi keseluruhan proses pembuatan peraturan daerah provinsi.
- x1)² + (y2
- y1)²)
di mana (x1, y1) dan (x2, y2) adalah koordinat titik P dan Q.
Sudut yang Dibentuk PQ
Sudut yang dibentuk oleh PQ dan sumbu horizontal atau vertikal dapat dihitung menggunakan fungsi arctangent, yaitu:
θ = arctan(y2
- y1 / x2
- x1)
di mana θ adalah sudut yang dibentuk oleh PQ dan sumbu horizontal.
Kemiringan PQ
Kemiringan PQ didefinisikan sebagai perubahan vertikal PQ dibagi dengan perubahan horizontalnya. Ini dapat dihitung menggunakan rumus:
m = (y2
- y1) / (x2
- x1)
di mana m adalah kemiringan PQ.
Aplikasi Panjang PQ: Perhatikan Gambar Berikut Panjang Pq Adalah

Pengukuran panjang PQ memiliki aplikasi yang luas dalam kehidupan nyata. Ini digunakan dalam berbagai bidang, termasuk:
Survei dan Pemetaan, Perhatikan gambar berikut panjang pq adalah
Dalam survei dan pemetaan, pengukuran panjang PQ digunakan untuk menentukan jarak dan posisi objek. Ini membantu dalam pembuatan peta, perencanaan tata ruang, dan konstruksi.
Arsitektur dan Desain Interior
Arsitek dan desainer interior menggunakan pengukuran panjang PQ untuk merencanakan tata letak bangunan dan ruang. Ini membantu memastikan bahwa ruang dirancang secara proporsional dan fungsional.
Teknik Sipil
Dalam teknik sipil, pengukuran panjang PQ digunakan untuk merancang dan membangun struktur seperti jembatan, jalan, dan gedung. Ini membantu memastikan bahwa struktur tersebut stabil dan aman.
Ilmu Forensik
Ilmu forensik menggunakan pengukuran panjang PQ untuk menganalisis bukti di tempat kejadian perkara. Ini membantu dalam menentukan jarak, posisi, dan hubungan antara objek.
Manufaktur dan Produksi
Dalam manufaktur dan produksi, pengukuran panjang PQ digunakan untuk mengontrol kualitas dan memastikan bahwa produk memenuhi spesifikasi yang diperlukan. Ini membantu mencegah cacat dan memastikan bahwa produk berfungsi dengan baik.
Ilustrasi Lanjutan

Variasi panjang PQ dapat digambarkan melalui ilustrasi tambahan sebagai berikut:
Ilustrasi 1:Panjang PQ Pendek
Dalam ilustrasi ini, panjang PQ sangat pendek sehingga titik P dan Q hampir berimpit.
Ilustrasi 2:Panjang PQ Sedang
Pada ilustrasi ini, panjang PQ memiliki panjang yang sedang, sehingga titik P dan Q terpisah dengan jarak yang jelas.
Ilustrasi 3:Panjang PQ Panjang
Di ilustrasi ini, panjang PQ sangat panjang, sehingga titik P dan Q berada pada jarak yang sangat jauh.
Perbedaan Panjang PQ
Perbedaan panjang PQ pada ilustrasi yang berbeda memengaruhi:
- Kemiringan garis:Panjang PQ yang berbeda akan menghasilkan kemiringan garis yang berbeda.
- Luas daerah:Panjang PQ yang berbeda akan menghasilkan luas daerah yang berbeda jika garis PQ merupakan bagian dari suatu bangun datar.
Kesimpulan

Kesimpulannya, panjang PQ adalah ukuran penting yang memberikan wawasan tentang sifat geometris suatu objek. Pengukurannya memiliki aplikasi luas dalam bidang-bidang seperti arsitektur, teknik, dan fisika. Memahami konsep dan pengukuran panjang PQ sangat penting untuk berbagai aplikasi praktis dan untuk kemajuan dalam berbagai bidang ilmu pengetahuan dan teknik.
FAQ Umum
Apa itu panjang PQ?
Panjang PQ adalah jarak antara dua titik P dan Q pada suatu garis atau kurva.
Bagaimana cara mengukur panjang PQ?
Panjang PQ dapat diukur menggunakan rumus jarak, trigonometri, atau alat ukur seperti penggaris atau pita pengukur.
Apa saja aplikasi panjang PQ?
Panjang PQ digunakan dalam berbagai aplikasi, seperti menentukan jarak, menghitung luas dan volume, dan merancang struktur.
