Persamaan garis pada gambar berikut adalah – Persamaan garis pada gambar merupakan representasi matematis dari garis yang ditampilkan dalam suatu gambar. Menentukan persamaan garis dari gambar sangat penting untuk berbagai aplikasi, mulai dari geometri hingga fisika.

Dalam artikel ini, kita akan mengeksplorasi cara menentukan persamaan garis dari gambar, jenis-jenis persamaan garis, dan contoh penerapannya dalam kehidupan nyata.

Persamaan Garis pada Gambar

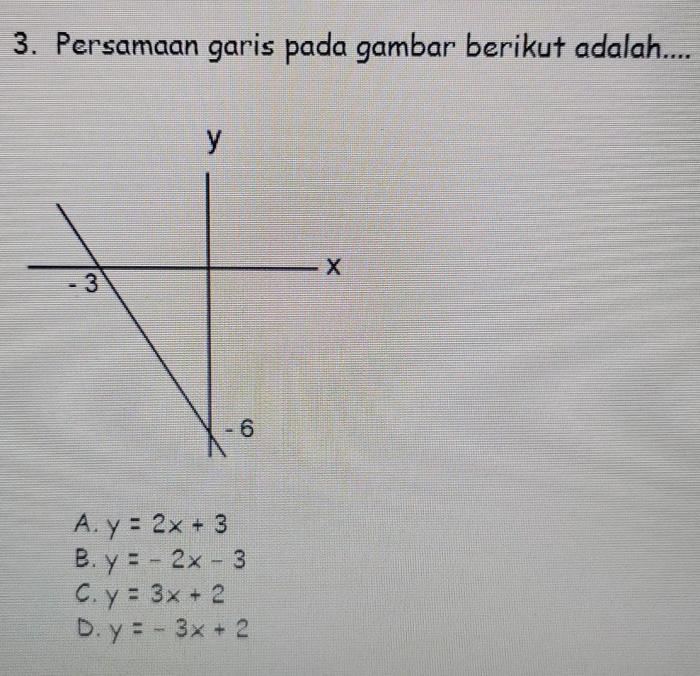
Persamaan garis adalah persamaan matematika yang menggambarkan hubungan antara dua variabel, biasanya dilambangkan sebagai x dan y. Dalam sebuah gambar, garis dapat diwakili oleh grafik yang menghubungkan titik-titik data.

Identifikasi Garis pada Gambar

Langkah pertama dalam menentukan persamaan garis dari gambar adalah mengidentifikasi garis yang dimaksud. Garis ini dapat berupa garis lurus, garis lengkung, atau garis yang dibentuk oleh sekumpulan titik.

Menentukan Gradien Garis

Gradien garis adalah nilai yang menunjukkan kemiringan garis. Gradien dapat ditentukan dari gambar dengan menggunakan dua titik pada garis tersebut. Gradien dihitung dengan menggunakan rumus berikut:

m = (y2

• y1) / (x2
• x1)

di mana:

• m adalah gradien garis
• x1 dan y1 adalah koordinat titik pertama
• x2 dan y2 adalah koordinat titik kedua

Menentukan Persamaan Garis

Setelah gradien garis diketahui, persamaan garis dapat ditentukan dengan menggunakan titik apa pun pada garis tersebut dan gradien. Persamaan garis dapat ditulis dalam bentuk y = mx + c, di mana:

• m adalah gradien garis
• c adalah titik potong garis dengan sumbu y

Titik potong y dapat ditentukan dengan mensubstitusikan titik pada garis ke dalam persamaan garis.

Contoh

Misalkan kita memiliki gambar yang menunjukkan garis lurus yang melewati titik (2, 3) dan (5, 7). Untuk menentukan persamaan garis ini, kita dapat mengikuti langkah-langkah berikut:

1. Menghitung gradien: m = (7
   • 3) / (5
   • 2) = 4/3
2. Mensubstitusikan titik (2, 3) dan gradien ke dalam persamaan garis: 3 = (4/3)
   

   2 + c

3. Menyelesaikan untuk c: c = 1

Jadi, persamaan garis yang mewakili garis pada gambar adalah y = (4/3)x + 1.

Jenis-jenis Persamaan Garis

Persamaan garis dapat diklasifikasikan menjadi beberapa jenis berdasarkan bentuknya. Berikut adalah tiga jenis persamaan garis yang umum digunakan:

Bentuk Lereng-Intercept

Bentuk lereng-intercept dari persamaan garis ditulis sebagai y = mx + b, di mana:

• madalah kemiringan garis, yang menunjukkan arah dan kecuraman garis.
• badalah titik potong y, yang menunjukkan titik di mana garis memotong sumbu y.

Bentuk Titik-Lereng

Bentuk titik-lereng dari persamaan garis ditulis sebagai y- y ₁= m(x – x ₁) , di mana:

• ( x₁, y₁) adalah titik yang terletak pada garis.
• madalah kemiringan garis.

Bentuk Standar

Bentuk standar dari persamaan garis ditulis sebagai Ax + By = C, di mana:

• A, B, dan Cadalah konstanta.
• Adan Btidak boleh keduanya nol.

Setiap jenis persamaan garis memiliki kegunaan dan keunggulannya masing-masing dalam konteks aplikasi yang berbeda.

Contoh dan Cara Penentuan Persamaan Garis

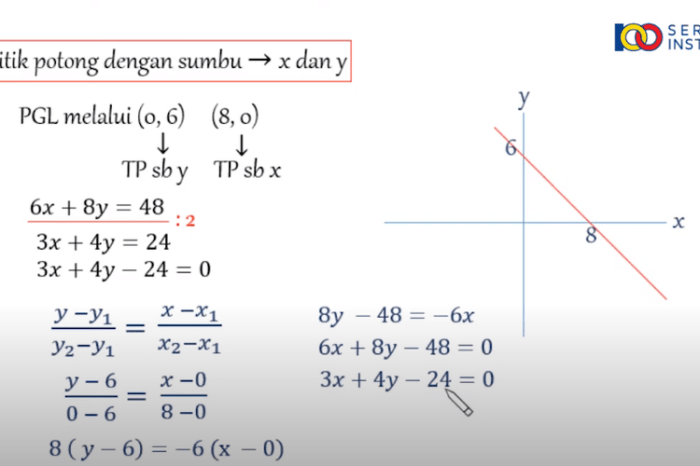
Persamaan garis dapat ditentukan melalui beberapa metode, salah satunya adalah dengan menggunakan gambar. Berikut adalah beberapa contoh gambar garis dan cara menentukan persamaannya:

Contoh 1: Garis Melalui Dua Titik

• Misalkan kita memiliki garis yang melalui titik (2, 3) dan (5, 7).
• Perbedaan koordinat y dan x dari titik-titik tersebut adalah 7 – 3 = 4 dan 5 – 2 = 3.
• Gradien (m) garis tersebut adalah 4/3.
• Persamaan garis tersebut dapat ditulis dalam bentuk y – y1 = m(x – x1), di mana (x1, y1) adalah salah satu titik yang diketahui.
• Menggunakan titik (2, 3) sebagai (x1, y1), persamaan garis tersebut menjadi y – 3 = (4/3)(x – 2).

Contoh 2: Garis Paralel Sumbu X

• Misalkan kita memiliki garis paralel sumbu x yang melalui titik (3, 2).
• Gradien garis tersebut adalah 0 karena tidak memiliki kemiringan.
• Persamaan garis tersebut dapat ditulis dalam bentuk y = b, di mana b adalah konstanta yang mewakili nilai y-intercept.
• Menggunakan titik (3, 2) sebagai titik yang diketahui, persamaan garis tersebut menjadi y = 2.

Contoh 3: Garis Tegak Lurus Sumbu Y

• Misalkan kita memiliki garis tegak lurus sumbu y yang melalui titik (4, 3).
• Gradien garis tersebut tidak terdefinisi karena tidak memiliki kemiringan.
• Persamaan garis tersebut dapat ditulis dalam bentuk x = a, di mana a adalah konstanta yang mewakili nilai x-intercept.
• Menggunakan titik (4, 3) sebagai titik yang diketahui, persamaan garis tersebut menjadi x = 4.

Aplikasi Persamaan Garis dalam Kehidupan Nyata

Persamaan garis merupakan alat matematika yang ampuh yang memiliki banyak aplikasi dalam kehidupan nyata. Dari menentukan jarak hingga menghitung kecepatan, persamaan garis dapat digunakan untuk memecahkan berbagai masalah praktis.

Menentukan Jarak, Persamaan garis pada gambar berikut adalah

Persamaan garis dapat digunakan untuk menentukan jarak antara dua titik. Misalnya, jika kita memiliki persamaan garis y = 2x + 1 dan kita ingin menemukan jarak antara titik (1, 3) dan (3, 7), kita dapat menggunakan rumus jarak:

Jarak = √((x2 – x1)^2 + (y2 – y1)^2)

Dengan mengganti nilai-nilai titik ke dalam rumus, kita mendapatkan:

Jarak = √((3 – 1)^2 + (7 – 3)^2)

Persamaan garis pada gambar berikut adalah representasi matematis dari hubungan antara dua titik pada garis tersebut. Konsep ini juga berlaku dalam rangkaian lampu kepala mobil dengan relay , di mana persamaan garis digunakan untuk menentukan resistansi dan tegangan dalam rangkaian.

Pemahaman tentang persamaan garis sangat penting untuk menganalisis dan merancang sistem kelistrikan secara akurat, termasuk rangkaian lampu kepala mobil.

Jarak = √(4 + 16)

Jarak = √20

Persamaan garis pada gambar berikut adalah y = mx + b, di mana m adalah gradien dan b adalah titik potong y. Dari hasil survei diketahui bahwa ternyata preferensi masyarakat terhadap gradien garis bervariasi . Hal ini memengaruhi nilai m dalam persamaan garis, sehingga persamaan garis dapat berbeda-beda sesuai dengan preferensi yang diamati dalam survei tersebut.

Jarak = 4,47

Jadi, jarak antara titik (1, 3) dan (3, 7) adalah 4,47 satuan.

Menghitung Kecepatan

Persamaan garis juga dapat digunakan untuk menghitung kecepatan. Misalnya, jika kita memiliki persamaan garis y = 50t + 100, di mana t mewakili waktu dan y mewakili jarak, kita dapat menemukan kecepatan dengan mencari gradien garis.

Persamaan garis pada gambar berikut adalah y = mx + c. Untuk memahami konsep persamaan garis, kita dapat mempelajari contoh soal perang dunia 1 beserta jawaban . Dari contoh soal tersebut, kita dapat memahami bagaimana persamaan garis digunakan dalam konteks sejarah untuk menganalisis tren dan peristiwa.

Dengan mengaplikasikan pemahaman ini pada persamaan garis pada gambar, kita dapat memperoleh wawasan tentang hubungan antara variabel yang digambarkan oleh garis tersebut.

Gradien = (y2 – y1) / (x2 – x1)

Dengan memilih dua titik sembarang pada garis, misalnya (0, 100) dan (1, 150), kita mendapatkan:

Gradien = (150 – 100) / (1 – 0)

Gradien = 50

Jadi, kecepatannya adalah 50 satuan per satuan waktu.

Ringkasan Penutup

Persamaan garis merupakan alat yang ampuh untuk mewakili dan menganalisis garis. Memahami cara menentukan dan menggunakan persamaan garis sangat penting untuk berbagai bidang, seperti matematika, sains, dan teknik.

Pertanyaan Umum (FAQ): Persamaan Garis Pada Gambar Berikut Adalah

Bagaimana cara menentukan persamaan garis dari gambar?

Tentukan dua titik pada garis, hitung gradien, dan gunakan rumus titik-lereng untuk membuat persamaan.

Apa saja jenis-jenis persamaan garis?

Persamaan lereng-intercept, persamaan titik-lereng, dan persamaan standar.

Apa saja aplikasi persamaan garis dalam kehidupan nyata?

Menentukan jarak, kecepatan, dan kemiringan benda.