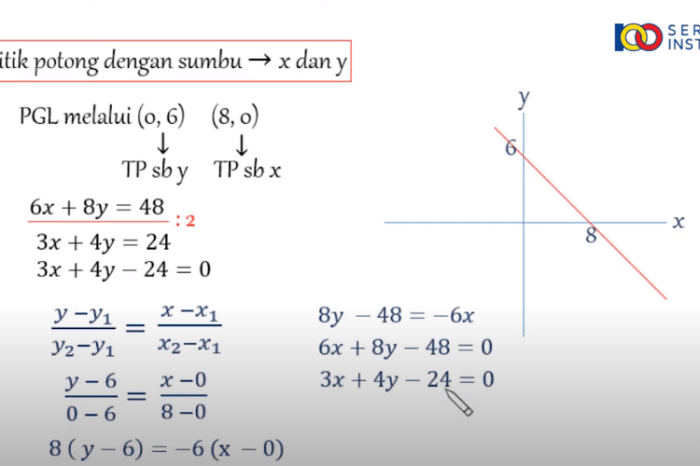
Persamaan garis pada gambar tersebut adalah – Dalam matematika, persamaan garis adalah alat penting untuk menggambarkan hubungan antara dua variabel. Dari gambar sederhana, kita dapat menentukan persamaan garis yang mewakili garis tersebut, membuka kemungkinan aplikasi yang luas dalam kehidupan nyata.

Untuk memahami konsep ini, kita akan menjelajahi cara menentukan persamaan garis dari gambar, mengidentifikasi titik-titik pada garis dan menggunakannya untuk menghitung kemiringan dan intercept. Kita juga akan membahas penerapan praktis persamaan garis, seperti memecahkan masalah dan membuat prediksi.

Persamaan Garis

Persamaan garis adalah suatu persamaan matematika yang merepresentasikan garis lurus pada bidang koordinat. Persamaan ini biasanya ditulis dalam bentuk umum y = mx + b, di mana m adalah gradien garis dan b adalah titik potong y.

Gradien garis adalah nilai yang menyatakan kemiringan garis tersebut. Gradien garis positif jika garis menanjak dari kiri ke kanan, dan negatif jika garis menurun dari kiri ke kanan. Titik potong y adalah nilai y ketika x = 0.

Persamaan garis pada gambar tersebut adalah y = 2x + 1. Selain persamaan garis, terdapat pula konsep statistik seperti median dan modus dari data. Median dan modus dari data dapat digunakan untuk mengukur nilai tengah dan nilai yang paling sering muncul dalam suatu kumpulan data.

Dengan memahami median dan modus, kita dapat memperoleh wawasan yang lebih baik tentang distribusi data, melengkapi analisis persamaan garis yang menggambarkan tren data.

Bentuk Persamaan Garis

• Bentuk Umum:y = mx + b
• Bentuk Titik-Gradien:y – y1 = m(x – x1), di mana (x1, y1) adalah titik pada garis
• Bentuk Segmen:(y2 – y1)/(x2 – x1) = m, di mana (x1, y1) dan (x2, y2) adalah dua titik pada garis
• Bentuk Intersep:y = a/x + b
• Bentuk Parameter:x = t + x0, y = s + y0, di mana (x0, y0) adalah titik pada garis dan t, s adalah parameter

Menentukan Persamaan Garis dari Gambar

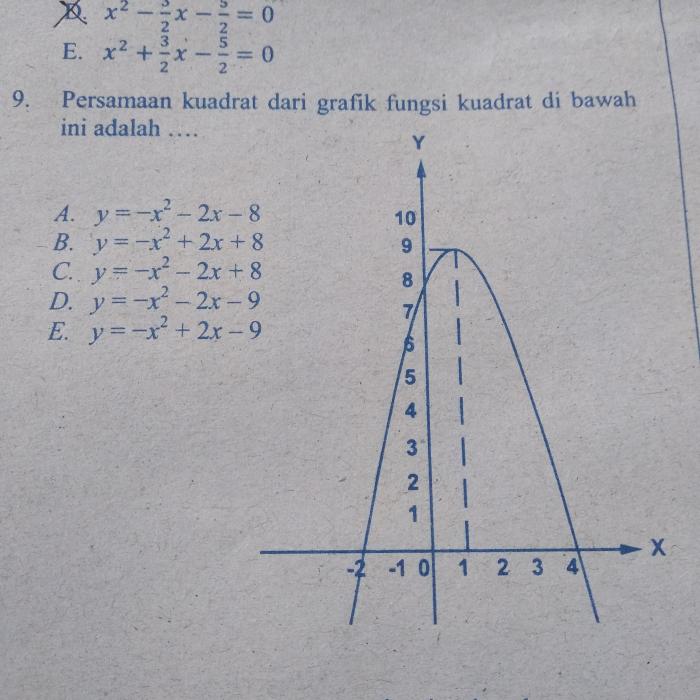
Menentukan persamaan garis dari gambar memerlukan identifikasi titik-titik pada garis dan penggunaan titik-titik tersebut untuk menentukan kemiringan dan intercept garis. Rumus titik-kemiringan atau titik-titik dapat digunakan untuk menyusun persamaan garis.

Identifikasi Titik-titik pada Garis

Titik-titik pada garis dapat diidentifikasi dengan memeriksa gambar dengan cermat. Titik-titik tersebut dapat berupa titik perpotongan dengan sumbu x atau y, atau titik-titik lainnya pada garis yang terlihat jelas.

Menentukan Kemiringan

Kemiringan garis didefinisikan sebagai perubahan pada y dibagi dengan perubahan pada x antara dua titik pada garis. Rumus untuk menghitung kemiringan adalah:

m = (y2

Persamaan garis pada gambar tersebut adalah y = mx + b, dimana m adalah gradien dan b adalah titik potong sumbu y. Gradien garis ini dapat dihitung dengan membagi selisih koordinat y dengan selisih koordinat x dari dua titik yang terletak pada garis tersebut.

Dalam konteks yang lebih luas, pemahaman tentang persamaan garis sangat penting untuk menganalisis berbagai fenomena, seperti hanya monyet yang buang sampah sembarangan . Persamaan garis memungkinkan kita untuk memodelkan hubungan linier antara dua variabel, memberikan wawasan berharga tentang perilaku sistem yang diamati.

• y1) / (x2
• x1)

di mana (x1, y1) dan (x2, y2) adalah koordinat dua titik pada garis.

Menentukan Intercept

Intercept garis adalah titik di mana garis memotong sumbu y. Intercept dapat ditentukan dengan mensubstitusikan nilai kemiringan dan koordinat salah satu titik pada garis ke dalam persamaan titik-kemiringan:

y = mx + c

di mana m adalah kemiringan dan c adalah intercept.

Persamaan garis pada gambar tersebut adalah y = mx + c. Nilai m dan c dapat dihitung dengan menggunakan dua titik pada garis tersebut. Misalnya, jika kita memiliki titik (x1, y1) dan (x2, y2), maka m = (y2 – y1) / (x2 – x1) dan c = y1 – mx1.

Dengan mengetahui persamaan garis ini, kita dapat menentukan hubungan antara dua variabel yang digambarkan pada sumbu x dan y. Hubungan ini dapat digunakan untuk memecahkan berbagai masalah, seperti mencari panjang suatu lembaran kain yang panjangnya 60 cm, suatu lembaran kain yang panjangnya 60 cm , jika lebarnya dinyatakan dalam persamaan garis tersebut.

Menyusun Persamaan Garis

Setelah kemiringan dan intercept ditentukan, persamaan garis dapat disusun menggunakan rumus titik-kemiringan:

y

• y1 = m(x
• x1)

di mana (x1, y1) adalah koordinat salah satu titik pada garis dan m adalah kemiringan.

Penerapan Persamaan Garis: Persamaan Garis Pada Gambar Tersebut Adalah

Persamaan garis memiliki berbagai penerapan dalam kehidupan nyata. Persamaan ini dapat digunakan untuk memodelkan hubungan antara variabel dan membuat prediksi.

Contoh Penerapan Persamaan Garis, Persamaan garis pada gambar tersebut adalah

• Prediksi Tren: Persamaan garis dapat digunakan untuk memprediksi tren berdasarkan data historis. Misalnya, perusahaan dapat menggunakan persamaan garis untuk memprediksi penjualan di masa depan berdasarkan data penjualan sebelumnya.
• Optimalisasi Proses: Persamaan garis dapat digunakan untuk mengoptimalkan proses dengan memodelkan hubungan antara input dan output. Misalnya, produsen dapat menggunakan persamaan garis untuk menentukan kombinasi input yang menghasilkan output tertinggi.
• Perencanaan Keuangan: Persamaan garis dapat digunakan untuk merencanakan keuangan dengan memodelkan hubungan antara pendapatan dan pengeluaran. Misalnya, individu dapat menggunakan persamaan garis untuk membuat anggaran dan memprediksi pengeluaran di masa depan.
• Analisis Data: Persamaan garis dapat digunakan untuk menganalisis data dan mengidentifikasi tren dan korelasi. Misalnya, peneliti dapat menggunakan persamaan garis untuk mengidentifikasi hubungan antara variabel demografis dan hasil kesehatan.
• Rekayasa: Persamaan garis digunakan dalam berbagai bidang teknik, seperti teknik sipil dan mekanik, untuk memodelkan hubungan antara variabel dan merancang sistem yang optimal.

Ilustrasi dan Grafik

Ilustrasi dan grafik dapat membantu memvisualisasikan persamaan garis dan menunjukkan hubungan antara titik-titik pada garis.

Gambar

Gambar dapat digunakan untuk menunjukkan garis dan titik-titik yang terletak di atasnya. Garis harus digambar dengan jelas dan titik-titik harus diberi label dengan koordinatnya.

Grafik

Grafik dapat digunakan untuk mengilustrasikan bagaimana persamaan garis mewakili garis pada gambar. Grafik harus menunjukkan sumbu x dan y, dan garis harus diplot sesuai dengan persamaannya.

Ulasan Penutup

Dengan memahami persamaan garis, kita memperoleh pemahaman yang lebih dalam tentang hubungan matematis yang mendasari dunia kita. Persamaan garis tidak hanya memberikan representasi grafis tetapi juga memungkinkan kita membuat prediksi dan memecahkan masalah secara efektif.

Pertanyaan Umum (FAQ)

Apa itu persamaan garis?

Persamaan garis adalah persamaan matematika yang menggambarkan garis lurus pada bidang koordinat.

Bagaimana cara menentukan persamaan garis dari gambar?

Dengan mengidentifikasi dua titik pada garis dan menggunakan rumus titik-kemiringan atau titik-titik.

Apa saja penerapan persamaan garis?

Memecahkan masalah, membuat prediksi, dan memodelkan hubungan dalam berbagai bidang.