Dalam ranah geometri, elips, kurva tertutup yang anggun, telah memikat para matematikawan selama berabad-abad. Persamaan garis singgungnya, yang menentukan garis lurus yang menyentuh elips pada titik tertentu, memainkan peran penting dalam mengungkap sifat geometris yang menakjubkan dari bentuk ini.

Pemahaman tentang persamaan garis singgung elips tidak hanya terbatas pada ranah teoretis tetapi juga menemukan aplikasi praktis yang luas, seperti dalam desain arsitektur, analisis data, dan banyak lagi. Artikel ini akan menelusuri persamaan ini secara mendalam, mengeksplorasi metodenya, aplikasi, dan signifikansinya dalam bidang matematika dan di luarnya.

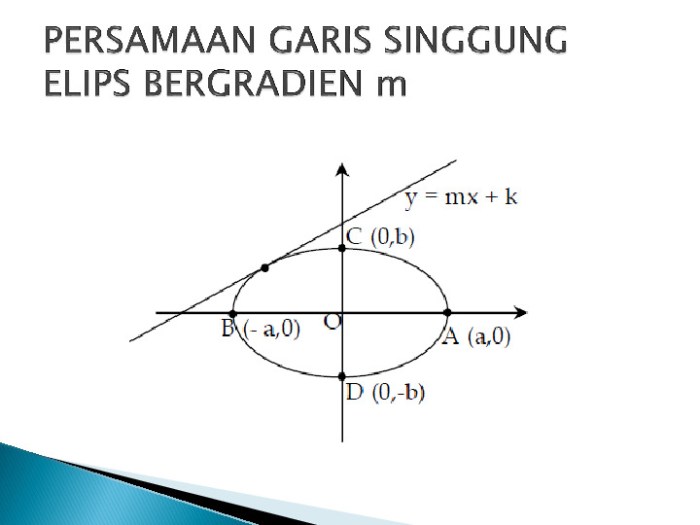
Persamaan Umum Garis Singgung Elips

Persamaan umum garis singgung elips adalah persamaan garis lurus yang menyinggung elips di suatu titik tertentu.

Misalkan elips memiliki persamaan:

$$ \fracx^2a^2 + \fracy^2b^2 = 1 $$

Dan garis singgung menyinggung elips di titik (x ₀ , y ₀ ), maka persamaan garis singgung tersebut adalah:

$$ xx_0 \fraca^2b^2 + yy_0 = a^2 $$

Contoh

Misalkan elips memiliki persamaan:

$$ \fracx^29 + \fracy^24 = 1 $$

Dan garis singgung menyinggung elips di titik (3, 2), maka persamaan garis singgung tersebut adalah:

$$ 3x \frac94 + 2y = 9 $$$$ \Rightarrow 3x + \frac8y4 = 9 $$$$ \Rightarrow 3x + 2y = 9 $$

Aplikasi Persamaan Garis Singgung Elips

Persamaan garis singgung elips memiliki aplikasi yang luas dalam berbagai bidang, seperti matematika, fisika, dan teknik.

Aplikasi dalam Matematika

• Mencari titik-titik perpotongan antara dua elips.
• Mencari kemiringan garis normal terhadap elips di titik tertentu.
• Mencari persamaan garis singgung pada elips yang sejajar atau tegak lurus dengan garis tertentu.

Aplikasi dalam Fisika

• Menghitung lintasan benda yang bergerak dalam medan gravitasi, seperti orbit planet atau lintasan proyektil.
• Memodelkan getaran benda elastis, seperti pegas atau membran.
• Menghitung refleksi dan refraksi cahaya pada permukaan elips, seperti cermin atau lensa.

Aplikasi dalam Teknik

• Merancang lintasan kendaraan yang optimal pada tikungan.
• Membuat kurva pada permukaan objek, seperti desain bodi mobil atau sayap pesawat.
• Menganalisis gaya dan tegangan pada struktur elips, seperti jembatan atau gedung.

Contoh Soal dan Pembahasan

Untuk memahami penerapan persamaan garis singgung elips, berikut ini adalah contoh soal dan pembahasannya:

Soal

Tentukan persamaan garis singgung elips 9x ² + 16y ² = 144 pada titik (3, 2) .

Pembahasan

Langkah-langkah menentukan persamaan garis singgung elips:

1. Tentukan gradien garis normal pada titik singgung.
2. Tentukan gradien garis singgung sebagai invers negatif dari gradien garis normal.
3. Tentukan persamaan garis singgung menggunakan titik singgung dan gradien.

1. Gradien Garis Normal

Gradien garis normal pada titik (x ₀ , y ₀ ) pada elips Ax ² + By ² = C diberikan oleh:

m _normal = – (Ax ₀ /By ₀ )

Untuk elips yang diberikan, gradien garis normal pada titik (3, 2) adalah:

m _normal = – (9(3)/16(2)) = -27/32

2. Gradien Garis Singgung

Gradien garis singgung adalah invers negatif dari gradien garis normal:

m _singgung = -1/m _normal = 32/27

3. Persamaan Garis Singgung

Persamaan garis singgung menggunakan titik singgung (3, 2) dan gradien 32/27 adalah:

y – 2 = (32/27)(x – 3)

32x – 96 = 27y – 54

32x – 27y = 42

Jadi, persamaan garis singgung elips pada titik (3, 2) adalah 32x – 27y = 42 .

Kesimpulan

Persamaan garis singgung elips memberikan wawasan yang berharga tentang perilaku elips dan memungkinkan kita untuk mengungkap sifat geometrisnya yang tersembunyi. Dari aplikasi praktisnya dalam desain hingga peran fundamentalnya dalam analisis matematis, persamaan ini terus menjadi alat yang tak ternilai dalam gudang pengetahuan kita.

Memahaminya membuka pintu bagi pemahaman yang lebih dalam tentang dunia bentuk dan simetri, mengungkapkan keindahan dan kekuatan matematika.

Tanya Jawab (Q&A)

Apa itu persamaan garis singgung elips?

Persamaan garis singgung elips adalah persamaan yang mendefinisikan garis lurus yang menyentuh elips pada titik tertentu.

Bagaimana cara menentukan persamaan garis singgung elips?

Persamaan garis singgung elips dapat ditentukan dengan menggunakan gradien elips pada titik singgung dan koordinat titik tersebut.

Apa saja aplikasi persamaan garis singgung elips?

Persamaan garis singgung elips memiliki aplikasi dalam berbagai bidang, seperti desain arsitektur, analisis data, dan optimasi.