Dalam geometri, garis singgung sejajar memegang peranan penting dalam memahami sifat-sifat lingkaran. Garis ini merupakan garis yang menyentuh lingkaran pada satu titik dan sejajar dengan garis singgung lainnya pada titik yang berbeda. Pembahasan mengenai persamaan garis singgung sejajar ini akan mengeksplorasi konsep, metode penentuan, dan aplikasinya yang luas.

Konsep garis singgung sejajar dapat diilustrasikan melalui contoh sederhana. Misalkan kita memiliki sebuah lingkaran dengan pusat di titik (0,0) dan jari-jari r. Jika kita menggambar dua garis singgung pada lingkaran tersebut pada titik A dan B, maka garis AB akan menjadi garis singgung sejajar.

Pengertian Garis Singgung Sejajar

Contoh Garis Singgung Sejajar

Misalkan kita memiliki sebuah lingkaran dengan pusat di titik (0, 0) dan jari-jari r. Garis singgung yang sejajar dengan sumbu x dapat dinyatakan dengan persamaan y = ±r.

Persamaan Garis Singgung Sejajar

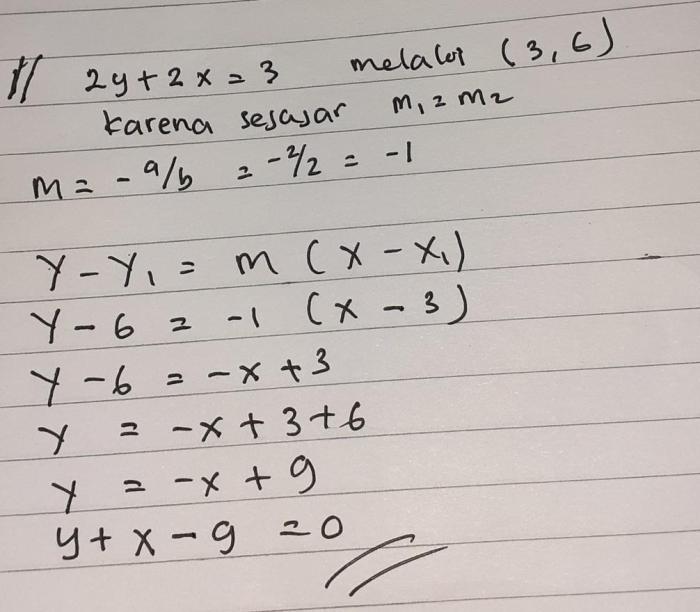
Garis singgung sejajar adalah garis singgung yang memiliki kemiringan sama dengan kemiringan jari-jari yang ditarik dari pusat lingkaran ke titik singgung. Persamaan umum garis singgung sejajar dapat disusun sebagai berikut:y

• y₁ = m(x
• x₁)

di mana (x₁, y₁) adalah koordinat titik singgung dan m adalah kemiringan jari-jari.

Tabel Persamaan Garis Singgung Sejajar

Berikut adalah tabel yang merangkum persamaan garis singgung sejajar berdasarkan posisi relatifnya terhadap pusat lingkaran:

Posisi	Persamaan
Sejajar sumbu x di atas pusat	y = k
Sejajar sumbu x di bawah pusat	y = k
Sejajar sumbu y di kanan pusat	x = h
Sejajar sumbu y di kiri pusat	x = h

Catatan:

• h adalah jarak horizontal dari pusat lingkaran ke garis singgung.
• k adalah jarak vertikal dari pusat lingkaran ke garis singgung.

Cara Menentukan Persamaan Garis Singgung Sejajar

Untuk menentukan persamaan garis singgung sejajar dengan suatu lingkaran, ikuti langkah-langkah berikut:

Menentukan Titik Singgung

Titik singgung adalah titik di mana garis singgung bersentuhan dengan lingkaran. Untuk menentukan titik singgung, kita dapat menggunakan persamaan lingkaran dan garis lurus yang mewakili garis singgung.

Misalkan persamaan lingkaran adalah:

“`(x

• h)² + (y
• k)² = r²

“`

dan persamaan garis lurus yang mewakili garis singgung adalah:

“`y = mx + c“`

Substitusikan persamaan garis lurus ke dalam persamaan lingkaran untuk mendapatkan persamaan kuadrat dalam x.

Pecahkan persamaan kuadrat tersebut untuk mendapatkan nilai x dari titik singgung. Setelah mendapatkan nilai x, substitusikan kembali ke dalam persamaan garis lurus untuk mendapatkan nilai y titik singgung.

Menentukan Gradien Garis Singgung

Gradien garis singgung sejajar dengan jari-jari lingkaran yang ditarik dari pusat lingkaran ke titik singgung. Gradien jari-jari lingkaran adalah:

“`m = (y

• k) / (x
• h)

“`

di mana (h, k) adalah pusat lingkaran.

Menentukan Persamaan Garis Singgung

Dengan mengetahui titik singgung (x₁, y₁) dan gradien m, persamaan garis singgung dapat ditentukan menggunakan persamaan titik-gradien:

“`y

• y₁ = m(x
• x₁)

“`

Aplikasi Garis Singgung Sejajar

Garis singgung sejajar memiliki berbagai aplikasi di berbagai bidang, termasuk geometri, fisika, dan teknik.

Geometri

• Menentukan persamaan garis singgung suatu kurva pada titik tertentu.
• Mencari titik-titik potong antara dua kurva.
• Menentukan kemiringan dan kecepatan suatu kurva pada titik tertentu.

Fisika

• Menghitung gaya yang bekerja pada benda bergerak.
• Menentukan kecepatan dan percepatan suatu benda.
• Menganalisis gerak parabola.

Teknik

• Merancang jalan dan rel kereta api dengan kemiringan optimal.
• Menentukan sudut optimum untuk proyektil dan roket.
• Menganalisis tegangan dan regangan pada struktur.

Akhir Kata

Persamaan garis singgung sejajar memainkan peran penting dalam berbagai bidang, termasuk geometri, fisika, dan teknik. Dalam geometri, persamaan ini digunakan untuk menentukan titik potong garis singgung dengan sumbu koordinat, serta untuk menyelesaikan masalah yang melibatkan garis singgung dan lingkaran. Dalam fisika, persamaan garis singgung sejajar digunakan untuk menganalisis lintasan proyektil dan benda yang bergerak melingkar.

Sementara dalam teknik, persamaan ini digunakan untuk merancang jalur pipa, rel kereta api, dan struktur lainnya.

Pertanyaan dan Jawaban

Apa perbedaan antara garis singgung dan garis singgung sejajar?

Garis singgung adalah garis yang menyentuh lingkaran pada satu titik, sedangkan garis singgung sejajar adalah garis singgung yang sejajar dengan garis singgung lainnya pada titik yang berbeda.

Bagaimana cara menentukan persamaan garis singgung sejajar?

Persamaan garis singgung sejajar dapat ditentukan dengan menggunakan persamaan umum garis singgung dan kondisi sejajar dengan garis singgung lainnya.

Apa saja aplikasi garis singgung sejajar?

Garis singgung sejajar memiliki aplikasi dalam berbagai bidang, seperti geometri, fisika, dan teknik, untuk menyelesaikan masalah yang melibatkan garis singgung dan lingkaran.