Dalam dunia matematika, grafik fungsi memainkan peran penting dalam merepresentasikan hubungan antara variabel. Memahami persamaan yang mendasari grafik-grafik ini sangat penting untuk menganalisis dan memecahkan berbagai masalah dalam berbagai bidang.
Artikel ini akan membahas konsep persamaan grafik fungsi, cara menentukannya dari grafik, serta penerapannya dalam kehidupan sehari-hari. Dengan mengeksplorasi topik ini, kita akan mengungkap kekuatan persamaan grafik fungsi dalam memberikan wawasan yang berharga tentang dunia di sekitar kita.
Persamaan Grafik Fungsi
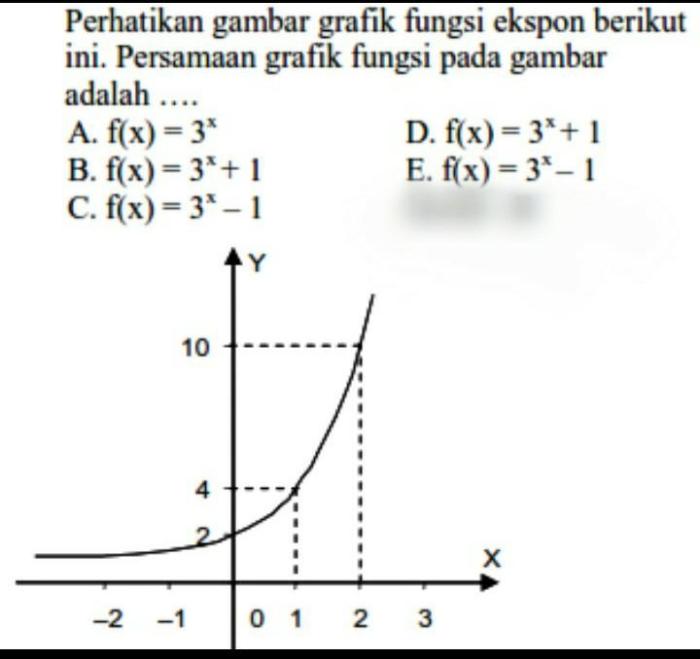
Persamaan grafik fungsi adalah persamaan matematika yang menggambarkan hubungan antara dua variabel, biasanya diwakili oleh x dan y . Grafik fungsi menunjukkan bagaimana nilai y berubah sehubungan dengan nilai x .
Contoh Persamaan Grafik Fungsi Sederhana
Salah satu persamaan grafik fungsi sederhana adalah:
- y = x + 2
Persamaan ini merepresentasikan garis lurus yang memiliki kemiringan 1 dan memotong sumbu y di titik (0, 2).
Perbedaan Persamaan Grafik Fungsi Linear dan Non-Linear
Persamaan grafik fungsi dapat diklasifikasikan menjadi dua jenis utama:
- Linear: Persamaan yang grafiknya berupa garis lurus, seperti y = mx + b.
- Non-linear: Persamaan yang grafiknya bukan garis lurus, seperti y = x2 atau y = sin(x).
Persamaan grafik fungsi linear memiliki kemiringan konstan, sedangkan persamaan grafik fungsi non-linear memiliki kemiringan yang berubah-ubah sehubungan dengan x .
Cara Menentukan Persamaan Grafik Fungsi

Menentukan persamaan grafik fungsi dari grafiknya melibatkan beberapa langkah sistematis yang memungkinkan kita mengekspresikan hubungan matematis antara variabel bebas dan dependen dalam fungsi tersebut.
Langkah-langkah Menentukan Persamaan Grafik Fungsi
- Tentukan Jenis Fungsi: Identifikasi jenis fungsi yang diwakili oleh grafik, seperti linier, kuadrat, atau eksponensial.
- Temukan Titik Penting: Tentukan titik-titik penting pada grafik, seperti titik potong sumbu x dan y, titik maksimum atau minimum, dan titik belok (jika ada).
- Tulis Persamaan Umum: Berdasarkan jenis fungsi yang diidentifikasi, tulis persamaan umum untuk fungsi tersebut. Persamaan ini akan berisi parameter yang tidak diketahui.
- Gunakan Titik-titik Penting: Substitusikan titik-titik penting yang ditemukan pada Langkah 2 ke dalam persamaan umum. Ini akan menghasilkan sistem persamaan yang dapat digunakan untuk menyelesaikan parameter yang tidak diketahui.
- Selesaikan Persamaan: Pecahkan sistem persamaan yang dihasilkan untuk menentukan nilai parameter yang tidak diketahui.
- Tulis Persamaan Akhir: Setelah menyelesaikan parameter, substitusikan nilainya ke dalam persamaan umum untuk mendapatkan persamaan grafik fungsi akhir.
Contoh Langkah demi Langkah
Misalkan kita memiliki grafik fungsi linier yang melewati titik (2, 5) dan (4, 9). Untuk menentukan persamaan grafik fungsi ini, kita dapat mengikuti langkah-langkah berikut:
- Jenis fungsi: Linier
- Titik penting: (2, 5) dan (4, 9)
- Persamaan umum: y = mx + b (persamaan garis lurus)
- Substitusi titik:
- 5 = 2m + b (substitusi titik (2, 5))
- 9 = 4m + b (substitusi titik (4, 9))
- Penyelesaian persamaan:
- b = 1 (diperoleh dari persamaan pertama)
- m = 2 (diperoleh dari persamaan kedua)
- Persamaan akhir: y = 2x + 1
Peran Titik-titik pada Grafik
Titik-titik pada grafik memainkan peran penting dalam menentukan persamaan grafik fungsi. Titik potong sumbu x memberikan informasi tentang titik di mana fungsi berpotongan dengan sumbu x, yang dapat digunakan untuk menemukan akar fungsi. Titik potong sumbu y memberikan informasi tentang nilai fungsi ketika variabel bebas adalah nol.
Titik maksimum dan minimum memberikan informasi tentang nilai ekstrem fungsi, yang dapat digunakan untuk menentukan domain dan jangkauan fungsi. Titik belok memberikan informasi tentang perubahan konveksitas fungsi, yang dapat digunakan untuk menentukan sifat grafik.Dengan menggunakan titik-titik penting ini, kita dapat menentukan persamaan grafik fungsi yang paling sesuai dengan grafik yang diberikan, sehingga memungkinkan kita untuk memodelkan dan memprediksi perilaku fungsi tersebut.
Penerapan Persamaan Grafik Fungsi

Persamaan grafik fungsi memiliki beragam aplikasi dalam berbagai bidang, mulai dari sains dan teknik hingga bisnis dan ekonomi. Memahami persamaan ini sangat penting untuk memecahkan masalah secara efektif dan membuat prediksi berdasarkan data.
Bidang Sains dan Teknik
- Fisika: Persamaan grafik fungsi digunakan untuk menggambarkan gerakan benda, seperti kecepatan dan percepatan.
- Kimia: Persamaan grafik fungsi digunakan untuk menentukan konsentrasi zat dalam reaksi kimia.
- Teknik: Persamaan grafik fungsi digunakan untuk merancang sistem, seperti jembatan dan bangunan, untuk memastikan stabilitas dan efisiensi.
Bidang Bisnis dan Ekonomi
- Analisis Pasar: Persamaan grafik fungsi digunakan untuk memprediksi tren pasar dan permintaan konsumen.
- Manajemen Keuangan: Persamaan grafik fungsi digunakan untuk mengoptimalkan portofolio investasi dan mengelola risiko.
- Pemasaran: Persamaan grafik fungsi digunakan untuk menentukan segmen pasar dan mengembangkan strategi pemasaran yang efektif.
Kehidupan Sehari-hari
Memahami persamaan grafik fungsi juga penting dalam kehidupan sehari-hari. Persamaan ini dapat membantu kita memahami dan memprediksi berbagai fenomena, seperti:
- Pola Cuaca: Persamaan grafik fungsi dapat digunakan untuk memprediksi pola cuaca, seperti suhu dan curah hujan.
- Pergerakan Saham: Persamaan grafik fungsi dapat digunakan untuk melacak pergerakan saham dan membuat keputusan investasi.
- Perencanaan Anggaran: Persamaan grafik fungsi dapat digunakan untuk merencanakan anggaran dan mengelola pengeluaran.
Contoh Soal dan Pembahasan
Menentukan Persamaan Grafik Fungsi
Berikut adalah contoh soal beserta pembahasannya untuk menentukan persamaan grafik fungsi:
- Soal 1: Tentukan persamaan grafik fungsi yang melalui titik (2, 5) dan memiliki gradien 2.
- Pembahasan:
- Persamaan garis lurus dalam bentuk titik-gradien adalah y
– y1 = m(x
– x1), di mana (x1, y1) adalah titik yang dilalui garis dan m adalah gradien garis. - Substitusikan nilai yang diketahui ke dalam persamaan: y
– 5 = 2(x
– 2). - Sederhanakan persamaan: y
– 5 = 2x
– 4. - Persamaan grafik fungsi adalah y = 2x + 1.
- Persamaan garis lurus dalam bentuk titik-gradien adalah y
- Soal 2: Tentukan persamaan grafik fungsi kuadrat yang memiliki titik puncak (3,
-2) dan melalui titik (1, 4). - Pembahasan:
- Persamaan umum fungsi kuadrat adalah y = ax2 + bx + c.
- Substitusikan titik puncak ke dalam persamaan:
-2 = a(3)2 + b(3) + c. - Substitusikan titik lain ke dalam persamaan: 4 = a(1)2 + b(1) + c.
- Selesaikan sistem persamaan untuk mencari nilai a, b, dan c.
- Persamaan grafik fungsi adalah y = x2
– 6x + 11.
Tips dan Trik
Untuk mempermudah penentuan persamaan grafik fungsi, berikut beberapa tips dan trik yang dapat diterapkan:
Teknik Cepat dan Efektif
- Identifikasi Titik Potong Sumbu: Tentukan titik potong fungsi dengan sumbu x dan y untuk mendapatkan gambaran umum grafik.
- Periksa Sifat Grafik: Analisis apakah grafik fungsi genap, ganjil, periodik, atau memiliki simetri tertentu untuk mempersempit persamaan yang mungkin.
- Gunakan Transformasi: Terapkan transformasi seperti pergeseran, peregangan, atau refleksi untuk memodifikasi persamaan dasar dan menghasilkan grafik yang diinginkan.
- Gunakan Kalkulus: Jika memungkinkan, gunakan konsep kalkulus seperti turunan dan integral untuk menentukan sifat grafik, seperti titik balik dan asimtot.
Contoh Penggunaan Tips dan Trik
Misalkan kita ingin menentukan persamaan grafik fungsi yang memotong sumbu x di (2, 0) dan (4, 0), serta memotong sumbu y di (0, 3).
Dengan menggunakan teknik cepat dan efektif di atas, kita dapat menyimpulkan bahwa fungsi tersebut adalah fungsi kuadrat dengan titik balik di (3, 1). Dengan mensubstitusikan titik-titik potong ke dalam persamaan umum fungsi kuadrat, kita memperoleh persamaan:
f(x) = a(x
3)^2 + 1
Untuk menentukan nilai a, kita dapat mensubstitusikan titik (2, 0) ke dalam persamaan tersebut, sehingga:
0 = a(2
3)^2 + 1
a =
1
Dengan demikian, persamaan grafik fungsi yang dimaksud adalah:
f(x) =
- (x
- 3)^2 + 1
Ringkasan Akhir

Persamaan grafik fungsi adalah alat yang ampuh untuk memodelkan dan menganalisis fenomena di berbagai bidang. Dengan memahami cara menentukan dan menerapkan persamaan ini, kita dapat memperoleh pemahaman yang lebih dalam tentang hubungan kompleks yang ada di dunia kita. Kemampuan ini memberdayakan kita untuk membuat prediksi, memecahkan masalah, dan mengambil keputusan yang lebih tepat.
Sudut Pertanyaan Umum (FAQ)
Apa itu persamaan grafik fungsi?
Persamaan grafik fungsi adalah persamaan matematika yang menggambarkan hubungan antara variabel dependen dan independen, yang diwakili sebagai grafik pada bidang koordinat.
Bagaimana cara menentukan persamaan grafik fungsi dari grafik?
Persamaan grafik fungsi dapat ditentukan dengan mengidentifikasi titik-titik kunci pada grafik, seperti titik potong sumbu dan kemiringan garis, dan kemudian menggunakan persamaan yang sesuai untuk merepresentasikan hubungan antara variabel.
Apa saja penerapan persamaan grafik fungsi?
Persamaan grafik fungsi digunakan dalam berbagai bidang, termasuk fisika, ekonomi, dan teknik, untuk memodelkan dan menganalisis berbagai fenomena, seperti gerak benda, pertumbuhan populasi, dan hubungan permintaan dan penawaran.
