Persamaan grafik pada gambar memegang peranan penting dalam berbagai bidang, mulai dari sains hingga bisnis. Dengan merepresentasikan data secara visual, persamaan grafik memungkinkan kita memahami tren, membuat prediksi, dan memperoleh wawasan yang berharga.

Dalam artikel ini, kita akan mengeksplorasi konsep persamaan grafik, cara mengidentifikasi dan menganalisisnya, serta berbagai aplikasinya. Kita juga akan membahas alat dan teknik yang tersedia untuk membantu kita memanfaatkan persamaan grafik secara efektif.

Persamaan Grafik pada Gambar

Persamaan grafik pada gambar adalah representasi matematis dari kurva atau bentuk yang ditampilkan dalam gambar. Persamaan ini memungkinkan kita menentukan sifat dan karakteristik gambar tersebut secara kuantitatif.

Contoh Persamaan Grafik Umum

• Persamaan garis lurus: y = mx + c
• Persamaan lingkaran: (x
  – h)^2 + (y
  – k)^2 = r^2
• Persamaan parabola: y = ax^2 + bx + c
• Persamaan hiperbola: (x
  – h)^2/a^2
  – (y
  – k)^2/b^2 = 1
• Persamaan elips: (x
  – h)^2/a^2 + (y
  – k)^2/b^2 = 1

Pentingnya Memahami Persamaan Grafik

Memahami persamaan grafik sangat penting karena:

• Mengidentifikasi jenis kurva atau bentuk pada gambar.
• Menentukan sifat-sifat gambar, seperti kemiringan, titik potong, dan pusat.
• Memungkinkan manipulasi gambar, seperti pembesaran, rotasi, dan transformasi lainnya.
• Menyederhanakan perhitungan dan analisis gambar.
• Menerapkan persamaan grafik dalam berbagai bidang, seperti fisika, teknik, dan desain grafis.

Cara Mengidentifikasi Persamaan Grafik

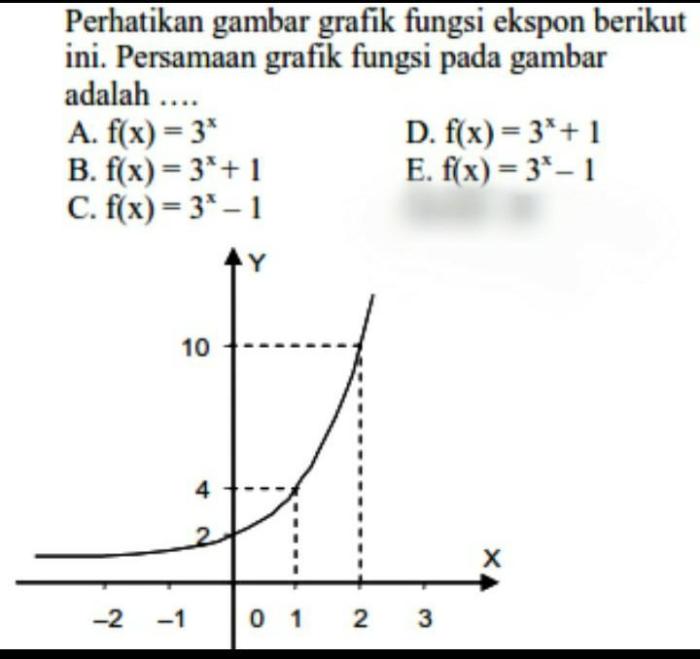
Mengidentifikasi persamaan grafik sangat penting untuk memahami hubungan matematis yang diwakilinya. Berikut adalah langkah-langkah yang dapat diikuti untuk mengidentifikasi persamaan grafik pada gambar:

Menentukan Jenis Grafik

Langkah pertama adalah menentukan jenis grafik yang ditampilkan. Apakah itu garis lurus, parabola, lingkaran, atau bentuk lainnya? Jenis grafik akan memberikan petunjuk tentang persamaan yang sesuai.

Mengidentifikasi Fitur Utama

Setelah jenis grafik diidentifikasi, langkah selanjutnya adalah mengidentifikasi fitur utamanya. Untuk garis lurus, ini termasuk kemiringan dan titik potong y. Untuk parabola, ini termasuk titik puncak dan titik potong x. Untuk lingkaran, ini termasuk pusat dan jari-jari.

Mencocokkan Persamaan

Dengan mengetahui jenis grafik dan fitur utamanya, kita dapat mencocokkan persamaan yang sesuai. Tabel berikut merangkum beberapa jenis grafik umum dan persamaan yang sesuai:

Jenis Grafik	Persamaan
Garis Lurus	y = mx + b
Parabola	y = ax^2 + bx + c
Lingkaran	(x h)^2 + (y k)^2 = r^2

Aplikasi Persamaan Grafik

Persamaan grafik merupakan alat yang ampuh untuk merepresentasikan dan menganalisis hubungan antara variabel. Aplikasi persamaan grafik mencakup berbagai bidang, mulai dari sains hingga bisnis.

Penggunaan dalam Sains

*

-*Fisika

Persamaan grafik digunakan untuk menggambarkan gerak benda, gaya, dan energi. Misalnya, grafik kecepatan-waktu dapat menunjukkan percepatan suatu objek.

• -*Kimia

  Grafik digunakan untuk menganalisis reaksi kimia, seperti konsentrasi reaktan dan produk seiring waktu.

-*Biologi

Persamaan grafik dapat merepresentasikan pertumbuhan populasi, tingkat kematian, dan hubungan antara faktor lingkungan dan kesehatan organisme.

Penggunaan dalam Teknik

*

-*Desain Mesin

Grafik digunakan untuk menganalisis tegangan dan regangan pada struktur, seperti jembatan dan pesawat terbang.

• -*Elektronika

  Grafik membantu dalam desain dan analisis rangkaian listrik, seperti impedansi dan respons frekuensi.

-*Ilmu Komputer

Persamaan grafik digunakan dalam visualisasi data, pemrosesan gambar, dan simulasi.

Penggunaan dalam Bisnis

*

-*Analisis Pasar

Grafik dapat menggambarkan tren penjualan, pangsa pasar, dan perilaku konsumen.

• -*Perencanaan Keuangan

  Persamaan grafik membantu dalam memprediksi arus kas, profitabilitas, dan pengembalian investasi.

-*Manajemen Operasi

Grafik digunakan untuk mengoptimalkan proses produksi, mengelola inventaris, dan menjadwalkan sumber daya.

Keterbatasan dan Pertimbangan

Meskipun persamaan grafik sangat berguna, namun terdapat keterbatasan dan pertimbangan yang perlu diperhatikan:*

-*Kompleksitas

Grafik yang mewakili hubungan yang kompleks dapat sulit diinterpretasikan.

• -*Data yang Tidak Akurat

  Jika data yang digunakan untuk membuat grafik tidak akurat, hasilnya juga akan tidak akurat.

-*Tidak Berlaku untuk Semua Kasus

Persamaan grafik mungkin tidak berlaku untuk semua situasi atau kondisi.

-*Pertimbangan Skala

Penting untuk mempertimbangkan skala grafik untuk memastikan interpretasi yang benar.

Alat dan Teknik untuk Menganalisis Persamaan Grafik

Analisis persamaan grafik sangat penting dalam matematika dan sains. Berbagai alat dan teknik dapat membantu memvisualisasikan, memanipulasi, dan menganalisis grafik ini.

Perangkat Lunak Analisis Grafik

• GeoGebra: Perangkat lunak gratis dan sumber terbuka untuk membuat dan menganalisis grafik interaktif.
• Desmos: Platform online yang menyediakan alat pembuatan grafik dan analisis yang komprehensif.
• MATLAB: Lingkungan pemrograman teknis yang mencakup fitur ekstensif untuk analisis dan visualisasi grafik.

Metode Analisis

• Intersepsi: Menemukan titik-titik di mana grafik memotong sumbu x dan y.
• Kemiringan: Mengukur kemiringan garis atau kurva, memberikan informasi tentang perubahan variabel.
• Ekstrem: Mengidentifikasi titik maksimum dan minimum grafik, menunjukkan nilai maksimum dan minimum fungsi.
• Asimptot: Menemukan garis lurus yang didekati grafik saat x atau y mendekati tak terhingga.

Alur Kerja Analisis Persamaan Grafik

• Plot grafik: Menggunakan perangkat lunak atau metode manual untuk membuat representasi visual persamaan.
• Tentukan fitur utama: Mengidentifikasi intersepsi, kemiringan, ekstrem, dan asimptot.
• Analisis hubungan: Menafsirkan hubungan antara variabel yang direpresentasikan oleh grafik.
• Membuat prediksi: Menggunakan analisis grafik untuk membuat prediksi atau estimasi tentang perilaku fungsi.

Sumber Daya untuk Mempelajari Persamaan Grafik

Mempelajari persamaan grafik sangat penting untuk memahami hubungan antara variabel aljabar dan representasi grafisnya. Berikut adalah beberapa sumber daya yang dapat membantu Anda mempelajari topik ini lebih dalam:

Buku Teks

• Prekalkulus: Persamaan dan Fungsi oleh Stewart, Redlin, dan Watson
• Algebra and Trigonometry oleh Sullivan dan Sullivan
• College Algebra oleh Aufmann, Barker, dan Lockwood

Kursus Online

• Persamaan Grafik di Coursera
• Persamaan Grafik untuk Pemula di Udemy
• Kursus Persamaan Grafik di Khan Academy

Tutorial Video

• Persamaan Grafik oleh PatrickJMT
• Memahami Persamaan Grafik oleh Khan Academy
• Cara Menggambar Persamaan Grafik oleh Math Antics

Komunitas dan Forum

Terhubung dengan komunitas dan forum online dapat memberikan dukungan dan kesempatan untuk bertukar pengetahuan tentang persamaan grafik:

• Forum Persamaan Grafik di Math Stack Exchange
• Grup Facebook Persamaan Grafik untuk Siswa
• Komunitas Reddit Persamaan Grafik

Simpulan Akhir

Memahami persamaan grafik adalah keterampilan penting yang membuka pintu menuju pemahaman dan pemecahan masalah yang lebih mendalam. Dengan menguasai konsep ini, kita dapat memanfaatkan kekuatan representasi visual untuk memperoleh wawasan yang berharga dan membuat keputusan yang lebih tepat.

Pertanyaan Umum (FAQ)

Apa itu persamaan grafik?

Persamaan grafik adalah representasi visual dari hubungan matematis antara dua atau lebih variabel, yang diplot pada sistem koordinat.

Bagaimana cara mengidentifikasi persamaan grafik?

Identifikasi persamaan grafik melibatkan analisis fitur-fitur utama grafik, seperti titik potong, kemiringan, dan bentuk umum.

Apa saja aplikasi persamaan grafik?

Persamaan grafik digunakan dalam berbagai bidang, seperti sains, teknik, dan bisnis, untuk memahami tren, membuat prediksi, dan memecahkan masalah.

Apa saja alat dan teknik untuk menganalisis persamaan grafik?

Alat dan teknik untuk menganalisis persamaan grafik meliputi perangkat lunak pemetaan, metode aljabar, dan teknik kalkulus.