Dalam ranah geometri, persamaan lingkaran menyinggung garis memegang peran penting dalam mengungkap sifat-sifat unik dan aplikasi praktis dari bentuk-bentuk geometris. Lingkaran menyinggung garis adalah suatu lingkaran yang memiliki satu titik singgung dengan sebuah garis lurus. Pemahaman tentang persamaan yang mendasari bentuk geometris ini sangat penting untuk berbagai bidang, termasuk matematika, fisika, dan teknik.
Persamaan lingkaran menyinggung garis memberikan wawasan tentang hubungan antara dua entitas geometris ini, memungkinkan kita menentukan sifat-sifat penting seperti jari-jari lingkaran, jarak dari pusat lingkaran ke garis, dan koordinat titik singgung. Dengan memahami persamaan ini, kita dapat memecahkan masalah geometris yang kompleks dan menerapkan pengetahuan kita pada aplikasi dunia nyata.
Persamaan Lingkaran Menyinggung Garis
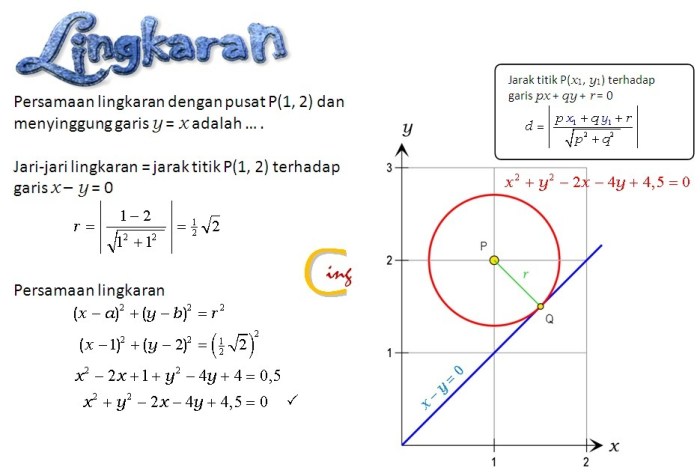
Lingkaran menyinggung garis adalah lingkaran yang memiliki satu titik singgung dengan garis tersebut. Titik singgung adalah titik di mana lingkaran dan garis saling bersentuhan tanpa saling memotong.
Rumus Umum Persamaan Lingkaran Menyinggung Garis
Persamaan umum lingkaran menyinggung garis adalah:
$$(x
- h)^2 + (y
- k)^2 = r^2$$
di mana:* (h, k) adalah koordinat pusat lingkaran
- r adalah jari-jari lingkaran
- Garis memiliki persamaan y = mx + c
Cara Mencari Persamaan Lingkaran Menyinggung Garis
Menentukan persamaan lingkaran yang menyinggung garis merupakan langkah penting dalam berbagai aplikasi geometri dan aljabar. Berikut adalah langkah-langkah untuk menentukan persamaan lingkaran tersebut:
Menentukan Persamaan Garis
Tentukan persamaan garis yang bersinggungan dengan lingkaran. Persamaan garis dapat dinyatakan dalam bentuk y = mx + c, di mana m adalah gradien dan c adalah konstanta.
Menentukan Jarak dari Pusat ke Garis
Hitung jarak dari pusat lingkaran ke garis. Jarak ini sama dengan jari-jari lingkaran dan dapat dihitung menggunakan rumus berikut:
r = |(y2
- y1)
- m(x2
- x1)| / √(1 + m²)
di mana (x1, y1) dan (x2, y2) adalah dua titik pada garis.
Menentukan Persamaan Lingkaran
Tentukan persamaan lingkaran menggunakan rumus persamaan lingkaran:
(x
- h)² + (y
- k)² = r²
di mana (h, k) adalah koordinat pusat lingkaran dan r adalah jari-jarinya.
Contoh Soal
Tentukan persamaan lingkaran yang menyinggung garis y = 2x + 1 dan berpusat di titik (2, -1).
Solusi:
1.
-*Menentukan Jarak dari Pusat ke Garis
- r = |(2
- (-1))
- 2(0
- 2)| / √(1 + 2²) = 5
- 2.
-*Menentukan Persamaan Lingkaran
- (x
- 2)² + (y + 1)² = 5²
-
-*Persamaan Lingkaran
(x
- 2)² + (y + 1)² = 25
Sifat-Sifat Lingkaran Menyinggung Garis

Lingkaran yang menyinggung garis memiliki sifat-sifat khusus yang membedakannya dari lingkaran lainnya. Sifat-sifat ini berkaitan dengan panjang jari-jari lingkaran dan jarak dari pusat lingkaran ke garis.
Jarak dari Pusat Lingkaran ke Garis
Jarak dari pusat lingkaran ke garis singgung sama dengan jari-jari lingkaran.
Panjang Jari-jari Lingkaran
Panjang jari-jari lingkaran yang menyinggung garis dapat dihitung menggunakan rumus berikut:
r = d/2
di mana:
- r adalah jari-jari lingkaran
- d adalah jarak dari pusat lingkaran ke garis
Tabel Sifat-Sifat Lingkaran Menyinggung Garis
Sifat-sifat lingkaran menyinggung garis dapat dirangkum dalam tabel berikut:
| Sifat | Rumus |
|---|---|
| Jarak dari pusat lingkaran ke garis | d = r |
| Panjang jari-jari lingkaran | r = d/2 |
Penerapan Persamaan Lingkaran Menyinggung Garis

Persamaan lingkaran menyinggung garis memiliki banyak penerapan dalam kehidupan nyata, terutama dalam bidang arsitektur dan desain.
Penerapan dalam Arsitektur
- Membuat Lengkungan dan Kubah: Persamaan lingkaran menyinggung garis digunakan untuk menentukan bentuk lengkungan dan kubah pada bangunan, memastikan kelancaran dan estetika.
- Desain Jendela dan Pintu: Lingkaran menyinggung garis dapat digunakan untuk mendesain bentuk jendela dan pintu yang melengkung, memberikan sentuhan dekoratif pada bangunan.
Penerapan dalam Desain
- Desain Produk: Persamaan ini diterapkan dalam desain produk untuk membuat bentuk melengkung yang estetis dan fungsional, seperti pada kursi, lampu, dan vas.
li> Desain Grafis: Lingkaran menyinggung garis digunakan dalam desain grafis untuk membuat logo, ikon, dan elemen dekoratif lainnya yang berkesan dan menarik secara visual.
Kesulitan dan Trik
Mencari persamaan lingkaran menyinggung garis dapat menimbulkan beberapa kesulitan.
Berikut adalah beberapa tips dan trik untuk mengatasinya:
Identifikasi Kesulitan
- Menentukan titik pusat dan jari-jari lingkaran yang memenuhi persyaratan.
- Memastikan lingkaran menyinggung garis pada titik tertentu.
- Menyelesaikan persamaan kuadrat yang dihasilkan dari proses penyinggungan.
Trik Mengatasi
- Gunakan persamaan garis dan lingkaran untuk membentuk sistem persamaan.
- Gunakan rumus jarak dari titik ke garis untuk memastikan penyinggungan.
- Faktorkan persamaan kuadrat untuk menemukan solusi nyata.
- Perhatikan bahwa mungkin ada dua solusi, satu untuk setiap titik singgung.
Kesimpulan Akhir

Persamaan lingkaran menyinggung garis adalah alat yang ampuh untuk mengungkap sifat-sifat geometris yang menarik dan memiliki aplikasi praktis yang luas. Dengan menguasai persamaan ini, kita dapat memperoleh pemahaman yang lebih dalam tentang hubungan antara lingkaran dan garis, memecahkan masalah geometris yang menantang, dan memanfaatkan pengetahuan kita untuk memecahkan masalah dunia nyata di berbagai bidang.
Pertanyaan Umum (FAQ)
Apa pentingnya persamaan lingkaran menyinggung garis?
Persamaan ini sangat penting karena memungkinkan kita menentukan sifat-sifat geometris dari lingkaran menyinggung garis, seperti jari-jari, titik singgung, dan jarak dari pusat lingkaran ke garis.
Bagaimana cara menggunakan persamaan lingkaran menyinggung garis?
Persamaan ini dapat digunakan untuk memecahkan berbagai masalah geometris, seperti menentukan persamaan lingkaran yang menyinggung garis tertentu atau menentukan titik singgung antara lingkaran dan garis.
Di bidang apa saja persamaan lingkaran menyinggung garis diterapkan?
Persamaan ini diterapkan di berbagai bidang, termasuk matematika, fisika, teknik, dan arsitektur.
