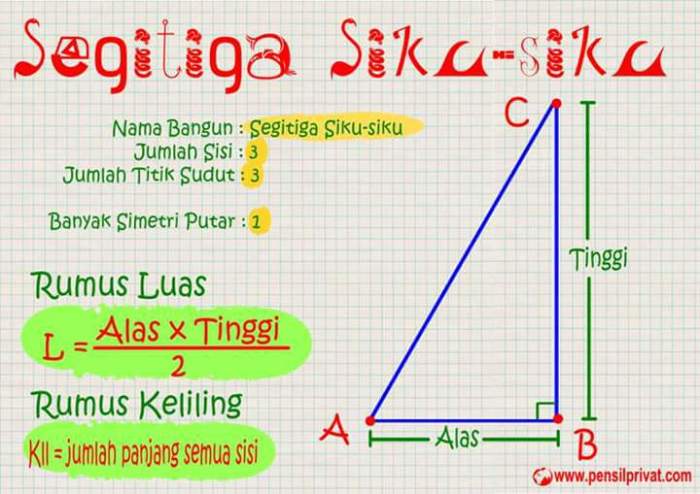
Dalam geometri, segitiga siku-siku memainkan peran penting dalam memahami hubungan antara sisi dan sudut. Rumus kesebangunan segitiga siku-siku menjadi alat yang sangat berharga dalam mengungkap hubungan ini, memungkinkan kita untuk memecahkan masalah dan memperoleh wawasan yang berharga tentang bentuk geometris dasar ini.
Rumus-rumus ini tidak hanya terbatas pada ranah akademis, tetapi juga memiliki aplikasi luas dalam bidang teknik, arsitektur, dan desain, di mana pemahaman tentang hubungan sisi dan sudut segitiga siku-siku sangat penting untuk memastikan stabilitas, efisiensi, dan estetika.
Rumus Kesebangunan Segitiga Siku-Siku
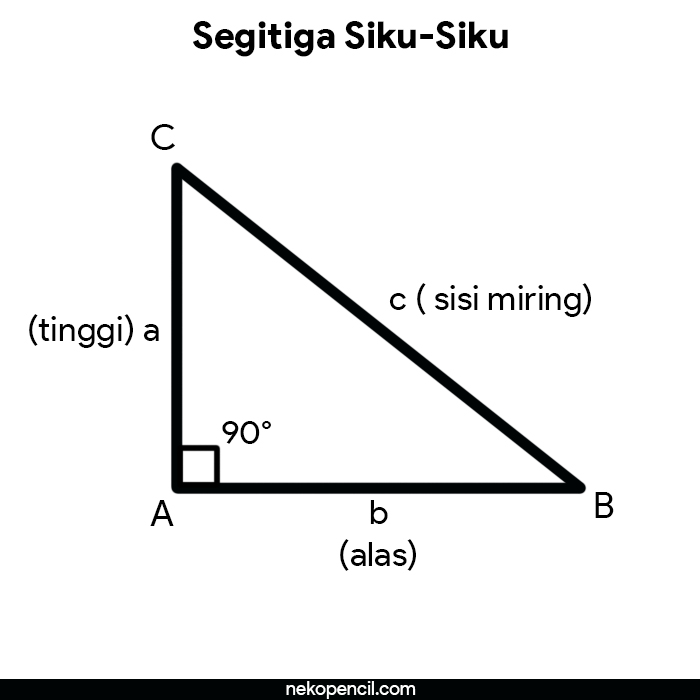
Segitiga siku-siku yang memiliki panjang sisi sebanding disebut segitiga siku-siku sebangun. Dalam segitiga siku-siku sebangun, berlaku rumus-rumus tertentu yang menghubungkan panjang sisi-sisinya.
Rumus Kesebangunan Segitiga Siku-Siku
Jika segitiga siku-siku ABC dan DEF sebangun, maka berlaku rumus-rumus berikut:
- AB/DE = BC/EF = AC/DF
- AB2/DE2 = BC2/EF2 = AC2/DF2
- AB2 + BC2 = AC2
- DE2 + EF2 = DF2
Contoh Penerapan Rumus Kesebangunan Segitiga Siku-Siku
Diketahui segitiga siku-siku ABC dan DEF sebangun dengan AB = 6 cm, BC = 8 cm, DE = 4 cm, dan EF = 6 cm. Hitunglah panjang DF.
Menggunakan rumus kesebangunan, kita dapat menghitung DF sebagai berikut:
AB/DE = AC/DF
6/4 = AC/DF
AC = (6/4)DF = 1,5DF
Menggunakan teorema Pythagoras pada segitiga ABC, kita dapat mencari panjang AC:
AC 2 = AB 2 + BC 2
(1,5DF) 2 = 6 2 + 8 2
2,25DF 2 = 100
DF 2 = 44,44
DF = √44,44 = 6,67 cm
Jadi, panjang DF adalah 6,67 cm.
Sifat-Sifat Segitiga Siku-Siku
Segitiga siku-siku memiliki beberapa sifat khusus yang terkait dengan kesebangunannya.
Salah satu sifat penting adalah jika dua segitiga siku-siku memiliki sisi miring yang sebanding, maka segitiga tersebut sebangun.
Sifat-Sifat Kesebangunan Segitiga Siku-Siku
- Jika dua segitiga siku-siku memiliki sisi miring yang sebanding, maka segitiga tersebut sebangun.
- Jika dua segitiga siku-siku memiliki dua sisi siku-siku yang sebanding, maka segitiga tersebut sebangun.
- Jika dua segitiga siku-siku memiliki satu sisi siku-siku dan sisi miring yang sebanding, maka segitiga tersebut sebangun.
Sifat-sifat ini dapat dibuktikan menggunakan teorema Pythagoras dan kesebangunan segitiga.
Aplikasi Rumus Kesebangunan dalam Kehidupan Nyata
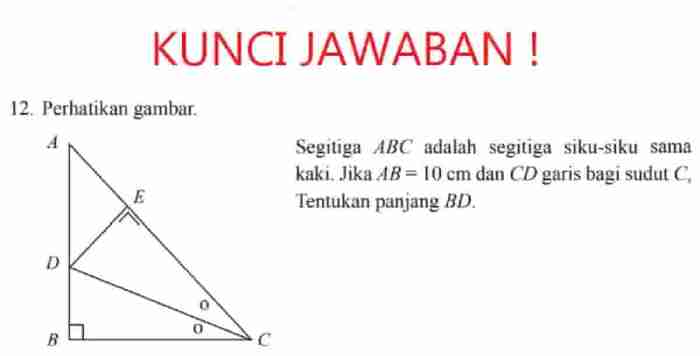
Rumus kesebangunan segitiga siku-siku memiliki berbagai aplikasi praktis dalam bidang teknik, arsitektur, dan desain. Rumus ini membantu menyelesaikan masalah yang melibatkan pengukuran dan perbandingan segitiga siku-siku yang sebangun.
Bidang Teknik
- Perancangan Struktur: Rumus kesebangunan digunakan untuk menentukan beban dan tekanan pada struktur, seperti jembatan dan gedung. Dengan mengetahui perbandingan ukuran dan sudut segitiga siku-siku yang terlibat, insinyur dapat memprediksi kekuatan dan stabilitas struktur.
- Konstruksi Mesin: Dalam perancangan mesin, rumus kesebangunan digunakan untuk menghitung ukuran dan rasio roda gigi, poros, dan komponen lainnya. Dengan menjaga kesebangunan, insinyur dapat memastikan kinerja mesin yang efisien dan optimal.
Bidang Arsitektur
- Perancangan Bangunan: Arsitek menggunakan rumus kesebangunan untuk menentukan tinggi bangunan, ukuran jendela, dan proporsi ruangan. Dengan mempertahankan kesebangunan, mereka dapat menciptakan bangunan yang estetis dan fungsional.
- Pembangunan Lansekap: Dalam desain lansekap, rumus kesebangunan digunakan untuk merencanakan jalur, taman bunga, dan fitur lanskap lainnya. Ini membantu menciptakan ruang luar yang seimbang dan harmonis.
Bidang Desain
- Desain Grafis: Desainer grafis menggunakan rumus kesebangunan untuk memastikan proporsi yang tepat dalam logo, poster, dan desain lainnya. Ini membantu menciptakan desain yang estetis dan menarik secara visual.
- Desain Produk: Dalam desain produk, rumus kesebangunan digunakan untuk menentukan ukuran dan bentuk komponen produk, seperti furnitur, peralatan, dan kendaraan. Dengan menjaga kesebangunan, desainer dapat menciptakan produk yang fungsional dan menarik.
Cara Menggunakan Rumus Kesebangunan
Rumus kesebangunan segitiga siku-siku dapat digunakan untuk menentukan panjang sisi yang tidak diketahui dalam segitiga siku-siku berdasarkan panjang sisi yang diketahui. Berikut langkah-langkah terperinci untuk menggunakan rumus ini:
- Tentukan sisi yang diketahui dan tidak diketahui. Identifikasi sisi yang panjangnya diketahui dan sisi yang panjangnya tidak diketahui.
- Pilih rumus yang sesuai. Tergantung pada sisi yang diketahui dan tidak diketahui, pilih salah satu rumus berikut:
- Sisi yang berhadapan dengan sudut 30°: a = b/√2
- Sisi yang berhadapan dengan sudut 45°: a = b/√2
- Sisi yang berhadapan dengan sudut 60°: a = b/2
- Substitusikan nilai yang diketahui. Masukkan nilai sisi yang diketahui ke dalam rumus yang dipilih.
- Selesaikan persamaan. Hitung panjang sisi yang tidak diketahui dengan menyelesaikan persamaan yang dihasilkan.
| Rumus | Sisi yang Diketahui | Sisi yang Tidak Diketahui |
|---|---|---|
| a = b/√2 | Sisi yang berhadapan dengan sudut 30° atau 45° | Sisi yang berhadapan dengan sudut 60° atau 90° |
| a = b/2 | Sisi yang berhadapan dengan sudut 60° | Sisi yang berhadapan dengan sudut 30° atau 90° |
Kesalahan Umum dan Cara Menghindarinya

Meskipun rumus kesebangunan segitiga siku-siku relatif sederhana, ada beberapa kesalahan umum yang dapat dilakukan. Kesalahan ini dapat menyebabkan jawaban yang salah atau membingungkan.
Untuk menghindari kesalahan-kesalahan ini, penting untuk memahami rumus dan penerapannya dengan benar. Berikut adalah beberapa kesalahan umum yang perlu diperhatikan dan cara menghindarinya:
Menggunakan Rumus yang Salah
- Hindari menggunakan rumus kesebangunan yang salah. Ada tiga rumus kesebangunan utama untuk segitiga siku-siku, dan penting untuk memilih rumus yang sesuai dengan informasi yang diberikan.
Menggunakan Unit yang Berbeda
- Pastikan untuk menggunakan unit yang sama untuk semua pengukuran. Misalnya, jika panjang sisi miring diberikan dalam sentimeter, maka panjang sisi lainnya juga harus dikonversi ke sentimeter sebelum menggunakan rumus.
Membulatkan Terlalu Dini
- Hindari membulatkan hasil terlalu dini. Meskipun mungkin tergoda untuk membulatkan jawaban ke bilangan bulat terdekat, hal ini dapat menyebabkan kesalahan yang signifikan, terutama untuk pengukuran yang sangat kecil atau besar.
Mengabaikan Tanda Negatif
- Perhatikan tanda negatif pada rumus kesebangunan. Tanda negatif ini menunjukkan bahwa sisi yang berlawanan dengan sudut lancip tertentu akan memiliki panjang negatif. Jangan abaikan tanda negatif ini, karena dapat menyebabkan kesalahan dalam perhitungan.
Mencampur Sudut dan Sisi
- Hindari mencampur sudut dan sisi saat menggunakan rumus kesebangunan. Rumus ini hanya berlaku untuk segitiga siku-siku, yang memiliki sudut siku-siku (90 derajat). Pastikan untuk mengidentifikasi sudut siku-siku dengan benar sebelum menggunakan rumus.
Penutup

Dengan memahami rumus kesebangunan segitiga siku-siku dan sifat-sifat yang terkait, kita memperoleh alat yang ampuh untuk memecahkan masalah, merancang struktur, dan memahami dunia di sekitar kita. Rumus-rumus ini menjadi dasar bagi banyak konsep geometris yang lebih kompleks, sehingga menjadikannya landasan yang tak ternilai dalam perjalanan kita untuk mengungkap misteri dunia geometris.
Pertanyaan Umum yang Sering Muncul
Apakah rumus kesebangunan segitiga siku-siku hanya berlaku untuk segitiga siku-siku?
Tidak, rumus kesebangunan juga dapat diterapkan pada segitiga yang sebangun dengan segitiga siku-siku.
Bagaimana cara menggunakan rumus kesebangunan untuk mencari panjang sisi yang hilang?
Gunakan perbandingan sisi yang sesuai untuk membuat persamaan dan selesaikan untuk sisi yang tidak diketahui.
Apa saja aplikasi praktis rumus kesebangunan dalam kehidupan nyata?
Dalam teknik, arsitektur, dan desain, rumus kesebangunan digunakan untuk menentukan ukuran dan proporsi struktur, memastikan stabilitas dan efisiensi.