Dalam matematika dan fisika, perkalian skalar dua vektor merupakan operasi aljabar yang menghasilkan besaran skalar. Berbeda dengan perkalian vektor yang menghasilkan vektor baru, perkalian skalar memberikan informasi tentang besar dan arah relatif dua vektor yang terlibat. Pemahaman mendalam tentang rumus perkalian skalar sangat penting untuk berbagai aplikasi di berbagai bidang, mulai dari fisika hingga teknik.
Konsep perkalian skalar ini akan dibahas secara mendalam dalam artikel ini, meliputi rumus, sifat, aplikasi, serta contoh dan prosedur perhitungannya. Dengan memahami dasar-dasar ini, pembaca akan dapat menerapkan rumus perkalian skalar secara efektif dalam berbagai konteks.
Definisi Perkalian Skalar Dua Vektor
Perkalian skalar, tidak seperti perkalian vektor, menghasilkan skalar (bilangan) yang mewakili besaran dari suatu besaran fisika yang dinyatakan dalam bentuk vektor. Hasil perkalian skalar dua vektor tidak bergantung pada arah kedua vektor tersebut, melainkan hanya pada besarnya dan sudut yang terbentuk di antara keduanya.
Secara matematis, perkalian skalar dua vektor a dan b ditulis sebagai:
a • b = | a | | b | cos θ
di mana:
- |a| dan |b| adalah besar vektor a dan b, masing-masing.
- θ adalah sudut antara vektor a dan b.
Sebagai contoh, misalkan kita memiliki dua vektor a = (2, 3) dan b = (4, 1). Hasil perkalian skalar kedua vektor tersebut adalah:
a • b = (2, 3) • (4, 1) = 2(4) + 3(1) = 11
Rumus Perkalian Skalar
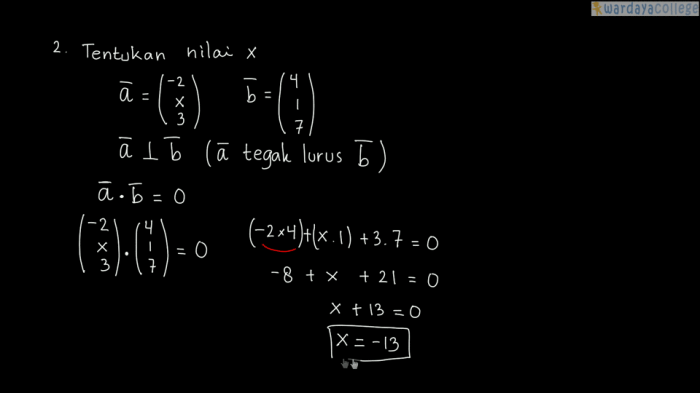
Perkalian skalar adalah operasi matematika yang menghasilkan nilai skalar dari dua vektor. Ini berbeda dari perkalian vektor, yang menghasilkan vektor baru.
Rumus perkalian skalar dua vektor a dan b adalah:
a · b = |a| |b| cos θ
di mana:
- a · b adalah hasil perkalian skalar
- |a| dan |b| adalah besaran vektor a dan b
- θ adalah sudut antara vektor a dan b
Bukti:
Misalkan a = (a 1 , a 2 , a 3 ) dan b = (b 1 , b 2 , b 3 ) adalah dua vektor dalam ruang tiga dimensi.
Maka hasil perkalian skalarnya adalah:
a · b = a 1 b 1 + a 2 b 2 + a 3 b 3
Besaran vektor a dan b diberikan oleh:
|a| = √(a 1 2 + a 2 2 + a 3 2 )
|b| = √(b 1 2 + b 2 2 + b 3 2 )
Sudut antara vektor a dan b diberikan oleh:
cos θ = (a 1 b 1 + a 2 b 2 + a 3 b 3 ) / (|a| |b|)
Dengan mensubstitusikan persamaan ini ke dalam rumus perkalian skalar, kita memperoleh:
a · b = |a| |b| cos θ
Sifat Perkalian Skalar
Perkalian skalar memiliki sifat-sifat tertentu yang mendefinisikan perilakunya. Sifat-sifat ini meliputi komutatif, distributif, dan asosiatif.
Sifat Komutatif
Sifat komutatif menyatakan bahwa mengubah urutan vektor dalam perkalian skalar tidak memengaruhi hasilnya. Secara matematis, untuk vektor a dan b, berlaku:
a ⋅ b = b ⋅ a
Contoh: Jika a = (2, 3) dan b = (4, 5), maka:
a ⋅ b = (2)(4) + (3)(5) = 23b ⋅ a = (4)(2) + (5)(3) = 23
Sifat Distributif
Sifat distributif menyatakan bahwa perkalian skalar dapat didistribusikan ke penjumlahan vektor. Untuk vektor a, b, dan c, berlaku:
a ⋅ (b + c) = a ⋅ b + a ⋅ c
Contoh: Jika a = (2, 1), b = (3, 4), dan c = (5, 6), maka:
a ⋅ (b + c) = (2)(3 + 5) + (1)(4 + 6) = 26a ⋅ b + a ⋅ c = (2)(3) + (2)(5) + (1)(4) + (1)(6) = 26
Sifat Asosiatif
Sifat asosiatif menyatakan bahwa pengelompokan vektor dalam perkalian skalar tidak memengaruhi hasilnya. Untuk vektor a, b, dan c, berlaku:
(a ⋅ b) ⋅ c = a ⋅ (b ⋅ c)
Contoh: Jika a = (1, 2), b = (3, 4), dan c = (5, 6), maka:
(a ⋅ b) ⋅ c = ((1)(3) + (2)(4)) ⋅ (5) = 23a ⋅ (b ⋅ c) = (1) ⋅ ((3)(5) + (4)(6)) = 23
Aplikasi Perkalian Skalar

Perkalian skalar memiliki berbagai aplikasi dalam berbagai bidang, termasuk fisika, teknik, dan matematika. Ini digunakan untuk menghitung besaran seperti kerja, energi, dan proyeksi vektor.
Fisika
- Kerja: Perkalian skalar digunakan untuk menghitung kerja yang dilakukan oleh gaya pada suatu benda. Kerja adalah besaran skalar yang didefinisikan sebagai perkalian skalar antara gaya dan perpindahan.
- Energi: Perkalian skalar juga digunakan untuk menghitung energi potensial dan kinetik. Energi potensial adalah besaran skalar yang didefinisikan sebagai perkalian skalar antara gaya dan perpindahan, sedangkan energi kinetik adalah besaran skalar yang didefinisikan sebagai perkalian skalar antara massa dan kuadrat kecepatan.
Teknik
- Proyeksi Vektor: Perkalian skalar digunakan untuk menghitung proyeksi suatu vektor pada vektor lainnya. Proyeksi vektor adalah besaran skalar yang didefinisikan sebagai perkalian skalar antara vektor yang diproyeksikan dan vektor yang menjadi acuan proyeksi.
- Sudut antara Dua Vektor: Perkalian skalar dapat digunakan untuk menghitung sudut antara dua vektor. Sudut antara dua vektor adalah besaran skalar yang didefinisikan sebagai kosinus invers dari hasil bagi perkalian skalar kedua vektor dengan hasil kali besar kedua vektor.
Matematika
- Orthogonalitas: Perkalian skalar dapat digunakan untuk menentukan apakah dua vektor ortogonal atau tidak. Dua vektor dikatakan ortogonal jika perkalian skalarnya sama dengan nol.
- Pembuktian Identitas: Perkalian skalar dapat digunakan untuk membuktikan berbagai identitas trigonometri dan aljabar.
Contoh dan Prosedur
Perkalian skalar dua vektor dapat digunakan untuk menyelesaikan berbagai masalah fisika dan teknik. Berikut adalah langkah-langkah untuk menghitung perkalian skalar:
Langkah-langkah Perkalian Skalar
- Tentukan dua vektor, a dan b.
- Hitung besar vektor a dan b menggunakan rumus:
- |a| = √(ax2 + ay2 + az2)
- |b| = √(bx2 + by2 + bz2)
- Hitung sudut antara vektor a dan b menggunakan rumus:
- cos θ = (axbx + ayby + azbz) / (|a||b|)
- Hitung perkalian skalar menggunakan rumus:
- a · b = |a||b|cos θ
Contoh Soal
Soal:Hitunglah perkalian skalar dari dua vektor berikut: a = 3i + 4j
5k
b = 2i
j + 3k
Jawab:
1. Hitung besar vektor
|a| = √(3 2 + 4 2 + (-5) 2 ) = √50 |b| = √(2 2 + (-1) 2 + 3 2 ) = √14
2. Hitung sudut antara vektor
cos θ = (3×2 + 4×(-1) + (-5)×3) / (√50×√14) =
1/5
θ = arccos(-1/5) = 108,43°
3. Hitung perkalian skalar
a · b = √50×√14×(-1/5) =
14
Tabel Ringkasan

Tabel berikut merangkum rumus perkalian skalar, sifat-sifatnya, dan aplikasinya.
Setiap entri menyertakan kolom untuk contoh dan penjelasan singkat.
Rumus Perkalian Skalar
- Rumus: • $a \cdot b = |a| |b| \cos \theta$
- Sifat: • Hasil perkalian skalar adalah skalar.
- Contoh: • Jika $a = (3, 4)$ dan $b = (5,
-2)$, maka $a \cdot b = (3)(5) + (4)(-2) = 11$. - Penjelasan: • Rumus ini menghitung hasil perkalian skalar dua vektor dengan mengalikan besar kedua vektor dan kosinus sudut di antara mereka.
Sifat-Sifat Perkalian Skalar
- Komutatif: • $a \cdot b = b \cdot a$
- Distributif: • $a \cdot (b + c) = a \cdot b + a \cdot c$
- Skalar Distributif: • $k(a \cdot b) = (ka) \cdot b = a \cdot (kb)$
- Nilai Nol: • $a \cdot 0 = 0$
- Nilai Identitas: • $a \cdot a = |a|^2$
Aplikasi Perkalian Skalar
- Menghitung Sudut: • $\cos \theta = \fraca \cdot b|a| |b|$
- Menghitung Proyeksi: • Proyeksi vektor $a$ ke arah vektor $b$ adalah $a \cdot \fracb|b|$
- Menghitung Kerja: • Kerja yang dilakukan oleh gaya $F$ pada perpindahan $d$ adalah $W = F \cdot d$
Ilustrasi Grafis

Konsep Geometris
Perkalian skalar dua vektor dapat divisualisasikan secara geometris sebagai berikut:
- Dua vektor, a dan b, direpresentasikan sebagai garis berarah yang berasal dari titik yang sama.
- Sudut θ antara dua vektor diukur berlawanan arah jarum jam dari a ke b.
- Panjang vektor a dilambangkan sebagai ‖a‖, dan panjang vektor b dilambangkan sebagai ‖b‖.
Rumus Perkalian Skalar
Perkalian skalar dua vektor a dan b , dinotasikan sebagai a ⋅ b , dihitung sebagai:
a ⋅ b = ‖ a ‖‖ b ‖cosθ
di mana θ adalah sudut antara dua vektor.
Penutupan
Rumus perkalian skalar dua vektor merupakan alat yang ampuh dalam matematika dan fisika, memungkinkan kita untuk menghitung besaran skalar yang penting seperti kerja, energi, dan proyeksi vektor. Dengan memahami rumus, sifat, dan aplikasinya, kita dapat memanfaatkan perkalian skalar untuk memecahkan masalah dan memperoleh wawasan berharga tentang perilaku vektor dalam berbagai situasi.
Ringkasan FAQ
Apa perbedaan antara perkalian skalar dan perkalian vektor?
Perkalian skalar menghasilkan besaran skalar, sedangkan perkalian vektor menghasilkan vektor baru.
Bagaimana cara menghitung perkalian skalar dua vektor?
Gunakan rumus perkalian skalar: a · b = |a| |b| cos θ, di mana a dan b adalah vektor, |a| dan |b| adalah besarnya, dan θ adalah sudut di antara mereka.
Apa saja sifat perkalian skalar?
Komutatif, distributif, dan asosiatif.
Apa saja aplikasi perkalian skalar?
Menghitung kerja, energi, proyeksi vektor, dan besaran skalar lainnya.
