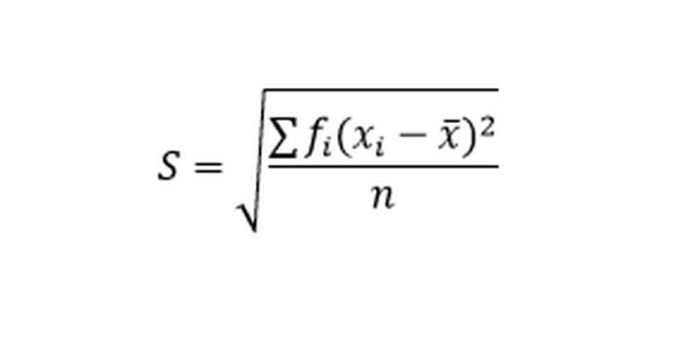Ragam data kelompok merupakan ukuran variabilitas dalam suatu kumpulan data, yang memberikan wawasan tentang penyebaran data di sekitar nilai rata-rata. Memahami rumus ragam data kelompok sangat penting untuk analisis data yang akurat dan pengambilan keputusan yang tepat.

Rumus ini digunakan untuk mengukur penyebaran data, membandingkan kelompok data yang berbeda, dan mengidentifikasi pola dan tren dalam data.

Pengertian Ragam Data Kelompok

Ragam data kelompok mengacu pada kumpulan data yang terdiri dari beberapa pengamatan terkait yang mewakili satu kesatuan atau entitas tertentu. Setiap pengamatan dalam kelompok tersebut merupakan variabel yang memberikan informasi tentang aspek atau karakteristik tertentu dari entitas tersebut.

Karakteristik Ragam Data Kelompok

• Memiliki Struktur Hirarkis: Data dikelompokkan menjadi beberapa tingkatan, di mana setiap tingkat mewakili aspek yang lebih spesifik dari entitas.
• Ketergantungan Antar Variabel: Variabel dalam satu kelompok saling bergantung dan memberikan informasi bersama tentang entitas yang diwakili.
• Memiliki Hubungan yang Jelas: Hubungan antara pengamatan dalam kelompok jelas dan terdefinisi, sehingga memudahkan analisis dan interpretasi data.

Jenis-Jenis Ragam Data Kelompok

Ragam data kelompok merupakan kumpulan data yang dikelompokkan berdasarkan karakteristik tertentu. Terdapat dua jenis utama ragam data kelompok, yaitu:

Ragam Data Nominal

Ragam data nominal mengelompokkan data ke dalam kategori yang berbeda, tanpa adanya urutan atau hubungan hierarki. Setiap kategori mewakili nilai yang berbeda, dan data tidak dapat dioperasikan secara matematis.

• Contoh: Jenis kelamin (laki-laki, perempuan)
• Contoh: Warna (merah, biru, hijau)

Ragam Data Ordinal

Ragam data ordinal mengelompokkan data ke dalam kategori yang berbeda, dengan urutan atau hubungan hierarki yang jelas. Namun, perbedaan antara kategori tidak dapat diukur secara pasti.

• Contoh: Tingkat pendidikan (SD, SMP, SMA, Universitas)

li>Contoh: Tingkat kepuasan (sangat tidak puas, tidak puas, puas, sangat puas)

Rumus Ragam Data Kelompok

Ragam data kelompok adalah ukuran seberapa menyebar data dalam suatu kelompok. Rumusnya berbeda-beda tergantung pada jenis data yang digunakan.

Untuk data numerik, rumus ragam data kelompok adalah:

$$s^2 = \frac\sum_i=1^n(x_i

\barx)^2n-1$$

di mana:

• $s^2$ adalah ragam data kelompok
• $x_i$ adalah nilai data ke-$i$
• $\barx$ adalah mean data
• $n$ adalah jumlah data

Untuk data kategorik, rumus ragam data kelompok adalah:

$$s^2 = \sum_i=1^k p_i (1

p_i)$$

di mana:

• $s^2$ adalah ragam data kelompok
• $p_i$ adalah proporsi data yang termasuk dalam kategori ke-$i$
• $k$ adalah jumlah kategori

Tabel berikut merangkum rumus ragam data kelompok untuk berbagai jenis data:

Jenis Data	Rumus Ragam Data Kelompok
Numerik	$$s^2 = \frac\sum_i=1^n(x_i \barx)^2n-1$$
Kategorik	$$s^2 = \sum_i=1^k p_i (1 p_i)$$

Contoh Penerapan Rumus Ragam Data Kelompok

Rumus ragam data kelompok digunakan untuk menghitung variabilitas data dalam kelompok yang berbeda. Berikut langkah-langkah penerapan rumus ini:

1. Hitung rata-rata (mean) dari setiap kelompok.
2. Hitung selisih kuadrat dari setiap data dalam kelompok terhadap rata-rata kelompoknya.
3. Jumlahkan selisih kuadrat dari semua kelompok.
4. Bagi jumlah selisih kuadrat dengan jumlah derajat kebebasan, yaitu (n
   

   k), di mana n adalah jumlah total data dan k adalah jumlah kelompok.

Berikut contoh soal penerapan rumus ragam data kelompok:

Terdapat tiga kelompok data dengan jumlah anggota masing-masing 10, 12, dan 15. Rata-rata data untuk setiap kelompok adalah 10, 12, dan 14. Hitunglah ragam data kelompok.

1. Selisih kuadrat kelompok 1: (10
   • 10)^2 + (11
   • 10)^2 + … + (15
   • 10)^2 = 100
2. Selisih kuadrat kelompok 2: (12
   • 12)^2 + (13
   • 12)^2 + … + (17
   • 12)^2 = 120
3. Selisih kuadrat kelompok 3: (14
   • 14)^2 + (15
   • 14)^2 + … + (19
   • 14)^2 = 150

Jumlah selisih kuadrat: 100 + 120 + 150 = 370

Derajat kebebasan: (10 + 12 + 15 – 3) = 37

Ragam data kelompok: 370 / 37 = 10

“Ragam data kelompok mengukur variabilitas data dalam setiap kelompok, dan dapat digunakan untuk membandingkan variabilitas antara kelompok.”

Manfaat Penggunaan Rumus Ragam Data Kelompok

Rumus ragam data kelompok memainkan peran penting dalam analisis data, memberikan wawasan berharga tentang variabilitas data dalam suatu kelompok.

Rumus ini memungkinkan peneliti dan analis untuk mengukur penyebaran data, mengidentifikasi pola, dan membuat kesimpulan yang lebih tepat.

Manfaat Utama

• Mengukur Variabilitas Data: Rumus ragam data kelompok memberikan ukuran kuantitatif tentang seberapa tersebar data dalam suatu kelompok.
• Membandingkan Kelompok Data: Rumus ini memungkinkan perbandingan variabilitas antara dua atau lebih kelompok data, membantu mengidentifikasi perbedaan atau kesamaan yang signifikan.
• Menentukan Signifikansi Statistik: Ragam data kelompok dapat digunakan untuk menentukan apakah perbedaan antara kelompok data signifikan secara statistik, memberikan dasar yang kuat untuk menarik kesimpulan.
• Membuat Prediksi: Memahami variabilitas data memungkinkan peneliti membuat prediksi yang lebih akurat tentang kemungkinan hasil atau tren di masa depan.
• Mengoptimalkan Proses: Dengan mengukur variabilitas, organisasi dapat mengidentifikasi area yang memerlukan perbaikan dan mengoptimalkan proses mereka.

Ilustrasi Praktis

Sebagai ilustrasi, pertimbangkan sebuah perusahaan yang ingin menganalisis data penjualan dari dua cabang yang berbeda. Menggunakan rumus ragam data kelompok, perusahaan dapat menentukan seberapa besar perbedaan variabilitas penjualan antara kedua cabang.

Jika satu cabang menunjukkan variabilitas penjualan yang lebih tinggi, hal ini dapat menunjukkan adanya faktor yang mempengaruhi penjualan, seperti strategi pemasaran yang kurang efektif atau pelatihan staf yang tidak memadai. Perusahaan kemudian dapat menyelidiki lebih lanjut dan menerapkan langkah-langkah untuk mengatasi masalah tersebut.

Kesimpulan Akhir

Secara keseluruhan, rumus ragam data kelompok merupakan alat yang berharga untuk menganalisis data dan memahami penyebarannya. Dengan menerapkan rumus ini dengan benar, peneliti dan analis dapat memperoleh wawasan yang berharga dan membuat kesimpulan yang lebih tepat.

Pertanyaan Umum (FAQ)

Apa saja jenis-jenis ragam data kelompok?

Ada dua jenis utama ragam data kelompok: ragam populasi dan ragam sampel.

Bagaimana cara menggunakan rumus ragam data kelompok?

Untuk menggunakan rumus ragam data kelompok, Anda perlu mengetahui nilai rata-rata dan data individu dalam kumpulan data.

Apa saja manfaat penggunaan rumus ragam data kelompok?

Manfaat penggunaan rumus ragam data kelompok antara lain: mengidentifikasi pola dan tren, membandingkan kelompok data, dan membuat inferensi statistik.