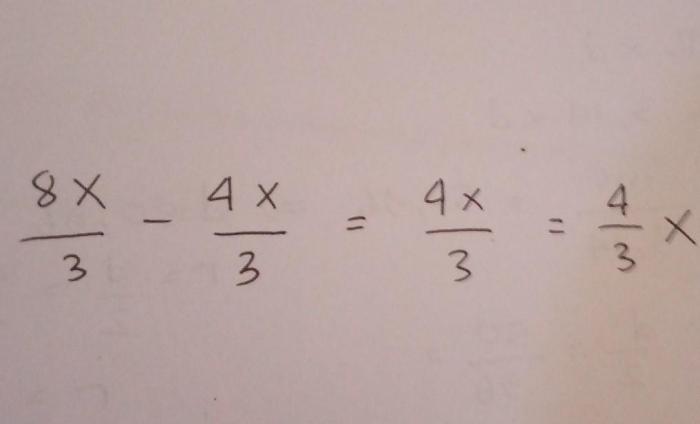Sederhanakan bentuk bentuk aljabar berikut – Sederhanakan bentuk aljabar berikut adalah proses penting dalam matematika yang melibatkan penyederhanaan ekspresi aljabar kompleks menjadi bentuk yang lebih sederhana dan mudah dipahami. Proses ini banyak digunakan dalam berbagai bidang, mulai dari matematika dasar hingga fisika dan teknik.

Dengan menyederhanakan bentuk aljabar, kita dapat mengidentifikasi pola, menyelesaikan persamaan, dan memahami hubungan antara variabel dan konstanta dengan lebih mudah.

Definisi Sederhanakan Bentuk Aljabar

Sederhanakan bentuk aljabar berarti memanipulasi ekspresi aljabar untuk mendapatkan bentuk yang lebih sederhana dan mudah dipahami. Bentuk aljabar sederhana umumnya terdiri dari suku-suku yang tidak dapat disederhanakan lebih lanjut.

Contoh bentuk aljabar sederhana adalah 2x + 3, sedangkan contoh bentuk aljabar kompleks adalah (x + 2)(x – 3).

Operasi Sederhanakan Bentuk Aljabar

Operasi umum yang digunakan untuk menyederhanakan bentuk aljabar meliputi:

• Menggabungkan suku-suku sejenis
• Menggunakan distributif
• Memfaktorkan
• Menggunakan identitas aljabar

Manfaat Menyederhanakan Bentuk Aljabar

Menyederhanakan bentuk aljabar memiliki beberapa manfaat, antara lain:

• Membuat ekspresi lebih mudah dipahami dan diinterpretasikan
• Memfasilitasi operasi aljabar lebih lanjut, seperti menyelesaikan persamaan atau pertidaksamaan
• Memungkinkan pengenalan pola dan hubungan dalam ekspresi aljabar

Contoh Penyederhanaan Bentuk Aljabar

Sebagai contoh, mari kita sederhanakan bentuk aljabar 2x + 3x – 5:

• Gabungkan suku-suku sejenis: 2x + 3x = 5x
• Bentuk sederhana: 5x – 5

Teknik Penyederhanaan

Penyederhanaan bentuk aljabar adalah proses memodifikasi ekspresi aljabar menjadi bentuk yang lebih sederhana tanpa mengubah nilainya. Teknik dasar penyederhanaan meliputi:

Menggabungkan Suku Sejenis, Sederhanakan bentuk bentuk aljabar berikut

Menggabungkan suku sejenis melibatkan penambahan atau pengurangan koefisien dari suku-suku yang memiliki variabel yang sama dan pangkat yang sama. Misalnya, 2x + 5x dapat disederhanakan menjadi 7x.

Memfaktorkan Ekspresi

Memfaktorkan ekspresi melibatkan mengekspresikan ekspresi sebagai hasil kali dari faktor-faktornya. Misalnya, x^2 – 9 dapat difaktorkan menjadi (x + 3)(x – 3).

Dalam proses penyederhanaan bentuk aljabar, pemahaman tentang konsep dasar sangat penting. Sebagai contoh, untuk menentukan panjang AG dari sebuah bangunan, kita perlu terlebih dahulu menyederhanakan bentuk aljabar yang mewakili panjang tersebut ( tentukan panjang ag dari bangunan berikut ). Dengan menyederhanakan bentuk aljabar tersebut, kita dapat memperoleh persamaan yang lebih sederhana dan mudah untuk dipecahkan, sehingga memungkinkan kita untuk menentukan nilai AG dengan lebih mudah.

Menggunakan Sifat-sifat Eksponen

Sifat-sifat eksponen dapat digunakan untuk menyederhanakan ekspresi yang berisi pangkat. Sifat-sifat ini meliputi:

• a^m – a^n = a^(m + n)
• (a^m)^n = a^(m – n)
• a^0 = 1

Langkah-langkah Penyederhanaan Bentuk Aljabar: Sederhanakan Bentuk Bentuk Aljabar Berikut

Penyederhanaan bentuk aljabar adalah proses mengubah ekspresi aljabar menjadi bentuk yang lebih sederhana tanpa mengubah nilainya. Langkah-langkah sistematis untuk menyederhanakan bentuk aljabar meliputi:

Pengelompokan Suku Sejenis

Kelompokkan suku-suku yang memiliki variabel dan eksponen yang sama. Gabungkan koefisiennya untuk mendapatkan suku yang lebih sederhana.

Pengurangan Suku Sejenis

Jika terdapat suku-suku sejenis dengan tanda yang berbeda, kurangkan koefisiennya dan pertahankan variabel dan eksponennya.

Penggunaan Distributif

Kalikan setiap suku dalam kurung dengan faktor di luar kurung dan jumlahkan hasilnya untuk menyederhanakan ekspresi.

Proses penyederhanaan bentuk aljabar bertujuan untuk menyajikan ekspresi aljabar dalam bentuk yang lebih sederhana. Sementara itu, dalam konteks produksi, terdapat beberapa tahap yang terlibat. Tahap-tahap ini mencakup perencanaan, pengadaan, pembuatan, dan distribusi. Dengan demikian, tahap yang tidak termasuk dalam tahap produksi adalah tahap yang berada di luar cakupan proses produksi itu sendiri, seperti tahap penelitian dan pengembangan atau pemasaran.

Pemfaktoran

Faktorkan ekspresi aljabar menjadi faktor-faktor yang lebih kecil. Ini dapat menyederhanakan ekspresi dan memudahkan operasi lebih lanjut.

Pembagian Polinomial

Untuk ekspresi dalam bentuk pecahan polinomial, bagi polinomial pembilang dengan polinomial penyebut menggunakan pembagian panjang atau metode sintetis.

Contoh Penyederhanaan Bentuk Aljabar

Penyederhanaan bentuk aljabar adalah proses mengganti ekspresi yang kompleks dengan ekspresi yang lebih sederhana dan setara.

Dalam menyederhanakan bentuk aljabar, kita dapat menggunakan prinsip-prinsip dasar aljabar untuk menggabungkan suku-suku yang serupa. Struktur lembaga negara setelah amandemen juga mengalami penyederhanaan dan penggabungan, sebagaimana dijelaskan dalam struktur lembaga negara setelah amandemen . Proses penyederhanaan ini bertujuan untuk menciptakan sistem pemerintahan yang lebih efisien dan efektif.

Dengan demikian, baik dalam aljabar maupun dalam struktur lembaga negara, penyederhanaan bertujuan untuk mengoptimalkan fungsi dan meningkatkan efisiensi.

Untuk menyederhanakan bentuk aljabar, kita dapat menggunakan berbagai sifat operasi aljabar, seperti:

• Distributif
• Asosiatif
• Komutatif
• Identitas
• Invers

Dengan menerapkan sifat-sifat ini, kita dapat menyederhanakan ekspresi aljabar dengan:

• Menggabungkan suku-suku sejenis
• Memfaktorkan ekspresi
• Menggunakan rumus identitas
• Membagi dengan suku-suku yang sama

Proses penyederhanaan ini sangat penting dalam aljabar karena memungkinkan kita untuk menyelesaikan persamaan, memanipulasi ekspresi, dan memperoleh pemahaman yang lebih baik tentang sifat-sifat bilangan dan operasi aljabar.

Aplikasi Penyederhanaan

Penyederhanaan bentuk aljabar memiliki banyak aplikasi praktis di berbagai bidang:

Matematika

Dalam matematika, penyederhanaan bentuk aljabar sangat penting untuk:

• Memecahkan persamaan dan pertidaksamaan
• Memfaktorkan polinomial
• Menyederhanakan ekspresi aljabar yang kompleks

Ilmu Pengetahuan

Dalam ilmu pengetahuan, penyederhanaan bentuk aljabar digunakan untuk:

• Membuat model matematis dari fenomena dunia nyata
• Menyelesaikan masalah dalam fisika, kimia, dan biologi
• Menganalisis data dan membuat prediksi

Kehidupan Sehari-hari

Dalam kehidupan sehari-hari, penyederhanaan bentuk aljabar dapat digunakan untuk:

• Memecahkan masalah keuangan, seperti menghitung bunga dan pembayaran cicilan
• Menyederhanakan resep dan instruksi
• Memahami konsep matematika dasar

Penutupan

Kemampuan menyederhanakan bentuk aljabar sangat penting untuk kesuksesan dalam matematika dan bidang terkait. Dengan memahami teknik dan langkah-langkah yang diuraikan dalam artikel ini, pembaca akan dilengkapi dengan alat yang berharga untuk menguasai ekspresi aljabar dan memecahkan masalah matematika yang kompleks.

Pertanyaan dan Jawaban

Apa itu penyederhanaan bentuk aljabar?

Penyederhanaan bentuk aljabar adalah proses mengubah ekspresi aljabar kompleks menjadi bentuk yang lebih sederhana dan mudah dipahami.

Mengapa penyederhanaan bentuk aljabar penting?

Penyederhanaan bentuk aljabar penting untuk mengidentifikasi pola, menyelesaikan persamaan, dan memahami hubungan antara variabel dan konstanta.

Apa saja teknik yang digunakan untuk menyederhanakan bentuk aljabar?

Teknik yang umum digunakan untuk menyederhanakan bentuk aljabar meliputi menggabungkan suku sejenis, memfaktorkan ekspresi, dan menggunakan sifat-sifat eksponen.