Persamaan eksponen memainkan peran penting dalam berbagai bidang, mulai dari matematika hingga fisika. Persamaan ini melibatkan variabel yang dipangkatkan, dan menyelesaikannya membutuhkan pemahaman mendalam tentang konsep eksponen.
Dalam panduan ini, kita akan menguraikan cara menyelesaikan persamaan eksponen secara efektif, membahas metode umum seperti logaritma dan eksponen yang sama. Selain itu, kita akan memberikan contoh langkah demi langkah, tips untuk menyederhanakan proses, dan mengeksplorasi aplikasi praktis persamaan eksponen.
Pengertian Persamaan Eksponen
Persamaan eksponen adalah persamaan yang melibatkan variabel yang dipangkatkan dengan angka lain, yang dikenal sebagai basis. Umumnya, persamaan eksponen ditulis dalam bentuk a^x = b, di mana a adalah basis, x adalah eksponen, dan b adalah nilai konstanta.
Perbedaan utama antara basis dan eksponen adalah basis mewakili angka yang dipangkatkan, sedangkan eksponen menunjukkan berapa kali basis dikalikan dengan dirinya sendiri. Misalnya, dalam persamaan 2^3 = 8, basisnya adalah 2 dan eksponennya adalah 3, yang menunjukkan bahwa 2 dikalikan dengan dirinya sendiri sebanyak 3 kali, menghasilkan nilai 8.
Cara Menyelesaikan Persamaan Eksponen

Persamaan eksponen adalah persamaan yang pangkatnya merupakan variabel yang tidak diketahui. Untuk menyelesaikan persamaan eksponen, kita dapat menggunakan dua metode utama: metode logaritma dan metode eksponen yang sama.
Metode Logaritma
Metode logaritma melibatkan pengambilan logaritma kedua sisi persamaan. Ini mengubah persamaan eksponen menjadi persamaan linier yang dapat diselesaikan untuk variabel yang tidak diketahui.Langkah-langkah menyelesaikan persamaan eksponen menggunakan logaritma:
- Ambil logaritma kedua sisi persamaan dengan basis yang sama.
- Sederhanakan menggunakan sifat logaritma.
- Pecahkan persamaan linier yang dihasilkan untuk variabel yang tidak diketahui.
Contoh:Selesaikan persamaan eksponen: 2 x = 8Mengambil logaritma kedua sisi dengan basis 2:log 2 (2 x ) = log 2 (8)Menyederhanakan:x = log 2 (8)Mengevaluasi:x = 3
Metode Eksponen yang Sama
Metode eksponen yang sama melibatkan mengekspresikan kedua sisi persamaan dalam eksponen yang sama. Ini memungkinkan kita untuk membandingkan basis dan eksponen untuk menemukan nilai variabel yang tidak diketahui.Langkah-langkah menyelesaikan persamaan eksponen dengan eksponen yang sama:
- Ekspresikan kedua sisi persamaan dalam eksponen yang sama.
- Bandingkan basis dan eksponen untuk menemukan nilai variabel yang tidak diketahui.
Contoh:Selesaikan persamaan eksponen: 3 x-1 = 27Mengekspresikan kedua sisi dalam eksponen 3:
x-1 = 3 3
Membandingkan eksponen:x-1 = 3Memecahkan untuk x:x = 4
Contoh Penyelesaian
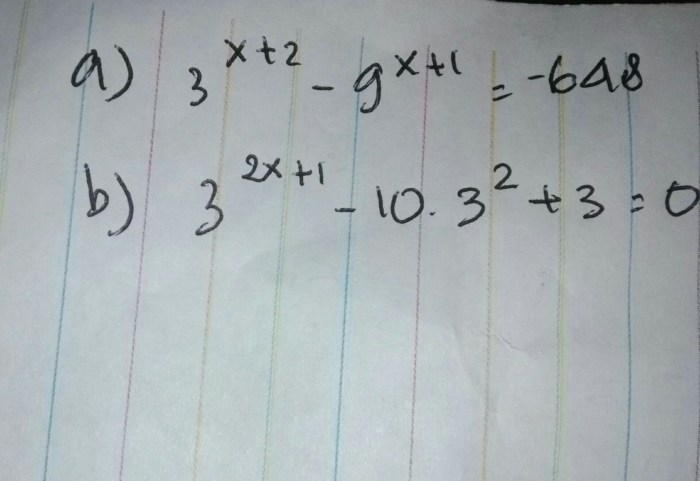
Berikut adalah contoh penyelesaian persamaan eksponen dengan langkah demi langkah:
Metode Logaritma
- Contoh 1: Selesaikan 2^x = 8
- Langkah 1: Ambil logaritma kedua sisi persamaan dengan basis 2.
- Langkah 2: Gunakan sifat logaritma: loga(ab) = b.
- Langkah 3: Selesaikan untuk x.
- Hasil: x = 3
Metode Eksponen yang Sama
- Contoh 2: Selesaikan 3x-1 = 9
- Langkah 1: Tulis ulang 9 sebagai pangkat 3.
- Langkah 2: Persamaan kedua sisi dengan basis yang sama, yaitu 3.
- Langkah 3: Selesaikan untuk x.
- Hasil: x = 2
Tabel Ringkasan
| Persamaan | Metode | Solusi |
|---|---|---|
| 2^x = 8 | Logaritma | x = 3 |
| 3x-1 = 9 | Eksponen yang Sama | x = 2 |
Tips dan Trik

Menyelesaikan persamaan eksponen dapat menjadi tugas yang menantang. Namun, ada beberapa tips dan trik yang dapat mempermudah proses ini:
Konversikan ke Bentuk Eksponensial: Ubah persamaan ke bentuk eksponensial dengan basis yang sama untuk mempermudah penyelesaian. Misalnya, persamaan 2x = 16 dapat dikonversi menjadi 2x = 2^4.
Mengatasi Persamaan Eksponen Kompleks
- Identifikasi Basis yang Sama: Untuk menyelesaikan persamaan dengan basis berbeda, cari cara untuk mengonversinya ke basis yang sama. Misalnya, persamaan 3x = 2^x dapat dikonversi menjadi 3x = (2^1)^x.
- Gunakan Sifat Logaritma: Logaritma dapat digunakan untuk menyelesaikan persamaan eksponen. Misalnya, persamaan 5x = 125 dapat diselesaikan dengan mengambil logaritma kedua sisi.
- Gunakan Sifat Eksponen: Sifat eksponen, seperti a^b
– a^c = a^(b+c), dapat digunakan untuk menyederhanakan persamaan dan menemukan solusi.
Aplikasi Persamaan Eksponen
Persamaan eksponen memiliki aplikasi luas dalam berbagai bidang, termasuk matematika, fisika, dan keuangan. Persamaan ini digunakan untuk memodelkan berbagai fenomena, seperti pertumbuhan populasi, peluruhan radioaktif, dan pertumbuhan investasi.
Dalam Matematika
Dalam matematika, persamaan eksponen digunakan untuk menyelesaikan masalah yang melibatkan pertumbuhan atau peluruhan eksponensial. Misalnya, persamaan $$y = a \cdot b^x$$ dapat digunakan untuk memodelkan pertumbuhan bakteri, di mana $$y$$ adalah jumlah bakteri pada waktu $$x$$, $$a$$ adalah jumlah awal bakteri, dan $$b$$ adalah tingkat pertumbuhan.
Dalam Fisika
Dalam fisika, persamaan eksponen digunakan untuk memodelkan fenomena seperti peluruhan radioaktif dan gelombang elektromagnetik. Misalnya, persamaan $$y = a \cdot e^-kx$$ dapat digunakan untuk memodelkan peluruhan radioaktif, di mana $$y$$ adalah jumlah zat radioaktif yang tersisa pada waktu $$x$$, $$a$$ adalah jumlah awal zat radioaktif, dan $$k$$ adalah konstanta peluruhan.
Dalam Keuangan
Dalam keuangan, persamaan eksponen digunakan untuk memodelkan pertumbuhan investasi dan suku bunga. Misalnya, persamaan $$y = P \cdot (1 + r)^x$$ dapat digunakan untuk memodelkan pertumbuhan investasi, di mana $$y$$ adalah nilai investasi pada waktu $$x$$, $$P$$ adalah nilai awal investasi, dan $$r$$ adalah tingkat bunga.
Contoh Nyata
Dalam kehidupan sehari-hari, persamaan eksponen dapat digunakan untuk:
- Memprediksi pertumbuhan populasi
- Menghitung peluruhan obat dalam tubuh
- Memprediksi pertumbuhan investasi
- Menganalisis data tren
- Memecahkan masalah teknik dan sains
Akhir Kata

Dengan memahami teknik yang disajikan dalam panduan ini, Anda akan dilengkapi dengan alat yang ampuh untuk memecahkan persamaan eksponen dengan percaya diri. Pengetahuan ini tidak hanya memperluas pemahaman matematika Anda tetapi juga membuka pintu ke aplikasi yang lebih luas dalam bidang lain.
Pertanyaan Umum (FAQ)
Apa perbedaan antara basis dan eksponen dalam persamaan eksponen?
Basis adalah angka yang dipangkatkan, sedangkan eksponen adalah angka kecil yang menunjukkan berapa kali basis dikalikan dengan dirinya sendiri.
Apa metode yang paling umum digunakan untuk menyelesaikan persamaan eksponen?
Dua metode umum adalah logaritma dan eksponen yang sama.
Apakah ada strategi khusus untuk menyelesaikan persamaan eksponen yang kompleks?
Ya, strategi seperti mengubah persamaan menjadi bentuk standar atau memecahnya menjadi persamaan yang lebih sederhana dapat membantu.
