Simpangan baku dari data 3 6 4 7 5 adalah – Dalam statistik, simpangan baku dari data 3, 6, 4, 7, 5 adalah ukuran penting yang menggambarkan variabilitas data. Ini memberikan wawasan tentang seberapa tersebar data di sekitar nilai rata-ratanya.

Konsep simpangan baku sangat penting dalam berbagai bidang, termasuk keuangan, sains, dan manufaktur. Ini membantu peneliti dan praktisi dalam memahami penyebaran data, mengidentifikasi tren, dan membuat prediksi yang lebih baik.

Pengertian Simpangan Baku

Simpangan baku adalah ukuran seberapa tersebar data dari rata-rata atau mean. Ini mengukur variabilitas dalam suatu kumpulan data dan merupakan metrik penting dalam statistik.

Simpangan baku dihitung sebagai akar kuadrat dari varians, yang merupakan rata-rata kuadrat dari selisih antara setiap titik data dan mean.

Formula Simpangan Baku

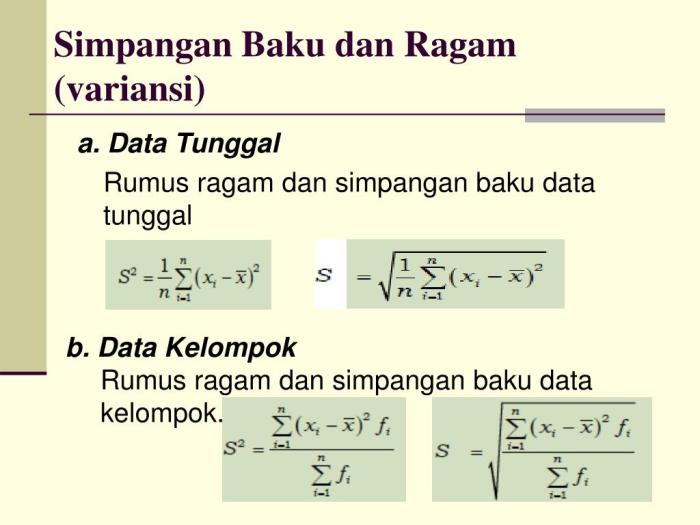
Simpangan baku (σ) dihitung menggunakan rumus berikut:

σ = √(Σ(x

Simpangan baku dari data 3, 6, 4, 7, dan 5 adalah 1,58. Dalam konteks agama, terdapat sebuah ungkapan bahwa “sesungguhnya aku sesuai prasangka hambaku” ( sesungguhnya aku sesuai prasangka hambaku ). Artinya, Tuhan akan memperlakukan hamba-Nya sesuai dengan keyakinan dan prasangka mereka terhadap-Nya.

Jika hamba yakin bahwa Tuhan Maha Baik, maka Tuhan akan memperlakukannya dengan baik. Demikian pula, jika hamba yakin bahwa Tuhan Maha Kuasa, maka Tuhan akan menunjukkan kuasa-Nya dalam kehidupan hamba tersebut. Hal ini sejalan dengan konsep simpangan baku, yang menunjukkan seberapa besar data menyebar dari nilai rata-ratanya.

Sama seperti keyakinan dan prasangka hamba yang memengaruhi perlakuan Tuhan, simpangan baku menggambarkan variasi data yang memengaruhi nilai rata-ratanya.

μ)² / N)

Simpangan baku dari data 3 6 4 7 5 adalah 1,58. Sebagaimana yang dibahas dalam resensi buku Habis Gelap Terbitlah Terang , data statistik dapat digunakan untuk menganalisis fenomena sosial. Dalam konteks ini, simpangan baku menunjukkan penyebaran data di sekitar nilai rata-ratanya, sehingga memberikan wawasan tentang variabilitas data.

• σ adalah simpangan baku
• x adalah titik data
• μ adalah mean
• N adalah jumlah titik data

Contoh Perhitungan Simpangan Baku

Untuk menghitung simpangan baku dari kumpulan data 3, 6, 4, 7, dan 5, kita dapat menggunakan rumus berikut:

1. Hitung mean: (3 + 6 + 4 + 7 + 5) / 5 = 5
2. Hitung selisih antara setiap titik data dan mean: (3
   • 5)², (6
   • 5)², (4
   • 5)², (7
   • 5)², (5
   • 5)²
3. Hitung kuadrat dari selisih: 4, 1, 1, 4, 0
4. Jumlahkan kuadrat dari selisih: 10
5. Hitung varians: 10 / 5 = 2
6. Hitung simpangan baku: √2 = 1,41

Jadi, simpangan baku dari kumpulan data yang diberikan adalah 1,41.

Rumus Simpangan Baku

Simpangan baku adalah ukuran penyebaran data. Rumus simpangan baku untuk data yang tidak dikelompokkan adalah:

σ = √[Σ(x

μ)² / N]

Dimana:

• σ adalah simpangan baku
• x adalah nilai data
• μ adalah nilai rata-rata
• N adalah jumlah data

Untuk menghitung simpangan baku, pertama-tama hitung nilai rata-rata data. Kemudian, hitung selisih antara setiap nilai data dan nilai rata-rata. Kuadratkan setiap selisih ini. Terakhir, jumlahkan semua kuadrat selisih dan bagi dengan jumlah data. Akar kuadrat dari hasil ini adalah simpangan baku.

Simpangan baku dari data 3, 6, 4, 7, dan 5 adalah 1,58. Dalam fisika, simpangan baku merupakan ukuran penyebaran data dari nilai rata-ratanya. Konsep ini juga diterapkan pada berbagai bidang, termasuk kelistrikan. Misalnya, sebuah kumparan yang terdiri dari 1000 lilitan dapat menghasilkan simpangan baku tegangan atau arus yang berbeda tergantung pada faktor-faktor seperti frekuensi dan beban.

Pemahaman tentang simpangan baku sangat penting dalam analisis data dan desain sistem untuk memastikan kinerja yang optimal.

Perhitungan Simpangan Baku

Simpangan baku adalah ukuran seberapa jauh data menyebar dari nilai rata-rata. Simpangan baku yang lebih tinggi menunjukkan bahwa data lebih menyebar, sedangkan simpangan baku yang lebih rendah menunjukkan bahwa data lebih terpusat di sekitar rata-rata.

Langkah-langkah Menghitung Simpangan Baku

• Hitung mean (rata-rata) dari data.
• Hitung kuadrat dari selisih setiap data dengan mean.
• Jumlahkan kuadrat selisih tersebut.
• Bagi jumlah tersebut dengan jumlah data.
• Hitung akar kuadrat dari hasil pembagian tersebut.

Contoh Perhitungan

Untuk data 3, 6, 4, 7, 5, meannya adalah 5.

Kuadrat selisih setiap data dengan mean:

• (3 – 5)^2 = 4
• (6 – 5)^2 = 1
• (4 – 5)^2 = 1
• (7 – 5)^2 = 4
• (5 – 5)^2 = 0

Jumlah kuadrat selisih: 10

Rata-rata kuadrat selisih: 10 / 5 = 2

Simpangan baku: √2 = 1,41

Interpretasi Simpangan Baku

Simpangan baku 1,41 menunjukkan bahwa data cukup menyebar dari rata-rata 5. Ini berarti bahwa sebagian besar data berada dalam kisaran 5 ± 1,41, yaitu antara 3,59 dan 6,41.

Interpretasi Simpangan Baku

Simpangan baku adalah ukuran penyebaran data yang menunjukkan seberapa jauh nilai data tersebar dari nilai rata-rata. Nilai simpangan baku yang rendah menunjukkan bahwa data berkerumun di sekitar nilai rata-rata, sementara nilai simpangan baku yang tinggi menunjukkan bahwa data tersebar lebih luas.

Interpretasi Nilai Simpangan Baku Rendah

• Nilai simpangan baku yang rendah menunjukkan bahwa data berkerumun dekat dengan nilai rata-rata.
• Hal ini menunjukkan bahwa sebagian besar data memiliki nilai yang serupa dengan nilai rata-rata.

Interpretasi Nilai Simpangan Baku Tinggi

• Nilai simpangan baku yang tinggi menunjukkan bahwa data tersebar lebih luas dari nilai rata-rata.
• Hal ini menunjukkan bahwa terdapat perbedaan yang lebih besar antara nilai data.

Contoh Aplikasi Simpangan Baku

Simpangan baku adalah ukuran variabilitas yang banyak digunakan dalam berbagai bidang, mulai dari keuangan hingga sains.

Bidang Keuangan

Dalam keuangan, simpangan baku digunakan untuk mengukur risiko investasi. Misalnya, saham dengan simpangan baku yang tinggi menunjukkan bahwa harga sahamnya cenderung berfluktuasi secara signifikan, sehingga berisiko lebih tinggi dibandingkan saham dengan simpangan baku yang rendah.

Bidang Sains

Dalam sains, simpangan baku digunakan untuk menganalisis data eksperimen. Misalnya, dalam percobaan yang mengukur waktu yang dibutuhkan tikus untuk menyelesaikan labirin, simpangan baku menunjukkan seberapa bervariasi waktu penyelesaiannya. Simpangan baku yang tinggi menunjukkan bahwa ada variasi yang besar dalam waktu penyelesaian, sementara simpangan baku yang rendah menunjukkan bahwa tikus menyelesaikan labirin dalam waktu yang relatif sama.

Pengambilan Keputusan

Simpangan baku juga membantu dalam pengambilan keputusan. Misalnya, seorang manajer perekrutan mungkin menggunakan simpangan baku untuk membandingkan hasil tes keterampilan pelamar. Pelamar dengan skor tes yang tinggi dan simpangan baku yang rendah menunjukkan konsistensi dan kemampuan yang kuat, sementara pelamar dengan skor tes yang tinggi dan simpangan baku yang tinggi menunjukkan variasi yang lebih besar dalam kinerja mereka.

Simpangan Baku

Simpangan baku adalah ukuran seberapa banyak data menyebar di sekitar nilai rata-rata. Semakin besar simpangan baku, semakin tersebar data.

Rumus Simpangan Baku, Simpangan baku dari data 3 6 4 7 5 adalah

Rumus simpangan baku untuk kumpulan data yang tidak dikelompokkan adalah:

σ = √(Σ(x

μ)² / N)

di mana:

• σ adalah simpangan baku
• x adalah setiap nilai data
• μ adalah rata-rata data
• N adalah jumlah data

Contoh

Untuk data 3, 6, 4, 7, 5, rata-rata (μ) adalah 5.

Simpangan baku (σ) dapat dihitung sebagai:

σ = √((3

• 5)² + (6
• 5)² + (4
• 5)² + (7
• 5)² + (5
• 5)² / 5)

σ = √(4 + 1 + 1 + 4 + 0 / 5) = 2

Jadi, simpangan baku dari data yang diberikan adalah 2.

Penutup: Simpangan Baku Dari Data 3 6 4 7 5 Adalah

Dengan memahami simpangan baku, kita dapat memperoleh pemahaman yang lebih baik tentang karakteristik data dan membuat keputusan yang lebih tepat berdasarkan data tersebut. Ini adalah alat statistik yang ampuh yang dapat memberikan wawasan berharga tentang variabilitas dan distribusi data.

Pertanyaan yang Sering Muncul

Apa yang dimaksud dengan simpangan baku?

Simpangan baku adalah ukuran statistik yang menunjukkan seberapa jauh data tersebar dari nilai rata-ratanya.

Bagaimana cara menghitung simpangan baku?

Rumus simpangan baku untuk data yang tidak dikelompokkan adalah akar kuadrat dari varians, yang dihitung dengan menjumlahkan kuadrat selisih setiap titik data dari rata-rata dan membaginya dengan jumlah titik data dikurangi satu.

Apa arti nilai simpangan baku yang tinggi?

Nilai simpangan baku yang tinggi menunjukkan bahwa data sangat tersebar dari nilai rata-ratanya.