Simpangan baku dari data 4 5 6 7 8 adalah ukuran statistik penting yang menggambarkan seberapa banyak titik data tersebar dari rata-ratanya. Ini adalah alat yang ampuh untuk menganalisis dan menafsirkan data dalam berbagai bidang.

Konsep simpangan baku sangat penting dalam statistik dan digunakan secara luas dalam bidang-bidang seperti keuangan, sains, dan teknik.

Pengertian Simpangan Baku

Simpangan baku adalah ukuran statistik yang mengukur seberapa tersebar data dari nilai rata-ratanya. Ini memberikan informasi tentang variabilitas data dan dapat digunakan untuk membandingkan set data yang berbeda.

Rumus Simpangan Baku, Simpangan baku dari data 4 5 6 7 8 adalah

Rumus untuk menghitung simpangan baku adalah:

Simpangan Baku (s) = √[(Σ(x – μ)²)/(n – 1)]

di mana:* x adalah nilai data

Simpangan baku dari data 4, 5, 6, 7, dan 8 adalah ukuran sebaran data. Dalam bidang kimia, konsep serupa digunakan untuk menyeimbangkan persamaan reaksi redoks, di mana jumlah atom dan muatan pada kedua sisi persamaan harus sama. Misalnya, dalam setarakan persamaan reaksi redoks berikut , jumlah atom oksigen pada sisi kiri dan kanan harus sama.

Setelah reaksi seimbang, simpangan baku dari data awal dapat digunakan kembali untuk menilai akurasi dan ketepatan hasil.

• μ adalah nilai rata-rata
• n adalah jumlah data

Contoh Simpangan Baku

Sebagai contoh, mari kita hitung simpangan baku dari data berikut: 4, 5, 6, 7, 8.* Nilai rata-rata (μ) = (4 + 5 + 6 + 7 + 8) / 5 = 6

• Varians = [(4
• 6)² + (5
• 6)² + (6
• 6)² + (7
• 6)² + (8
• 6)²] / (5
• 1) = 2
• Simpangan Baku (s) = √2 = 1,414

Ini menunjukkan bahwa data tersebut tersebar sekitar 1,414 unit dari nilai rata-rata 6.

Pentingnya Simpangan Baku

Simpangan baku memiliki beberapa kegunaan penting:

• Mengukur variabilitas data
• Membandingkan set data yang berbeda
• Membuat prediksi dan estimasi
• Menilai reliabilitas dan validitas pengukuran

Cara Menghitung Simpangan Baku

Simpangan baku adalah ukuran sebaran data yang menunjukkan seberapa jauh data tersebut menyimpang dari nilai rata-rata.

Rumus Simpangan Baku, Simpangan baku dari data 4 5 6 7 8 adalah

Rumus simpangan baku adalah:

$$s = \sqrt\frac\sum(x_i

\barx)^2N-1$$

di mana:

• $s$ adalah simpangan baku
• $x_i$ adalah nilai data ke-$i$
• $\barx$ adalah nilai rata-rata
• $N$ adalah jumlah data

Contoh Perhitungan

Untuk data 4, 5, 6, 7, 8:

Nilai rata-rata ($\barx$) = (4 + 5 + 6 + 7 + 8) / 5 = 6

Simpangan baku ($s$) =

$x_i$	$x_i \barx$	$(x_i Simpangan baku dari data 4, 5, 6, 7, dan 8 adalah 1,58. Angka ini mewakili penyebaran data seputar nilai rata-rata. Dalam konteks pintu masuk atau gerbang ke suatu kawasan , simpangan baku menunjukkan variasi jarak antara pintu masuk dan lokasi yang ditentukan, seperti titik pertemuan atau pusat kawasan. Dengan demikian, simpangan baku memberikan wawasan tentang kedekatan atau keterpencilan pintu masuk dari area lain dalam kawasan. \barx)^2$
4	-2	4
5	-1	1
6	0	0
7	1	1
8	2	4
		Total = 10

$$s = \sqrt\frac105-1 = \sqrt2.5 = 1.58$$

Interpretasi Simpangan Baku

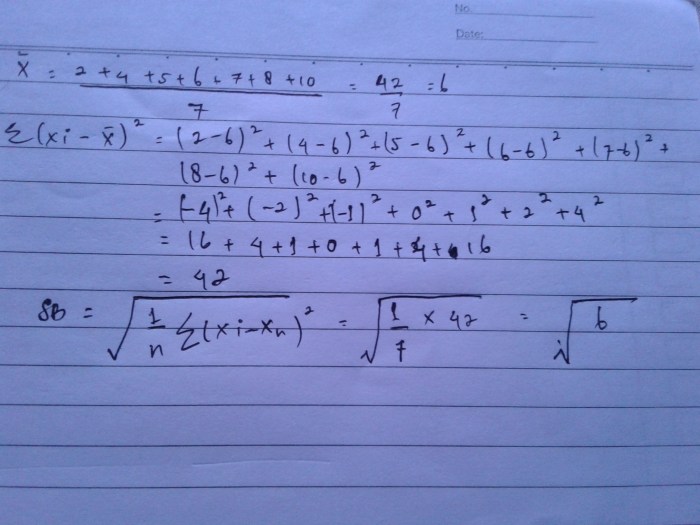
Simpangan baku adalah ukuran seberapa jauh data menyebar dari nilai rata-ratanya. Nilai simpangan baku yang lebih besar menunjukkan penyebaran data yang lebih luas, sementara nilai simpangan baku yang lebih kecil menunjukkan penyebaran data yang lebih sempit.

Hubungan antara Simpangan Baku dan Penyebaran Data

Penyebaran data dapat diklasifikasikan sebagai berikut:

• Penyebaran rendah:Nilai simpangan baku kurang dari 1.
• Penyebaran sedang:Nilai simpangan baku antara 1 dan 2.
• Penyebaran tinggi:Nilai simpangan baku lebih besar dari 2.

Penyebaran data yang rendah menunjukkan bahwa sebagian besar data berada dekat dengan nilai rata-rata, sementara penyebaran data yang tinggi menunjukkan bahwa data tersebar lebih luas dari nilai rata-rata.

Contoh Interpretasi Simpangan Baku

Dalam konteks data yang diberikan (4, 5, 6, 7, 8), nilai simpangan bakunya adalah 1,41. Hal ini menunjukkan bahwa data memiliki penyebaran sedang, karena nilai simpangan baku berada antara 1 dan 2.

Ini berarti bahwa sebagian besar data berada dalam kisaran 1,41 satuan standar deviasi dari nilai rata-rata (6). Dengan kata lain, sebagian besar data berada antara 4,59 dan 7,41.

Penerapan Simpangan Baku

Simpangan baku merupakan ukuran variabilitas dalam suatu kumpulan data. Penggunaannya sangat luas dalam berbagai bidang, termasuk statistik, manajemen risiko, dan pengendalian kualitas.

Analisis Statistik

Dalam analisis statistik, simpangan baku digunakan untuk mengukur penyebaran data di sekitar nilai rata-rata. Simpangan baku yang lebih kecil menunjukkan data yang lebih terkonsentrasi di sekitar rata-rata, sedangkan simpangan baku yang lebih besar menunjukkan data yang lebih tersebar.

Simpangan baku dari data 4, 5, 6, 7, dan 8 adalah ukuran sebaran data. Nilai rata-rata dari sekelompok bilangan, seperti yang disebutkan dalam rata rata sekelompok bilangan adalah 37 5 , dapat memberikan gambaran tentang pusat distribusi data. Simpangan baku melengkapi informasi ini dengan mengukur penyebaran data di sekitar rata-rata, memberikan pemahaman yang lebih komprehensif tentang distribusi data.

• Simpangan baku digunakan untuk menentukan interval kepercayaan, yang merupakan rentang nilai yang kemungkinan besar berisi nilai sebenarnya.
• Simpangan baku juga digunakan untuk melakukan uji hipotesis, yang merupakan metode statistik untuk menguji klaim tentang populasi.

Manajemen Risiko

Dalam manajemen risiko, simpangan baku digunakan untuk mengukur risiko yang terkait dengan suatu kejadian tertentu. Simpangan baku yang lebih tinggi menunjukkan risiko yang lebih besar.

• Simpangan baku digunakan untuk menghitung nilai-nilai-at-risk (VaR), yang merupakan jumlah kerugian maksimum yang dapat terjadi dengan tingkat probabilitas tertentu.
• Simpangan baku juga digunakan untuk mengembangkan model manajemen risiko yang dapat membantu organisasi mengidentifikasi dan mengelola risiko.

Pengendalian Kualitas

Dalam pengendalian kualitas, simpangan baku digunakan untuk mengukur variabilitas proses produksi. Simpangan baku yang lebih kecil menunjukkan proses yang lebih terkendali dan menghasilkan produk yang lebih konsisten.

• Simpangan baku digunakan untuk menetapkan batas kendali, yang merupakan rentang nilai yang dapat diterima untuk suatu proses.
• Simpangan baku juga digunakan untuk memantau proses produksi dan mengidentifikasi setiap penyimpangan dari norma.

Kesimpulan: Simpangan Baku Dari Data 4 5 6 7 8 Adalah

Secara keseluruhan, simpangan baku adalah alat penting untuk memahami dan menafsirkan data. Ini memberikan wawasan tentang variabilitas data dan membantu dalam membuat keputusan yang tepat berdasarkan analisis data.

Panduan FAQ

Apa itu simpangan baku?

Simpangan baku adalah ukuran statistik yang mengukur penyebaran data dari rata-ratanya.

Bagaimana cara menghitung simpangan baku?

Simpangan baku dihitung menggunakan rumus khusus yang melibatkan menghitung rata-rata data dan selisih kuadrat antara setiap titik data dan rata-rata.

Apa saja penerapan simpangan baku?

Simpangan baku digunakan dalam berbagai bidang, termasuk keuangan, sains, dan teknik, untuk menganalisis data dan membuat keputusan berdasarkan data.