Simpangan baku dari data 6 10 9 7 8 adalah ukuran statistik penting yang mengukur variabilitas data. Ini menunjukkan seberapa jauh titik data menyebar dari nilai rata-rata mereka, memberikan wawasan tentang distribusi data.
Konsep simpangan baku sangat penting dalam statistik, memungkinkan kita memahami karakteristik data dan membuat kesimpulan yang tepat.
Pengertian Simpangan Baku
Simpangan baku, juga dikenal sebagai deviasi standar, adalah ukuran sebaran data dalam statistik. Ini menunjukkan seberapa banyak nilai data berbeda dari rata-rata. Simpangan baku yang rendah menunjukkan bahwa data dikelompokkan dengan rapat di sekitar rata-rata, sedangkan simpangan baku yang tinggi menunjukkan bahwa data lebih tersebar.
Cara Menghitung Simpangan Baku
Rumus untuk menghitung simpangan baku adalah:
σ = √(Σ(x
μ)² / N)
Simpangan baku dari data 6, 10, 9, 7, dan 8 adalah 1,63. Beralih ke topik lain, jika kita memiliki bangun ruang dengan rumus volume tertentu, kita dapat menghitung volume tersebut menggunakan metode yang sesuai. Sebagai contoh, kita dapat hitunglah volume bangun ruang di bawah ini menggunakan integral atau rumus geometri.
Kembali ke simpangan baku, nilai 1,63 menunjukkan seberapa tersebar data dari nilai rata-ratanya.
di mana:
- σ adalah simpangan baku
- x adalah setiap nilai data
- μ adalah rata-rata
- N adalah jumlah data
Pentingnya Simpangan Baku
Simpangan baku sangat penting dalam statistik karena:
- Membantu membandingkan kumpulan data yang berbeda
- Digunakan dalam pengujian hipotesis
- Membantu mengidentifikasi outlier (nilai yang sangat berbeda dari data lainnya)
- Memberikan informasi tentang variabilitas data
Rumus Simpangan Baku
Simpangan baku adalah ukuran statistik yang mengukur seberapa tersebar data dari nilai rata-rata. Rumus untuk menghitung simpangan baku populasi (σ) adalah:
σ = √(∑(x – μ)² / N)
di mana:
- x adalah nilai data
- μ adalah nilai rata-rata populasi
- N adalah jumlah data dalam populasi
Rumus untuk menghitung simpangan baku sampel (s) adalah:
s = √(∑(x – x̅)² / (N – 1))
di mana:
- x adalah nilai data
- x̅ adalah nilai rata-rata sampel
- N adalah jumlah data dalam sampel
Perbedaan utama antara rumus simpangan baku populasi dan sampel adalah pada penyebut. Pada rumus populasi, penyebutnya adalah N, sedangkan pada rumus sampel, penyebutnya adalah (N – 1). Hal ini karena dalam praktiknya, kita biasanya tidak mengetahui nilai rata-rata populasi, sehingga kita menggunakan nilai rata-rata sampel sebagai perkiraan.
Cara Menghitung Simpangan Baku: Simpangan Baku Dari Data 6 10 9 7 8 Adalah

Simpangan baku adalah ukuran penyebaran data. Ini mengukur seberapa banyak data menyebar dari nilai rata-ratanya. Simpangan baku yang lebih tinggi menunjukkan penyebaran yang lebih besar.
Langkah-langkah Menghitung Simpangan Baku
- Hitung rata-rata (mean) data.
- Kurangi setiap titik data dari rata-rata untuk mendapatkan deviasi.
- Kuadratkan setiap deviasi.
- Hitung rata-rata kuadrat deviasi (varians).
- Ambil akar kuadrat dari varians untuk mendapatkan simpangan baku.
Contoh
Hitung simpangan baku dari data 6, 10, 9, 7, 8.
Simpangan baku dari data 6, 10, 9, 7, dan 8 adalah 1,41. Lumba-lumba, mamalia laut yang cerdas, dikenal dalam bahasa Inggris sebagai “dolphin”. Deskripsi lumba-lumba dalam bahasa Inggris seringkali mengacu pada karakteristik fisiknya yang unik, seperti moncong panjang dan sirip punggung yang khas.
Kembali pada topik simpangan baku, nilai 1,41 menunjukkan adanya variasi data yang relatif rendah, yang menyiratkan bahwa data tersebut cenderung terpusat di sekitar nilai rata-rata.
- Rata-rata: (6 + 10 + 9 + 7 + 8) / 5 = 8
- Deviasi: 6-8 = -2, 10-8 = 2, 9-8 = 1, 7-8 = -1, 8-8 = 0
- Kuadrat Deviasi: 4, 4, 1, 1, 0
- Varians: (4 + 4 + 1 + 1 + 0) / 5 = 2
- Simpangan Baku: √2 = 1,41
Jadi, simpangan baku dari data yang diberikan adalah 1,41.
Simpangan baku dari data 6 10 9 7 8 adalah 1,64. Dalam seni bela diri karate, gerakan dasar untuk sabuk putih meliputi chudan-tsuki , jodan-tsuki , dan gedan-barai . Simpangan baku yang kecil menunjukkan bahwa data cukup terdistribusi merata di sekitar nilai rata-rata.
Interpretasi Simpangan Baku
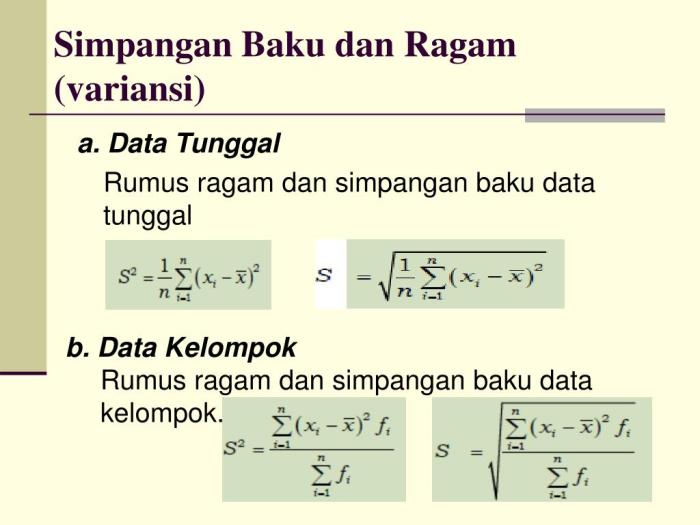
Simpangan baku, dilambangkan dengan σ atau s, adalah ukuran variabilitas data. Ini menunjukkan seberapa tersebar data dari nilai rata-rata.
Simpangan Baku Tinggi
- Menunjukkan bahwa data tersebar luas dari nilai rata-rata.
- Data kurang dapat diprediksi dan memiliki variasi yang lebih besar.
Simpangan Baku Rendah
- Menunjukkan bahwa data berkerumun di sekitar nilai rata-rata.
- Data lebih dapat diprediksi dan memiliki variasi yang lebih kecil.
Aplikasi Simpangan Baku

Simpangan baku merupakan ukuran penyebaran data yang banyak digunakan dalam berbagai bidang untuk mengukur variabilitas dan membuat prediksi.
Ilmu Data
Dalam ilmu data, simpangan baku digunakan untuk:
- Mengidentifikasi pola dan tren dalam data
- Membangun model prediktif
- Mengevaluasi kinerja algoritma
Penelitian Medis
Dalam penelitian medis, simpangan baku digunakan untuk:
- Membandingkan efektivitas perawatan yang berbeda
- Mengidentifikasi faktor risiko penyakit
- Memprediksi hasil pengobatan
Pengendalian Kualitas, Simpangan baku dari data 6 10 9 7 8 adalah
Dalam pengendalian kualitas, simpangan baku digunakan untuk:
- Memantau proses produksi
- Mengidentifikasi variasi yang tidak diinginkan
- Meningkatkan kualitas produk dan layanan
Penutupan
Dengan memahami simpangan baku, kita dapat memperoleh pemahaman yang lebih baik tentang distribusi data, mengidentifikasi pola, dan membuat prediksi yang lebih akurat. Ini adalah alat yang ampuh yang banyak digunakan di berbagai bidang, membantu kita menganalisis data dan mengambil keputusan berdasarkan informasi.
Kumpulan Pertanyaan Umum
Apa rumus simpangan baku?
Simpangan baku populasi: σ = √(Σ(x – μ)² / N)
Simpangan baku sampel: s = √(Σ(x – x̄)² / (N-1))
Bagaimana cara menghitung simpangan baku dari data 6 10 9 7 8?
1. Hitung mean (x̄) = (6 + 10 + 9 + 7 + 8) / 5 = 8
2. Hitung kuadrat deviasi dari mean: (6-8)² = 4, (10-8)² = 4, (9-8)² = 1, (7-8)² = 1, (8-8)² = 0
3. Jumlahkan kuadrat deviasi: 4 + 4 + 1 + 1 + 0 = 10
4. Bagi dengan jumlah data dikurangi 1: 10 / (5-1) = 2,5
5. Ambil akar kuadrat: s = √2,5 = 1,58
