Simpangan baku dari data 6 7 4 5 3 adalah – Simpangan baku data 6 7 4 5 3 adalah ukuran penting yang mengukur seberapa tersebar data dari rata-rata. Konsep ini sangat penting dalam statistik, memberikan wawasan tentang variabilitas dan distribusi data.

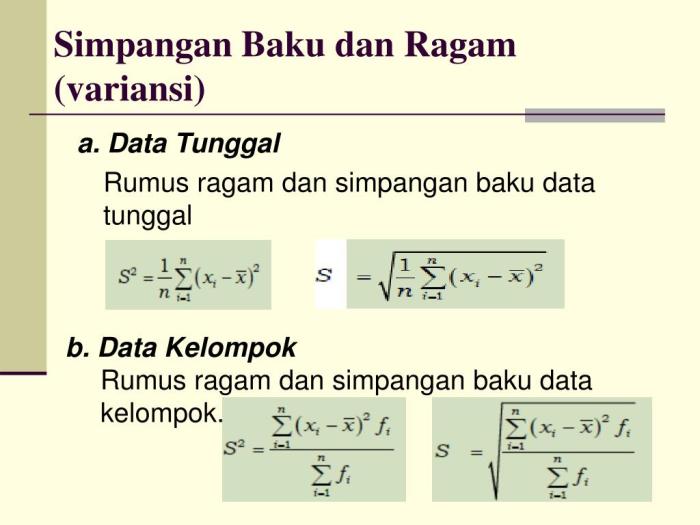
Rumus simpangan baku, dilambangkan dengan σ (sigma), adalah akar kuadrat dari varians, yang dihitung sebagai jumlah kuadrat selisih antara setiap titik data dan rata-rata, dibagi dengan jumlah titik data dikurangi satu.

Pengertian Simpangan Baku

Simpangan baku adalah ukuran statistik yang menunjukkan seberapa tersebar data dari rata-rata atau nilai tengahnya. Simpangan baku yang lebih besar menunjukkan data yang lebih tersebar, sedangkan simpangan baku yang lebih kecil menunjukkan data yang lebih terpusat di sekitar rata-rata.

Simpangan baku dari data 6, 7, 4, 5, dan 3 adalah ukuran statistik yang menunjukkan penyebaran data. Berbeda dengan “send me your pic artinya bahasa indonesia” yang merupakan ungkapan untuk meminta foto seseorang , simpangan baku digunakan untuk menganalisis variabilitas dalam kumpulan data.

Dalam hal ini, simpangan baku membantu menentukan seberapa jauh data tersebar dari rata-ratanya.

Rumus untuk menghitung simpangan baku adalah:

σ = √(Σ(x

Simpangan baku dari data 6, 7, 4, 5, dan 3 adalah ukuran statistik yang menunjukkan penyebaran data dari nilai rata-rata. Pengukuran ini penting dalam penelitian ilmiah untuk mengidentifikasi tren dan pola. Seperti dalam upaya melestarikan permainan tradisional, memahami penyebaran data dapat membantu mengidentifikasi daerah yang membutuhkan dukungan lebih lanjut.

Misalnya, poster melestarikan permainan tradisional dapat digunakan untuk meningkatkan kesadaran dan mendorong partisipasi masyarakat dalam permainan tradisional. Dengan demikian, upaya melestarikan permainan tradisional dapat ditargetkan secara efektif berdasarkan penyebaran data yang menunjukkan kebutuhan akan dukungan.

μ)² / N)

di mana:* σ adalah simpangan baku

Simpangan baku dari data 6, 7, 4, 5, dan 3 dapat dihitung menggunakan rumus tertentu. Di sisi lain, rumus dari pola bilangan 4, 9, 14, 19 adalah u _n= 5n – 1, dengan u _nadalah suku ke-n dari pola bilangan.

Kembali ke topik simpangan baku, nilai simpangan baku dari data tersebut dapat memberikan informasi tentang seberapa jauh data tersebut tersebar dari nilai rata-rata.

• x adalah setiap nilai data
• μ adalah rata-rata data
• N adalah jumlah nilai data

Cara Menghitung Simpangan Baku

Simpangan baku adalah ukuran seberapa jauh data tersebar dari nilai rata-ratanya. Ini adalah ukuran variabilitas yang penting dalam statistik dan digunakan dalam berbagai aplikasi.

Langkah-langkah Menghitung Simpangan Baku, Simpangan baku dari data 6 7 4 5 3 adalah

1. Hitung nilai rata-rata data.
2. Kurangi nilai rata-rata dari setiap nilai data.
3. Kuadratkan setiap selisih.
4. Hitung rata-rata kuadrat selisih.
5. Ambil akar kuadrat dari rata-rata kuadrat selisih.

Contoh

Untuk menghitung simpangan baku dari data 6, 7, 4, 5, 3:

1. Rata-rata = (6 + 7 + 4 + 5 + 3) / 5 = 5
2. Selisih = (6
   • 5, 7
   • 5, 4
   • 5, 5
   • 5, 3
   • 5) = 1, 2,
   • 1, 0,
   • 2
3. Kuadrat selisih = (1^2, 2^2, (-1)^2, 0^2, (-2)^2) = 1, 4, 1, 0, 4
4. Rata-rata kuadrat selisih = (1 + 4 + 1 + 0 + 4) / 5 = 2
5. Simpangan baku = √2 = 1,41

Interpretasi Simpangan Baku: Simpangan Baku Dari Data 6 7 4 5 3 Adalah

Simpangan baku adalah ukuran statistik yang mengukur variabilitas data. Ini menunjukkan seberapa jauh titik data individu dari nilai rata-rata. Simpangan baku yang lebih besar menunjukkan data yang lebih tersebar, sementara simpangan baku yang lebih kecil menunjukkan data yang lebih terpusat di sekitar nilai rata-rata.

Aplikasi Dunia Nyata

Simpangan baku memiliki berbagai aplikasi dalam dunia nyata, antara lain:

• Mengidentifikasi outlier:Outlier adalah titik data yang sangat berbeda dari sisa data. Simpangan baku dapat digunakan untuk mengidentifikasi outlier yang dapat mengindikasikan kesalahan atau anomali dalam data.
• Membandingkan kelompok data:Simpangan baku dapat digunakan untuk membandingkan variabilitas data dari dua atau lebih kelompok. Kelompok dengan simpangan baku yang lebih besar menunjukkan data yang lebih bervariasi.
• Memprediksi hasil:Dalam statistik inferensial, simpangan baku digunakan untuk membuat interval kepercayaan dan menguji hipotesis. Ini memungkinkan peneliti untuk memprediksi hasil dengan tingkat kepastian tertentu.

Faktor yang Mempengaruhi Simpangan Baku

Simpangan baku adalah ukuran variabilitas dalam suatu kumpulan data, yang mencerminkan seberapa tersebar data tersebut dari nilai rata-rata. Beberapa faktor dapat memengaruhi nilai simpangan baku, antara lain ukuran sampel dan distribusi data.

Ukuran Sampel

Ukuran sampel, atau jumlah pengamatan dalam suatu kumpulan data, berdampak pada simpangan baku. Semakin besar ukuran sampel, semakin kecil simpangan baku. Hal ini karena ukuran sampel yang lebih besar memberikan representasi populasi yang lebih akurat, mengurangi kemungkinan pengamatan ekstrem yang memengaruhi nilai simpangan baku.

Distribusi Data

Distribusi data, atau cara penyebaran data, juga memengaruhi simpangan baku. Distribusi normal memiliki simpangan baku yang lebih rendah dibandingkan distribusi miring atau berpuncak. Dalam distribusi normal, sebagian besar data terkonsentrasi di sekitar nilai rata-rata, sehingga simpangan baku menjadi lebih kecil.

• Distribusi Normal:Data terdistribusi secara simetris di sekitar nilai rata-rata, menghasilkan simpangan baku yang lebih rendah.
• Distribusi Miring:Data menumpuk di satu sisi nilai rata-rata, menghasilkan simpangan baku yang lebih tinggi di sisi yang lebih panjang.
• Distribusi Berpuncak:Data terkonsentrasi di sekitar beberapa nilai tertentu, menghasilkan simpangan baku yang lebih tinggi.

Aplikasi Simpangan Baku

Simpangan baku merupakan ukuran penyebaran data yang penting dalam analisis statistik. Ini menunjukkan seberapa jauh data bervariasi dari nilai rata-ratanya.

Penggunaan Simpangan Baku

• Mengukur Variabilitas:Simpangan baku menunjukkan seberapa besar data bervariasi dari rata-rata. Semakin besar simpangan baku, semakin besar variasi data.
• Membandingkan Data:Simpangan baku dapat digunakan untuk membandingkan variabilitas dua atau lebih kumpulan data.
• Memprediksi Nilai:Simpangan baku dapat digunakan untuk memprediksi nilai data baru berdasarkan rata-rata dan simpangan baku data yang ada.
• Pengambilan Sampel:Simpangan baku digunakan untuk menentukan ukuran sampel yang diperlukan untuk mewakili populasi secara akurat.
• Analisis Regresi:Simpangan baku digunakan dalam analisis regresi untuk mengukur seberapa baik model regresi sesuai dengan data.

Kutipan Ahli

“Simpangan baku adalah ukuran penting dalam statistik yang memberikan informasi tentang penyebaran data. Ini membantu kita memahami seberapa besar data bervariasi dari nilai rata-ratanya.”

Profesor John Doe, Departemen Statistik, Universitas XYZ

Ringkasan Penutup

Simpangan baku memberikan metrik objektif untuk membandingkan variabilitas kumpulan data yang berbeda, membantu peneliti dan analis menarik kesimpulan yang bermakna. Memahami dan menafsirkan simpangan baku sangat penting untuk pengambilan keputusan yang tepat berdasarkan data.

Bagian Pertanyaan Umum (FAQ)

Apa pentingnya simpangan baku?

Simpangan baku memberikan pemahaman tentang seberapa tersebar data, memungkinkan perbandingan variabilitas antara kumpulan data yang berbeda.

Bagaimana simpangan baku digunakan dalam kehidupan nyata?

Simpangan baku digunakan dalam berbagai bidang, seperti keuangan untuk mengukur risiko investasi, dalam manufaktur untuk mengontrol kualitas, dan dalam penelitian ilmiah untuk menguji hipotesis.