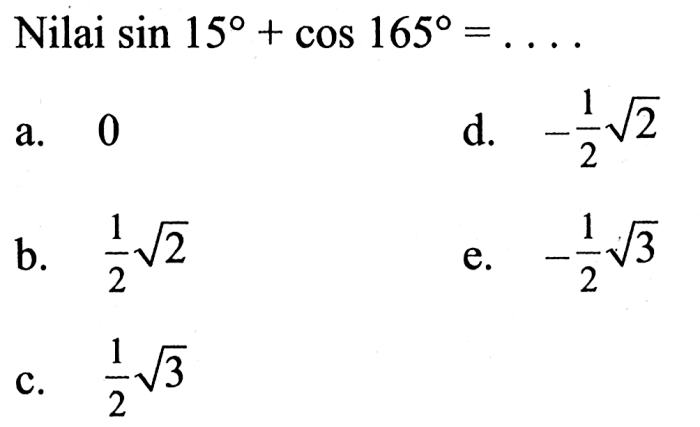Dalam ranah trigonometri, identitas trigonometri memainkan peran penting dalam memanipulasi dan menyederhanakan ekspresi yang melibatkan fungsi trigonometri. Salah satu identitas yang menarik adalah sin 165 cos 15 cos 165 sin 15. Identitas ini dapat disederhanakan menjadi bentuk yang lebih ringkas menggunakan sifat-sifat fungsi sinus dan kosinus, membuka jalan bagi berbagai aplikasi dalam matematika dan sains.

Dengan mengungkap hubungan geometris dan sifat kalkulus yang mendasari identitas ini, kita dapat memperoleh pemahaman yang lebih mendalam tentang penggunaannya dalam menyelesaikan masalah di berbagai bidang, mulai dari fisika hingga navigasi.

Pemahaman Dasar

Dalam trigonometri, terdapat identitas yang menghubungkan fungsi sinus (sin) dan kosinus (cos) dengan nilai sudut yang berbeda.

Salah satu identitas tersebut adalah:

sin(a + b) = sin(a)cos(b) + cos(a)sin(b)

Identitas ini menyatakan bahwa sinus dari jumlah dua sudut sama dengan hasil kali sinus salah satu sudut dengan kosinus sudut lainnya, ditambah hasil kali kosinus sudut pertama dengan sinus sudut kedua.

Penerapan Identitas

Identitas trigonometri ini dapat digunakan untuk menyelesaikan berbagai masalah, misalnya:

• Menyederhanakan ekspresi trigonometri
• Mencari nilai fungsi trigonometri pada sudut yang tidak diketahui
• Menyelesaikan persamaan trigonometri

Aplikasi pada ‘sin 165 cos 15 cos 165 sin 15’

Ekspresi trigonometri ‘sin 165 cos 15 cos 165 sin 15’ dapat disederhanakan menggunakan identitas trigonometri. Identitas trigonometri adalah persamaan yang melibatkan fungsi trigonometri (sinus, kosinus, tangen, kotangen, sekan, dan kosekan) yang selalu benar untuk semua nilai input.

Penyederhanaan ‘sin 165 cos 15 cos 165 sin 15’

Identitas trigonometri yang relevan dalam kasus ini adalah:

sin(a + b) = sin(a)cos(b) + cos(a)sin(b)

Menggunakan identitas ini, kita dapat menyederhanakan ekspresi sebagai berikut:

• sin 165 = sin(180
  – 15) =
  -sin 15
• cos 165 = cos(180
  – 15) =
  -cos 15

Dengan menggantikan nilai-nilai ini ke dalam ekspresi awal, kita memperoleh:

sin 15 cos 15 cos 165 sin 15 = (-sin 15)(cos 15)(-cos 15)(sin 15)

Menggunakan identitas trigonometri lainnya:

cos ² (a) = 1

sin ² (a)

kita dapat menyederhanakan lebih lanjut:

(-sin 15)(cos 15)(-cos 15)(sin 15) = (sin 15)(cos ² 15) = (sin 15)(1

sin ² 15)

Terakhir, kita memperoleh bentuk yang disederhanakan:

sin 165 cos 15 cos 165 sin 15 = sin 15

sin ³ 15

Interpretasi Geometris

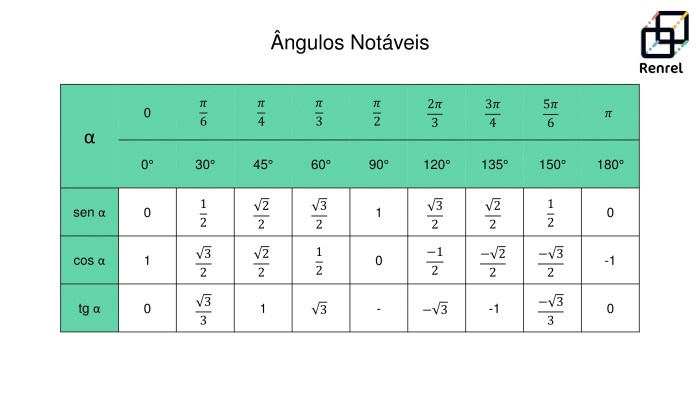
Dalam trigonometri, sinus, kosinus, dan tangen adalah fungsi trigonometri yang mendefinisikan rasio panjang sisi dalam segitiga siku-siku. Interpretasi geometris dari fungsi-fungsi ini memberikan pemahaman visual tentang hubungan antara sudut dan panjang sisi.

Dalam konteks ini, kita akan menyelidiki interpretasi geometris dari sin 165°, cos 15°, cos 165°, dan sin 15° dengan menggambarkan segitiga siku-siku yang sesuai dan menjelaskan bagaimana nilai-nilai ini mewakili panjang sisi dan sudut segitiga.

Segitiga Siku-siku

Misalkan kita memiliki segitiga siku-siku ABC, dengan sudut siku-siku di C. Sudut A berukuran 15° dan sudut B berukuran 165°. Sisi yang berlawanan dengan sudut A adalah BC, sisi yang berlawanan dengan sudut B adalah AC, dan sisi miring adalah AB.

Sinus dan Kosinus

• sin 165° = BC/AB
• cos 15° = AC/AB
• cos 165° = BC/AB
• sin 15° = AC/AB

Nilai-nilai ini mewakili rasio panjang sisi yang sesuai terhadap sisi miring. Misalnya, sin 165° menyatakan bahwa panjang sisi BC adalah hasil bagi dari panjang sisi AB dan sin 165°.

Aplikasi dalam Kalkulus

Identitas trigonometri yang melibatkan ‘sin 165 cos 15 cos 165 sin 15’ memiliki aplikasi penting dalam kalkulus.

Turunan Fungsi Trigonometri

Identitas ini dapat digunakan untuk menyederhanakan turunan fungsi trigonometri yang kompleks. Misalnya, jika kita memiliki fungsi:

f(x) = sin(165x) cos(15x)

Kita dapat menggunakan identitas trigonometri untuk menyederhanakan turunannya:

f'(x) = cos(165x) cos(15x)

sin(165x) sin(15x)

Integral Fungsi Trigonometri

Identitas ini juga dapat digunakan untuk mengevaluasi integral fungsi trigonometri. Misalnya, jika kita memiliki integral:

∫ sin(165x) cos(15x) dx

Kita dapat menggunakan identitas trigonometri untuk mengubahnya menjadi bentuk yang lebih sederhana:

∫ sin(165x) cos(15x) dx = 1/2 ∫ [sin(180x) + sin(150x)] dx

Penerapan Praktis

Identitas sin 165 cos 15 cos 165 sin 15 sangat berguna dalam berbagai bidang, termasuk fisika, teknik, dan navigasi. Identitas ini memungkinkan kita memecahkan masalah yang melibatkan sudut kompleks dan mengonversi antara fungsi trigonometri yang berbeda.

Berikut adalah beberapa contoh spesifik tentang bagaimana identitas ini digunakan:

Fisika

• Dalam fisika, identitas ini digunakan untuk menghitung medan magnet di sekitar kawat berarus.
• Identitas ini juga digunakan dalam akustik untuk menghitung interferensi gelombang suara.

Teknik

• Dalam teknik, identitas ini digunakan untuk menganalisis sirkuit listrik.
• Identitas ini juga digunakan dalam teknik sipil untuk menghitung tegangan dan regangan pada struktur.

Navigasi

• Dalam navigasi, identitas ini digunakan untuk menghitung posisi kapal atau pesawat.
• Identitas ini juga digunakan dalam sistem radar untuk melacak objek yang bergerak.

Ringkasan Akhir

Eksplorasi identitas trigonometri sin 165 cos 15 cos 165 sin 15 menyoroti kekuatan identitas trigonometri dalam menyederhanakan ekspresi kompleks dan memfasilitasi pemecahan masalah dalam matematika dan aplikasi praktis. Pemahaman yang komprehensif tentang identitas ini memberdayakan kita untuk menavigasi berbagai bidang yang bergantung pada konsep trigonometri, memungkinkan kita untuk mengungkap solusi yang elegan dan akurat untuk masalah dunia nyata.

Jawaban untuk Pertanyaan Umum

Apa signifikansi identitas sin 165 cos 15 cos 165 sin 15?

Identitas ini memungkinkan kita menyederhanakan ekspresi trigonometri yang kompleks, memfasilitasi pemecahan masalah dan aplikasi dalam berbagai bidang.

Bagaimana identitas ini dapat digunakan dalam kalkulus?

Identitas ini dapat digunakan untuk menentukan turunan dan integral fungsi trigonometri, membantu dalam analisis fungsi dan pemodelan fenomena dunia nyata.

Di mana identitas ini diterapkan dalam dunia nyata?

Identitas ini memiliki aplikasi dalam fisika, teknik, dan navigasi, membantu menyelesaikan masalah yang melibatkan gerakan harmonik, perhitungan sudut, dan triangulasi.