Barisan geometri merupakan suatu barisan bilangan yang memiliki pola tertentu. Setiap suku dalam barisan geometri diperoleh dengan mengalikan suku sebelumnya dengan suatu bilangan konstan yang disebut rasio. Konsep barisan geometri sangat penting untuk dipahami oleh siswa kelas 10, karena banyak aplikasi dalam kehidupan sehari-hari.

Pada kesempatan ini, kami akan membahas berbagai aspek barisan geometri, mulai dari definisi, sifat-sifat, rumus penjumlahan, hingga penerapannya. Kami juga akan menyediakan beberapa soal latihan untuk menguji pemahaman Anda tentang materi ini.

Definisi Barisan Geometri

Barisan geometri adalah barisan bilangan yang memenuhi sifat suku berikutnya diperoleh dengan mengalikan suku sebelumnya dengan bilangan tetap yang disebut rasio.

Rumus Suku ke-n Barisan Geometri

Rumus suku ke-n barisan geometri diberikan oleh:

$$U_n = a \cdot r^n-1$$

di mana:

• $U_n$ adalah suku ke-n barisan geometri
• $a$ adalah suku pertama barisan geometri
• $r$ adalah rasio barisan geometri
• $n$ adalah nomor urut suku

Sifat-Sifat Barisan Geometri

Barisan geometri memiliki sifat-sifat umum yang membedakannya dari jenis barisan lainnya. Sifat-sifat ini memainkan peran penting dalam memahami dan memanipulasi barisan geometri.

Sifat Umum Barisan Geometri

• Rasio tetap: Setiap suku dalam barisan geometri memiliki rasio yang sama dengan suku sebelumnya. Rasio ini dilambangkan dengan r.
• Suku pertama: Suku pertama dalam barisan geometri dilambangkan dengan a₁.
• Rumus suku ke-n: Suku ke-n dalam barisan geometri dapat ditentukan menggunakan rumus a_n = a₁ x r^n-1, di mana n adalah nomor urut suku.

Sifat Khusus Barisan Geometri dengan Rasio Positif dan Negatif

Selain sifat umum, barisan geometri juga memiliki sifat khusus berdasarkan tanda rasionya:

Rasio Positif (r > 0)

• Konvergen: Barisan geometri dengan rasio positif konvergen ke 0 jika |r| < 1 dan divergen jika |r| > 1.
• Jumlah tak hingga: Jika |r| < 1, jumlah tak hingga dari barisan geometri adalah a₁ / (1
  – r).

Rasio Negatif (r < 0)

• Bolak-balik: Barisan geometri dengan rasio negatif berselang-seling antara positif dan negatif.
• Tidak konvergen: Barisan geometri dengan rasio negatif tidak konvergen.

Rumus Penjumlahan Barisan Geometri

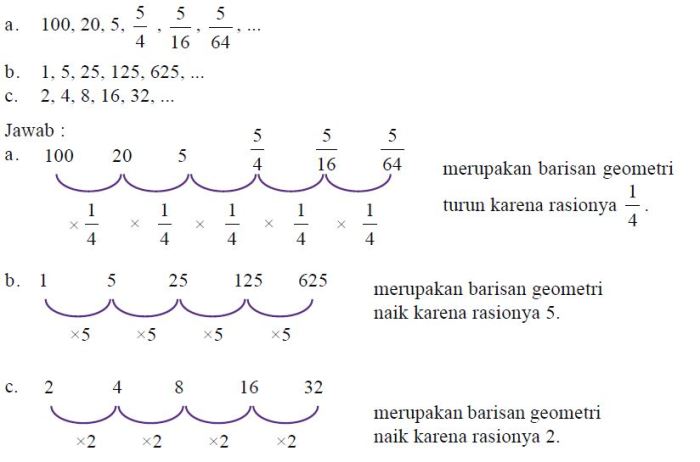
Barisan geometri adalah barisan yang setiap sukunya diperoleh dengan mengalikan suku sebelumnya dengan suatu bilangan tetap yang disebut rasio. Rumus penjumlahan barisan geometri dapat digunakan untuk menentukan jumlah suku-suku tertentu dalam barisan geometri.

Rumus Penjumlahan Barisan Geometri

Untuk n suku pertama dalam barisan geometri dengan suku pertama a dan rasio r, rumus penjumlahannya adalah:$$S_n = \fraca(1

• r^n)1
• r$$

Jika barisan geometri tak hingga dan |r| < 1, maka jumlah suku-sukunya adalah: $$S_\infty = \fraca1 - r$$

Contoh Penggunaan Rumus Penjumlahan Barisan Geometri

Misalkan kita memiliki barisan geometri dengan suku pertama 2 dan rasio 3. Berapakah jumlah 4 suku pertama?Menggunakan rumus penjumlahan barisan geometri:$$S_4 = \frac2(1

• 3^4)1
• 3 = \frac2(1
• 81)-2 = 80$$

Jadi, jumlah 4 suku pertama adalah 80.

Aplikasi Barisan Geometri

Barisan geometri memiliki aplikasi yang luas dalam kehidupan sehari-hari, dari keuangan hingga fisika.

Bidang Keuangan

• Perhitungan Bunga Majemuk: Bunga majemuk adalah bunga yang dihitung tidak hanya dari pokok awal tetapi juga dari bunga yang diperoleh pada periode sebelumnya. Ini dapat dimodelkan menggunakan barisan geometri, di mana suku pertama adalah pokok awal dan rasio umum adalah (1 + suku bunga).
• Peluruhan Nilai Aset: Nilai aset, seperti mobil atau peralatan, cenderung menurun seiring waktu. Proses ini dapat dimodelkan menggunakan barisan geometri, di mana suku pertama adalah nilai awal dan rasio umum adalah nilai depresiasi tahunan.

Bidang Fisika

• Gerak Jatuh Bebas: Ketika sebuah benda jatuh bebas, jarak yang ditempuh dalam setiap detik berturut-turut membentuk barisan geometri, di mana suku pertama adalah jarak yang ditempuh pada detik pertama dan rasio umum adalah percepatan gravitasi.
• Peluruhan Radioaktif: Peluruhan inti atom dapat dimodelkan menggunakan barisan geometri, di mana suku pertama adalah jumlah inti awal dan rasio umum adalah konstanta peluruhan.

Bidang Biologi

• Pertumbuhan Populasi: Pertumbuhan populasi organisme sering mengikuti barisan geometri, di mana suku pertama adalah ukuran populasi awal dan rasio umum adalah laju pertumbuhan.
• Konsentrasi Obat: Setelah obat diberikan, konsentrasinya dalam tubuh menurun seiring waktu. Proses ini dapat dimodelkan menggunakan barisan geometri, di mana suku pertama adalah konsentrasi awal dan rasio umum adalah laju eliminasi.

Soal Latihan Barisan Geometri

Untuk menguji pemahaman siswa tentang barisan geometri, berikut adalah beberapa soal latihan beserta kunci jawaban dan pembahasannya.

Contoh Soal

• Diketahui barisan geometri dengan suku pertama 3 dan suku keempat 48. Tentukan nilai suku keenam barisan tersebut.
• Suatu barisan geometri memiliki rasio 2 dan suku ke-5 adalah 32. Tentukan suku pertama barisan tersebut.
• Sebuah barisan geometri mempunyai jumlah 6 suku pertama 99. Jika suku pertamanya 3, tentukan rasionya.

Kunci Jawaban dan Pembahasan

1. Suku keenam = S ₆ = a ₁ x r ⁵ = 3 x 4 ⁵ = 3 x 1024 = 3072

2. Suku ke-5 = a ₅ = a ₁ x r ⁴ = 32

   Karena r = 2, maka a ₁ = 32 / 2 ⁴ = 32 / 16 = 2

3. Jumlah 6 suku pertama = S ₆ = a ₁ x (1 – r ⁶ ) / (1 – r) = 99

   Dengan a ₁ = 3, maka 99 = 3 x (1 – r ⁶ ) / (1 – r)

   Menyelesaikan persamaan tersebut, diperoleh r = 2

Penutupan

Dengan memahami konsep barisan geometri dengan baik, Anda akan dapat menyelesaikan berbagai soal yang berkaitan dengan topik ini dengan mudah. Soal-soal latihan yang telah kami sediakan akan membantu Anda mengasah keterampilan dalam menyelesaikan masalah yang melibatkan barisan geometri.

Bagian Pertanyaan Umum (FAQ)

Apa yang dimaksud dengan barisan geometri?

Barisan geometri adalah barisan bilangan yang setiap sukunya diperoleh dengan mengalikan suku sebelumnya dengan suatu bilangan konstan yang disebut rasio.

Apa rumus suku ke-n barisan geometri?

Rumus suku ke-n barisan geometri adalah Un = a . r^(n-1), dimana a adalah suku pertama, r adalah rasio, dan n adalah nomor suku.

Apa saja sifat-sifat barisan geometri?

Barisan geometri memiliki sifat-sifat umum, seperti jumlah dua suku berurutan selalu sama dengan hasil kali rasionya, dan jumlah suku pertama hingga suku ke-n selalu sama dengan hasil bagi beda suku pertama dan suku ke-n dibagi dengan beda rasionya.