Dalam fisika, dimensi memegang peran penting dalam memahami dan menganalisis besaran fisik. Dimensi merupakan sifat fundamental yang menentukan karakteristik besaran dan memungkinkan kita mengonversi antar satuan yang berbeda. Artikel ini akan memberikan pemahaman mendalam tentang konsep dimensi fisika, termasuk dimensi besaran pokok dan turunan, analisis dimensi, serta soal dan latihan yang akan mengasah keterampilan siswa dalam topik ini.
Memahami dimensi fisika sangat penting untuk memastikan konsistensi dan validitas dalam perhitungan dan persamaan fisika. Dengan memahami dimensi besaran, kita dapat memeriksa kesesuaian satuan dalam suatu persamaan dan memastikan bahwa hasilnya memiliki dimensi yang tepat. Selain itu, dimensi fisika juga digunakan dalam analisis dimensi, teknik yang ampuh untuk memeriksa kebenaran persamaan fisika dan memperoleh hubungan antara besaran fisik yang berbeda.
Dimensi Fisika
Dimensi fisika adalah konsep penting dalam fisika yang mengacu pada sifat dasar besaran fisika. Setiap besaran fisika memiliki dimensi yang menyatakan jenis besaran dan hubungannya dengan besaran fisika lainnya.
Misalnya, panjang memiliki dimensi [L], waktu memiliki dimensi [T], dan massa memiliki dimensi [M]. Dimensi ini memungkinkan kita untuk mengklasifikasikan dan membandingkan besaran fisika yang berbeda.
Pentingnya Dimensi Fisika dalam Memahami Besaran Fisika
Dimensi fisika sangat penting untuk memahami besaran fisika karena memungkinkan kita untuk:
- Mengidentifikasi jenis besaran fisika
- Membandingkan besaran fisika yang berbeda
- Menghitung dan memprediksi nilai besaran fisika
Mengubah Satuan dengan Memperhatikan Dimensi Fisika
Dimensi fisika juga memainkan peran penting dalam mengubah satuan besaran fisika. Saat mengubah satuan, kita harus memastikan bahwa dimensi kedua satuan tersebut sama. Misalnya, jika kita ingin mengubah 10 meter menjadi sentimeter, kita dapat menggunakan persamaan konversi berikut:
- m = 10 m
- (100 cm / 1 m) = 1000 cm
Dalam persamaan ini, dimensi [L] dari meter dan sentimeter dibatalkan, sehingga memberikan satuan akhir dalam sentimeter.
Dimensi Besaran Pokok
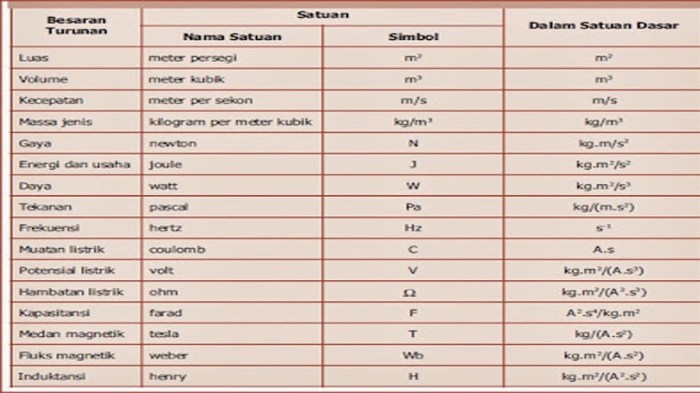
Dimensi besaran pokok adalah besaran dasar yang tidak dapat diturunkan dari besaran lain. Dalam Sistem Internasional (SI), terdapat tujuh besaran pokok, yaitu panjang, massa, waktu, arus listrik, suhu, intensitas cahaya, dan jumlah zat.
Setiap besaran pokok memiliki satuan dasar dan dimensi terkaitnya. Dimensi suatu besaran menyatakan sifat besaran tersebut dan menunjukkan bagaimana besaran tersebut berubah sehubungan dengan besaran pokok lainnya.
Satuan Dasar dan Dimensi Besaran Pokok
| Besaran Pokok | Satuan Dasar | Dimensi |
|---|---|---|
| Panjang | Meter (m) | [L] |
| Massa | Kilogram (kg) | [M] |
| Waktu | Detik (s) | [T] |
| Arus Listrik | Ampere (A) | [I] |
| Suhu | Kelvin (K) | [Θ] |
| Intensitas Cahaya | Candela (cd) | [J] |
| Jumlah Zat | Mol (mol) | [N] |
Contoh penggunaan dimensi besaran pokok dalam persamaan fisika:
Rumus untuk menghitung kecepatan (v) adalah:
v = s / t
Dalam rumus tersebut:
- v adalah kecepatan (m/s)
- s adalah jarak (m)
- t adalah waktu (s)
Dari rumus tersebut, dapat dilihat bahwa dimensi kecepatan adalah [L]/[T].
Dimensi Besaran Turunan

Besaran turunan adalah besaran yang diturunkan dari besaran pokok melalui operasi matematika seperti perkalian, pembagian, pangkat, dan akar. Dimensi besaran turunan dapat diturunkan dari dimensi besaran pokok yang terlibat dalam operasi tersebut.
Menurunkan Dimensi Besaran Turunan
Untuk menurunkan dimensi besaran turunan, ikuti langkah-langkah berikut:
- Tentukan besaran pokok yang terlibat dalam operasi.
- Tuliskan dimensi besaran pokok tersebut menggunakan simbol dimensi yang sesuai.
- Terapkan operasi matematika yang digunakan untuk menurunkan besaran turunan ke dimensi besaran pokok.
- Hasilnya adalah dimensi besaran turunan.
Rumus Dimensi Besaran Turunan
Dimensi besaran turunan dapat dihitung menggunakan rumus berikut:
$$[A] = [B]^a [C]^b [D]^c …$$
di mana:
- $[A]$ adalah dimensi besaran turunan
- $[B], [C], [D], …$ adalah dimensi besaran pokok yang terlibat
- $a, b, c, …$ adalah eksponen yang sesuai dengan besaran pokok
Analisis Dimensi
Analisis dimensi adalah teknik penting dalam fisika yang digunakan untuk memeriksa konsistensi persamaan dan memecahkan masalah. Teknik ini didasarkan pada prinsip bahwa besaran fisika dapat dinyatakan dalam istilah dimensi dasarnya, seperti panjang, massa, dan waktu.
Analisis dimensi melibatkan dua langkah utama:
- Identifikasi Dimensi: Tentukan dimensi setiap besaran dalam persamaan atau masalah menggunakan satuan SI.
- Bandingkan Dimensi: Bandingkan dimensi sisi kiri dan kanan persamaan. Jika kedua sisi memiliki dimensi yang sama, maka persamaan tersebut secara dimensi benar.
Kegunaan Analisis Dimensi
- Memeriksa Konsistensi Persamaan: Analisis dimensi dapat digunakan untuk memeriksa apakah persamaan fisika secara dimensi benar, meskipun nilai numeriknya belum diketahui.
- Mengidentifikasi Kesalahan: Jika kedua sisi persamaan memiliki dimensi yang berbeda, ini menunjukkan adanya kesalahan dalam persamaan atau kesalahan konseptual dalam masalah.
- Menyelesaikan Masalah Fisika: Analisis dimensi dapat digunakan untuk menyelesaikan masalah fisika dengan menemukan hubungan antara besaran yang tidak diketahui.
Contoh Penggunaan Analisis Dimensi
Misalkan kita memiliki persamaan berikut:
v = u + at
Dimana:
- v adalah kecepatan akhir
- u adalah kecepatan awal
- a adalah percepatan
- t adalah waktu
Menggunakan analisis dimensi, kita dapat memeriksa apakah persamaan ini secara dimensi benar:
| Besaran | Dimensi (SI) | Sisi Kiri | Sisi Kanan |
|---|---|---|---|
| Kecepatan | [L T-1] | v | u + at |
| Percepatan | [L T-2] | – | a |
| Waktu | [T] | – | t |
Seperti yang dapat kita lihat, dimensi kedua sisi persamaan adalah [L T -1 ], sehingga persamaan tersebut secara dimensi benar.
Soal dan Latihan
Soal dan latihan berikut dirancang untuk membantu siswa mengasah pemahaman mereka tentang dimensi fisika.
Menentukan Dimensi Besaran Fisika
- Tentukan dimensi besaran berikut: percepatan, gaya, energi, momentum, dan tekanan.
Konversi Satuan Menggunakan Dimensi Fisika
- Konversikan 500 Newton menjadi dyne menggunakan dimensi fisika.
- Ubah 100 joule menjadi erg menggunakan dimensi fisika.
Menganalisis Dimensi Persamaan Fisika
- Analisis dimensi persamaan F = ma dan periksa apakah persamaan tersebut memiliki dimensi yang sama di kedua sisi.
- Tunjukkan bahwa dimensi persamaan E = mc² adalah sama di kedua sisi.
Ringkasan Penutup

Soal dimensi fisika merupakan bagian integral dari kurikulum fisika kelas 10. Dengan mempelajari topik ini, siswa akan memperoleh pemahaman yang kuat tentang sifat dasar besaran fisika dan pentingnya dimensi dalam perhitungan dan analisis fisika. Soal dan latihan yang disajikan dalam artikel ini akan membantu siswa menguasai konsep dimensi fisika dan menerapkannya dalam berbagai situasi.
Ringkasan FAQ
Apa yang dimaksud dengan dimensi fisika?
Dimensi fisika adalah sifat fundamental yang menggambarkan jenis besaran fisik, seperti panjang, massa, atau waktu.
Mengapa dimensi fisika penting?
Dimensi fisika memastikan konsistensi satuan dalam perhitungan dan persamaan fisika, serta memungkinkan konversi antar satuan yang berbeda.
Bagaimana cara mengubah satuan dengan memperhatikan dimensi fisika?
Untuk mengubah satuan, kalikan besaran dengan faktor konversi yang memiliki dimensi yang sama tetapi satuan yang berbeda.
Apa yang dimaksud dengan besaran turunan?
Besaran turunan adalah besaran yang diturunkan dari besaran pokok, seperti kecepatan, percepatan, atau gaya.
Bagaimana cara menganalisis dimensi persamaan fisika?
Analisis dimensi melibatkan pemeriksaan dimensi kedua sisi persamaan untuk memastikan bahwa dimensi kedua sisi sama.
