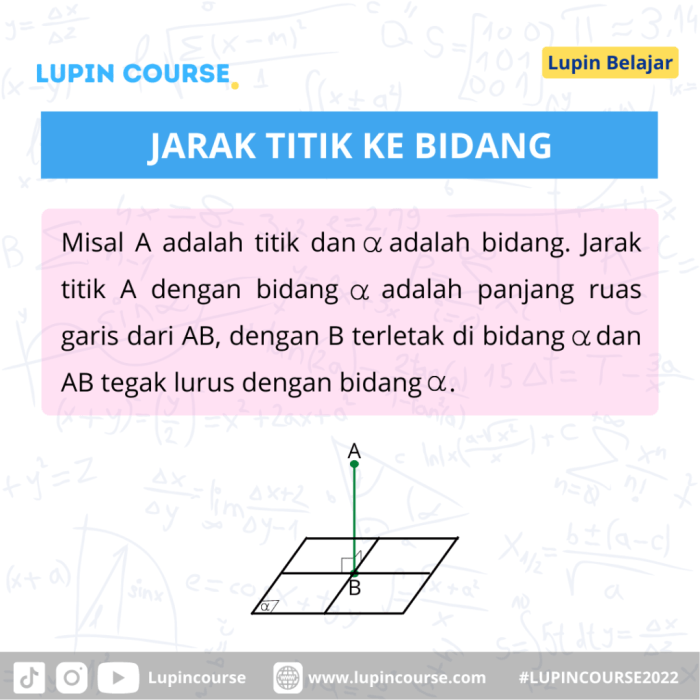
Dalam geometri, memahami jarak antara garis dan bidang sangat penting untuk menyelesaikan berbagai masalah. Konsep ini memiliki aplikasi luas dalam bidang teknik, arsitektur, dan fisika.

Artikel ini akan memberikan penjelasan komprehensif tentang soal jarak garis ke bidang, termasuk rumus umum, langkah-langkah perhitungan, dan penerapannya dalam konteks geometri.

Pengertian Jarak Garis ke Bidang

Jarak garis ke bidang adalah jarak tegak lurus dari suatu titik pada garis ke bidang. Jarak ini diukur dari titik terdekat pada garis ke bidang.

Rumus umum untuk menghitung jarak garis ke bidang adalah:

$$d = \frac|ax_0 + by_0 + cz_0 + d|\sqrta^2 + b^2 + c^2$$

di mana:* \(d\) adalah jarak garis ke bidang

• \(a, b, c\) adalah koefisien persamaan bidang
• \(x_0, y_0, z_0\) adalah koordinat titik pada garis
• \(d\) adalah konstanta persamaan bidang

Cara Menghitung Jarak Garis ke Bidang

Untuk menghitung jarak garis ke bidang, diperlukan persamaan garis dan persamaan bidang. Persamaan garis dapat ditulis sebagai:

x = x ₀ + at, y = y ₀ + bt, z = z ₀ + ct

dengan (x ₀ , y ₀ , z ₀ ) sebagai titik pada garis dan (a, b, c) sebagai vektor arah garis. Persamaan bidang dapat ditulis sebagai:

Ax + By + Cz + D = 0

dengan A, B, C, dan D sebagai konstanta.

Langkah-langkah Menghitung Jarak

1. Tentukan titik P pada garis yang paling dekat dengan bidang.
2. Hitung vektor normal bidang, n = (A, B, C).
3. Hitung vektor arah garis, v = (a, b, c).
4. Hitung jarak dari titik P ke bidang menggunakan rumus:

   d = | n · ( r _P

   r ₀ )| / | n |

   dengan r _P = (x _P , y _P , z _P ) sebagai koordinat titik P dan r ₀ = (x ₀ , y ₀ , z ₀ ) sebagai titik pada bidang.

Contoh Perhitungan

Misalkan kita memiliki garis dengan persamaan x = 1 + t, y = 2 – t, z = 3 + 2t dan bidang dengan persamaan x + 2y – z = 1. Tentukan jarak garis ke bidang.

1. Titik pada garis: (1, 2, 3)

2. Vektor normal bidang: n = (1, 2, -1)

3. Vektor arah garis: v = (1, -1, 2)

4. Jarak garis ke bidang:

d = | n · ( r _P

r ₀ )| / | n |

= |(1, 2,

• 1) · (1, 2, 3)
• (1, 2, 1)| / |(1, 2,
• 1)|

= |(1, 2, 3)

(1, 2, 1)| / √(1 ² + 2 ² + (-1) ² )

= |(0, 0, 2)| / √6= 2 / √6≈ 0,82

Prosedur Menggunakan Rumus Jarak Garis ke Bidang

Rumus jarak garis ke bidang digunakan untuk menghitung jarak terpendek antara garis dan bidang dalam ruang tiga dimensi. Rumus umum yang digunakan adalah:

$$d = \frac|ax_0 + by_0 + cz_0 + d|\sqrta^2 + b^2 + c^2$$

di mana:

• $(a, b, c)$ adalah vektor normal bidang
• $(x_0, y_0, z_0)$ adalah titik pada bidang
• $d$ adalah jarak dari titik asal ke bidang
• $d$ adalah jarak garis ke bidang

Dalam kasus khusus, rumus jarak garis ke bidang dapat disederhanakan sebagai berikut:

Garis Sejajar Bidang

Jika garis sejajar dengan bidang, maka jarak garis ke bidang sama dengan jarak dari titik asal ke bidang. Rumus yang digunakan adalah:

$$d = \frac|d|\sqrta^2 + b^2 + c^2$$

Garis Tegak Lurus Bidang

Jika garis tegak lurus dengan bidang, maka jarak garis ke bidang sama dengan jarak dari titik pada garis ke bidang. Rumus yang digunakan adalah:

$$d = \frac|ax_1 + by_1 + cz_1 + d|\sqrta^2 + b^2 + c^2$$

di mana $(x_1, y_1, z_1)$ adalah titik pada garis.

Aplikasi Jarak Garis ke Bidang dalam Geometri

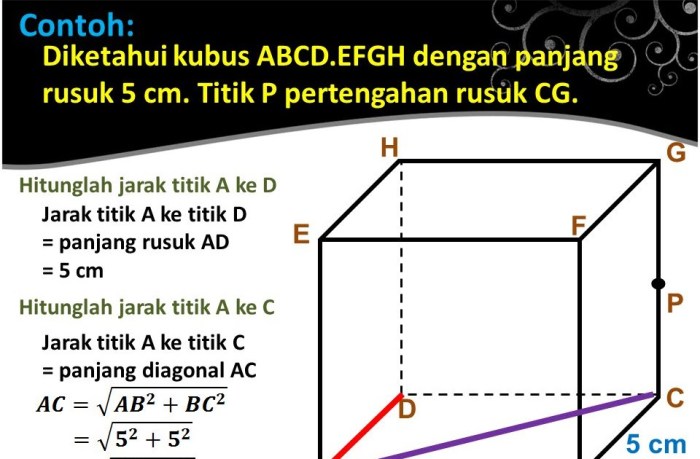
Konsep jarak garis ke bidang memiliki berbagai aplikasi penting dalam menyelesaikan masalah geometri. Berikut adalah beberapa contohnya:

Mencari Jarak Titik ke Bidang

Diketahui sebuah titik dan sebuah bidang, jarak dari titik ke bidang dapat ditentukan menggunakan rumus jarak garis ke bidang. Rumus ini berguna dalam berbagai aplikasi, seperti menentukan jarak dari titik ke permukaan benda atau menghitung jarak antara dua benda yang tidak sejajar.

Menentukan Apakah Dua Garis Sejajar atau Tegak Lurus

Dengan menggunakan jarak garis ke bidang, kita dapat menentukan apakah dua garis sejajar atau tegak lurus. Jika jarak antara kedua garis sama dengan nol, maka garis-garis tersebut sejajar. Jika jaraknya tidak sama dengan nol, maka garis-garis tersebut tegak lurus.

Contoh Soal Jarak Garis ke Bidang

Berikut adalah beberapa contoh soal yang berkaitan dengan jarak garis ke bidang:

Soal 1

Tentukan jarak antara garis ℓ dengan persamaan parametrik \mathbfr(t) = (1+t)\mathbfi + (2-t)\mathbfj + 3\mathbfk dan bidang Π dengan persamaan x + 2y – 3z = 6 .

Solusi:

• Tentukan vektor arah garis ℓ: \mathbfv = \mathbfi
  – \mathbfj.
• Tentukan titik pada bidang Π: (0, 0, 2).
• Gunakan rumus jarak garis ke bidang: d = \frac|\mathbfv\cdot(\mathbfb
  – \mathbfa)|\|\mathbfv\| , di mana \mathbfa adalah titik pada garis, \mathbfb adalah titik pada bidang, dan \mathbfv adalah vektor arah garis.
• Substitusikan nilai yang diketahui: d = \frac|(1+0)
  – (2-0)|\sqrt1^2 + (-1)^2 = \frac3\sqrt2 = \sqrt\frac182 \approx 4,24.

Soal 2

Tentukan jarak antara garis ℓ dengan persamaan vektor \mathbfr(t) = (2, 1, -1) + t(1, 2, 3) dan bidang Π dengan persamaan 2x – y + 3z = 5 .

Solusi:

• Tentukan vektor arah garis ℓ: \mathbfv = (1, 2, 3).
• Tentukan titik pada bidang Π: (0, 5, 0).
• Gunakan rumus jarak garis ke bidang:
• Substitusikan nilai yang diketahui: d = \frac|(2-0)
  – (1-5) + (3-0)|\sqrt1^2 + 2^2 + 3^2 = \frac10\sqrt14 \approx 2,83.

Ilustrasi Geometris Jarak Garis ke Bidang

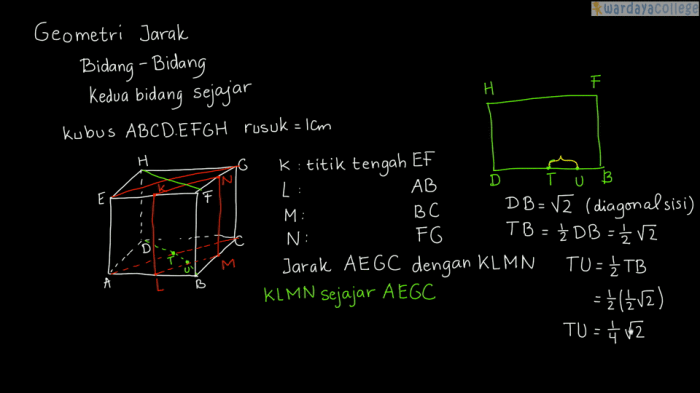
Ilustrasi geometris dapat membantu memvisualisasikan konsep jarak garis ke bidang. Berikut ini adalah gambarannya:

Misalkan kita memiliki garis yang sejajar dengan bidang dan sebuah titik pada garis tersebut. Jarak dari titik ke bidang adalah jarak terpendek dari titik ke bidang, yang tegak lurus dengan bidang. Jarak ini dapat dilambangkan dengan d.

Elemen yang Terlibat

• Garis: garis yang sejajar dengan bidang
• Bidang: bidang yang sejajar dengan garis
• Titik: titik pada garis
• Jarak (d): jarak terpendek dari titik ke bidang, tegak lurus dengan bidang

Interpretasi Fisik Jarak Garis ke Bidang

Jarak garis ke bidang memiliki interpretasi fisik yang signifikan dalam berbagai aplikasi praktis, seperti arsitektur dan teknik.

Dalam arsitektur, jarak garis ke bidang dapat mewakili:

• Jarak antara dinding dan furnitur, memastikan ada ruang yang cukup untuk bergerak dan mencegah benturan.
• Jarak antara langit-langit dan lampu gantung, memastikan pencahayaan yang optimal dan mencegah bahaya tersandung.
• Jarak antara kolom dan dinding, menentukan stabilitas struktural bangunan.

Dalam teknik, jarak garis ke bidang dapat mewakili:

• Jarak antara pipa dan dinding, memastikan pipa tidak menghalangi akses atau menyebabkan kerusakan.
• Jarak antara kabel dan langit-langit, mencegah bahaya tersengat listrik dan memastikan kabel terpasang dengan benar.
• Jarak antara poros dan bantalan, menentukan kinerja dan umur peralatan.

Ringkasan Akhir

Dengan memahami soal jarak garis ke bidang, kita dapat menyelesaikan masalah geometri yang kompleks, menentukan hubungan antara garis dan bidang, dan membuat interpretasi fisik yang bermakna.

Tanya Jawab (Q&A)

Apa itu jarak garis ke bidang?

Jarak garis ke bidang adalah jarak terpendek antara titik mana pun pada garis ke bidang.

Bagaimana cara menghitung jarak garis ke bidang?

Jarak garis ke bidang dapat dihitung menggunakan rumus umum: jarak = |(a ₁ x + b ₁ y + c ₁ z + d ₁ ) / √(a ₂ ² + b ₂ ² + c ₂ ² )|, di mana (a ₁ , b ₁ , c ₁ , d ₁ ) adalah koefisien bidang dan (a ₂ , b ₂ , c ₂ ) adalah vektor arah garis.