Dalam statistik, modus, median, dan mean merupakan ukuran tendensi sentral yang penting untuk menganalisis dan memahami kumpulan data. Masing-masing ukuran ini memiliki pengertian, metode perhitungan, dan kegunaan yang berbeda dalam berbagai situasi.

Artikel ini akan membahas secara mendalam tentang modus, median, dan mean, serta menyajikan soal-soal latihan untuk menguji pemahaman siswa kelas 6 tentang konsep-konsep ini.

Pengertian Modus, Median, dan Mean

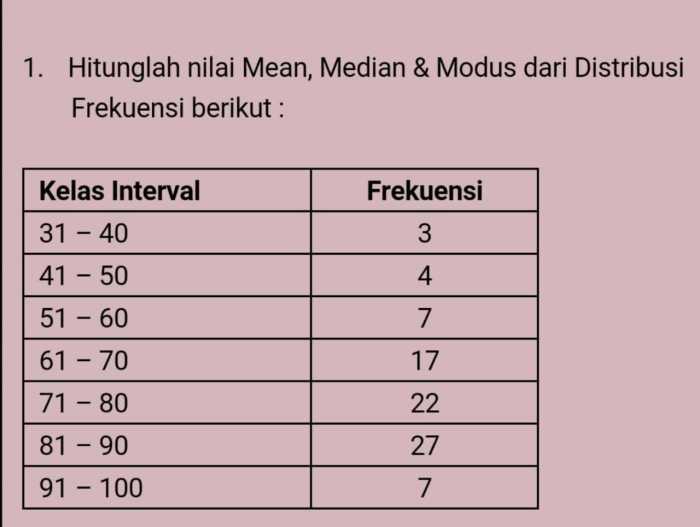
Dalam statistika, modus, median, dan mean adalah tiga ukuran yang digunakan untuk mendeskripsikan pusat suatu kumpulan data.

Modus

Modus adalah nilai yang paling sering muncul dalam suatu kumpulan data. Modus dapat memberikan gambaran tentang nilai yang paling umum atau representatif dalam data.

Median

Median adalah nilai tengah dari suatu kumpulan data yang telah diurutkan dari nilai terkecil ke terbesar. Median membagi data menjadi dua bagian yang sama, di mana setengah dari data berada di bawah median dan setengahnya lagi berada di atas median.

Mean

Mean adalah nilai rata-rata dari seluruh data dalam suatu kumpulan data. Mean dihitung dengan menjumlahkan semua nilai data dan kemudian membaginya dengan jumlah data.

Cara Menghitung Modus, Median, dan Mean

Dalam statistika, ukuran tendensi sentral digunakan untuk menggambarkan data yang telah dikumpulkan. Tiga ukuran tendensi sentral yang umum digunakan adalah modus, median, dan mean. Berikut adalah cara menghitung masing-masing ukuran:

Modus

Modus adalah nilai yang paling sering muncul dalam suatu kumpulan data. Untuk menghitung modus, cukup identifikasi nilai yang paling sering muncul.

Median

Median adalah nilai tengah dalam suatu kumpulan data ketika data diurutkan dari yang terkecil ke terbesar. Jika jumlah data ganjil, maka median adalah nilai tengah. Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengah.

Mean

Mean adalah rata-rata dari semua nilai dalam suatu kumpulan data. Untuk menghitung mean, jumlahkan semua nilai dan bagi dengan jumlah data.

Contoh Perhitungan

Misalkan kita memiliki kumpulan data berikut: 5, 7, 9, 11, 13, 15, 17.

• Modus: 11 dan 13 (keduanya muncul dua kali, paling sering)
• Median: 11 (nilai tengah ketika data diurutkan)
• Mean: (5 + 7 + 9 + 11 + 13 + 15 + 17) / 7 = 11 (rata-rata semua nilai)

Perbedaan Modus, Median, dan Mean

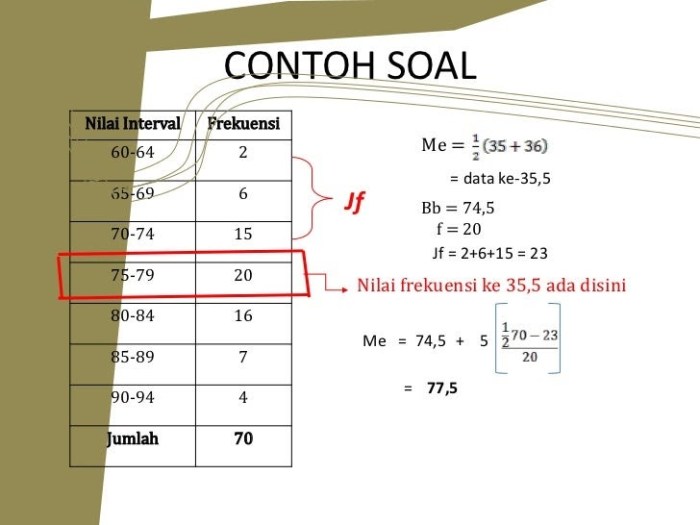
Dalam statistika, modus, median, dan mean adalah tiga ukuran tendensi sentral yang digunakan untuk mendeskripsikan distribusi data. Ketiganya memiliki karakteristik dan kegunaan yang berbeda.

Tabel Perbandingan Modus, Median, dan Mean

Ukuran Tendensi Sentral	Definisi	Kelebihan	Kekurangan
Modus	Nilai yang paling sering muncul dalam suatu kumpulan data.	Mudah dihitung, cocok untuk data kualitatif.	Tidak menggambarkan data secara keseluruhan, dapat berubah drastis dengan penambahan atau pengurangan data.
Median	Nilai tengah dalam suatu kumpulan data yang telah diurutkan.	Tidak terpengaruh oleh nilai ekstrem, cocok untuk data yang miring.	Tidak mudah dihitung untuk kumpulan data yang besar, tidak memberikan informasi tentang penyebaran data.
Mean	Jumlah semua nilai dalam suatu kumpulan data dibagi dengan jumlah data.	Menggambarkan data secara keseluruhan, mudah dihitung.	Dapat terpengaruh oleh nilai ekstrem, tidak cocok untuk data yang miring.

Kelebihan dan Kekurangan Masing-Masing Ukuran Tendensi Sentral

Setiap ukuran tendensi sentral memiliki kelebihan dan kekurangannya masing-masing. Modus cocok untuk data kualitatif atau data dengan nilai yang berulang. Median cocok untuk data yang miring atau memiliki nilai ekstrem. Mean cocok untuk data yang simetris dan tidak memiliki nilai ekstrem.

Pemilihan ukuran tendensi sentral yang tepat bergantung pada sifat data dan tujuan analisis. Dengan memahami perbedaan dan kelebihan serta kekurangan masing-masing ukuran, peneliti dapat memilih ukuran yang paling sesuai untuk menggambarkan data mereka secara akurat.

Penerapan Modus, Median, dan Mean

Modus, median, dan mean merupakan ukuran statistik yang digunakan untuk mendeskripsikan kumpulan data. Masing-masing ukuran ini memiliki tujuan dan penggunaan tertentu.

Modus

Modus adalah nilai yang paling sering muncul dalam suatu kumpulan data. Modus dapat digunakan untuk menentukan pilihan yang paling populer atau umum. Misalnya, jika sebuah survei menanyakan makanan favorit orang, dan pizza adalah pilihan yang paling banyak dipilih, maka pizza adalah modus dari kumpulan data tersebut.

Median

Median adalah nilai tengah suatu kumpulan data ketika data tersebut diurutkan dari yang terkecil hingga terbesar. Median mewakili nilai yang membagi kumpulan data menjadi dua bagian yang sama. Median dapat digunakan untuk mengidentifikasi nilai yang lebih representatif dari kumpulan data, terutama ketika data tersebut mengandung nilai ekstrem atau outlier.

Mean

Mean, juga dikenal sebagai rata-rata, adalah jumlah semua nilai dalam suatu kumpulan data dibagi dengan jumlah data tersebut. Mean dapat digunakan untuk menghitung nilai rata-rata suatu kumpulan data. Mean sangat dipengaruhi oleh nilai ekstrem, sehingga tidak selalu menjadi representasi terbaik dari kumpulan data.

Latihan Soal Modus, Median, dan Mean

Untuk menguji pemahaman siswa tentang modus, median, dan mean, berikut beberapa soal latihan:

Soal Latihan

• Tentukan modus, median, dan mean dari data berikut: 5, 7, 9, 11, 11, 13, 15
• Sebuah toko buku memiliki penjualan buku selama seminggu sebagai berikut: 25, 30, 35, 40, 45, 50. Hitunglah modus, median, dan mean penjualan buku tersebut.
• Nilai ulangan matematika dari 10 siswa adalah: 75, 80, 85, 90, 95, 100, 105, 110, 115, 120. Tentukan modus, median, dan mean nilai ulangan tersebut.

Kunci Jawaban

• Modus: 11, Median: 11, Mean: 10
• Modus: Tidak ada (tidak ada nilai yang muncul paling sering), Median: 40, Mean: 38
• Modus: 110, Median: 105, Mean: 100

Kesimpulan Akhir

Dengan memahami konsep modus, median, dan mean, siswa dapat menganalisis data secara efektif, membuat prediksi, dan mengambil keputusan yang tepat. Ukuran-ukuran tendensi sentral ini memainkan peran penting dalam berbagai bidang, seperti sains, bisnis, dan kehidupan sehari-hari.

Jawaban untuk Pertanyaan Umum

Apa itu jangkauan data?

Jangkauan data adalah selisih antara nilai terbesar dan nilai terkecil dalam suatu kumpulan data.

Bagaimana cara menghitung simpangan rata-rata?

Simpangan rata-rata dihitung dengan menjumlahkan selisih setiap data dengan mean, kemudian dibagi dengan jumlah data.

Apa kelebihan menggunakan median dibandingkan mean?

Median tidak terpengaruh oleh nilai ekstrem, sehingga lebih mewakili nilai tengah data dibandingkan mean.