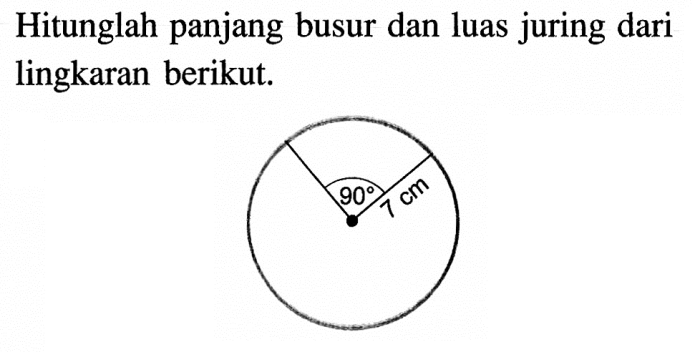
Dalam geometri, konsep panjang busur dan luas juring memainkan peran penting dalam memahami bentuk dan ukuran lingkaran. Artikel ini akan mengeksplorasi definisi, rumus, metode perhitungan, dan aplikasi praktis dari konsep-konsep ini.

Panjang busur mengacu pada jarak di sepanjang tepi lingkaran, sedangkan luas juring mengacu pada area yang dibatasi oleh busur dan dua jari-jari yang menghubungkannya ke pusat lingkaran. Memahami konsep-konsep ini sangat penting untuk menyelesaikan soal-soal geometri dan memiliki aplikasi dalam berbagai bidang kehidupan.

Pengertian dan Rumus

Dalam geometri, panjang busur adalah panjang bagian lengkung lingkaran, sedangkan luas juring adalah luas daerah yang dibatasi oleh dua jari-jari dan busur lingkaran.

Rumus Panjang Busur

Rumus untuk menghitung panjang busur (s) adalah:

s = rθ

di mana:

• r adalah jari-jari lingkaran
• θ adalah sudut pusat yang mengapit busur (dalam radian)

Rumus Luas Juring

Rumus untuk menghitung luas juring (A) adalah:

A = (1/2)r²θ

di mana:

• r adalah jari-jari lingkaran
• θ adalah sudut pusat yang mengapit juring (dalam radian)

Cara Menghitung

Panjang Busur

Untuk menghitung panjang busur, ikuti langkah-langkah berikut:

• Ukur jari-jari lingkaran (r).
• Ukur sudut pusat yang membentuk busur (θ), dalam radian.
• Gunakan rumus berikut: Panjang Busur = r
  – θ

Luas Juring

Untuk menghitung luas juring, ikuti langkah-langkah berikut:

• Ukur jari-jari lingkaran (r).
• Ukur sudut pusat yang membentuk juring (θ), dalam radian.
• Gunakan rumus berikut: Luas Juring = (1/2)
  – r²
  – θ

Contoh Soal dan Pembahasan

Untuk memahami konsep panjang busur dan luas juring, berikut beberapa contoh soal beserta pembahasannya:

Soal 1

Sebuah lingkaran memiliki jari-jari 10 cm. Hitunglah panjang busur lingkaran yang memiliki sudut pusat 60°.

Pembahasan:

• Rumus panjang busur: s = rθ, dimana r adalah jari-jari dan θ adalah sudut pusat dalam radian.
• Konversikan 60° ke radian: θ = 60° x (π/180°) = π/3 radian.
• Substitusikan nilai r dan θ ke dalam rumus: s = 10 cm x (π/3) = 10π/3 cm ≈ 10,47 cm.

Soal 2

Sebuah juring lingkaran memiliki panjang busur 15 cm dan sudut pusat 120°. Hitunglah luas juring tersebut.

Pembahasan:

• Rumus luas juring: A = (1/2)rsθ, dimana r adalah jari-jari, s adalah panjang busur, dan θ adalah sudut pusat dalam radian.
• Karena panjang busur dan sudut pusat sudah diketahui, kita dapat mencari jari-jari (r) dengan mengisolasi r dari rumus panjang busur: r = s/θ.
• Substitusikan nilai s dan θ ke dalam rumus untuk mencari r: r = 15 cm / (120° x (π/180°)) = 15 cm / (2π/3) ≈ 7,5 cm.
• Substitusikan nilai r, s, dan θ ke dalam rumus luas juring: A = (1/2) x 7,5 cm x 15 cm x (120° x (π/180°)) ≈ 84,82 cm².

Penerapan dalam Kehidupan Nyata

Konsep panjang busur dan luas juring memiliki aplikasi luas dalam kehidupan sehari-hari, mulai dari arsitektur hingga teknik.

Arsitektur

• Mendesain lengkungan dan kubah pada bangunan: Panjang busur membantu menentukan bentuk dan ukuran lengkungan, sementara luas juring menentukan luas permukaan yang akan ditutupi.
• Menghitung luas jendela dan pintu melengkung: Panjang busur dan luas juring digunakan untuk menentukan luas kaca yang dibutuhkan untuk mengisi bukaan melengkung.

Teknik

• Merancang roda gigi dan katrol: Panjang busur membantu menentukan jumlah gigi pada roda gigi, sementara luas juring menentukan kekuatan dan efisiensi katrol.
• Membuat jembatan dan struktur melengkung: Konsep ini digunakan untuk menghitung beban dan tegangan pada struktur melengkung, memastikan stabilitas dan keamanannya.

Manfaat Memahami Konsep Ini

Memahami panjang busur dan luas juring sangat penting karena:

• Memungkinkan perhitungan akurat dalam desain dan konstruksi.
• Meningkatkan efisiensi dalam penggunaan bahan dan sumber daya.
• Membantu dalam memahami prinsip-prinsip mekanika dan teknik.
• Meningkatkan pemahaman tentang geometri dan aplikasinya dalam dunia nyata.

Ilustrasi dan Visualisasi

Bagian ini menyajikan ilustrasi dan visualisasi yang membantu memahami konsep panjang busur dan luas juring.

Berikut tabel yang menunjukkan hubungan antara panjang busur, luas juring, dan jari-jari lingkaran:

Panjang Busur	Luas Juring	Jari-jari Lingkaran
$s\; =\; r\backslash theta$	$A\; =\; \backslash frac12r^2\backslash theta$	$r$

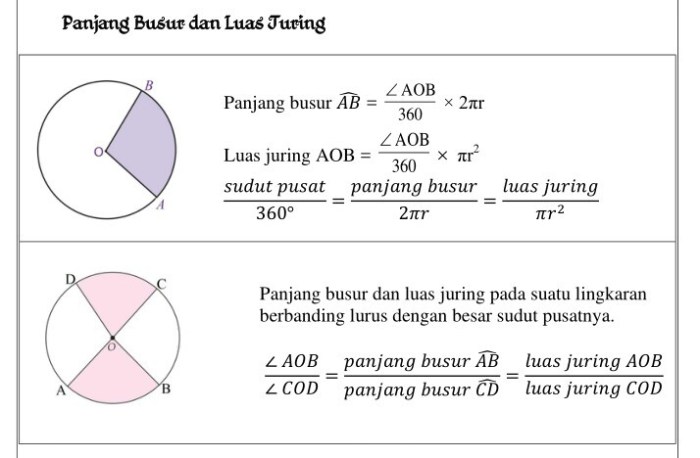
Ilustrasi Konsep

Ilustrasi berikut menggambarkan konsep panjang busur dan luas juring pada lingkaran:

Bayangkan sebuah lingkaran dengan pusat $O$ dan jari-jari $r$ . Misalkan kita mengambil dua titik pada lingkaran, $A$ dan $B$ , yang membentuk busur $AB$ . Sudut pusat yang dibentuk oleh $OA$ dan $OB$ dilambangkan dengan $\backslash theta$ .

Panjang busur $AB$ adalah jarak sepanjang busur tersebut, yang dihitung menggunakan rumus $s\; =\; r\backslash theta$ , di mana $r$ adalah jari-jari lingkaran dan $\backslash theta$ adalah sudut pusat dalam radian.

Luas juring yang dibatasi oleh busur $AB$ dan dua jari-jari $OA$ dan $OB$ adalah $A\; =\; \backslash frac12r^2\backslash theta$ , di mana $r$ adalah jari-jari lingkaran dan $\backslash theta$ adalah sudut pusat dalam radian.

Ringkasan Terakhir

Dengan memahami panjang busur dan luas juring, individu dapat memperoleh wawasan tentang sifat lingkaran dan menyelesaikan masalah geometri yang kompleks. Konsep-konsep ini tidak hanya bermanfaat secara akademis tetapi juga memiliki aplikasi praktis yang luas, seperti dalam arsitektur, teknik, dan desain.

Pertanyaan Umum (FAQ)

Apa perbedaan antara panjang busur dan luas juring?

Panjang busur adalah jarak di sepanjang tepi lingkaran, sedangkan luas juring adalah area yang dibatasi oleh busur dan dua jari-jari yang menghubungkannya ke pusat lingkaran.

Bagaimana cara menghitung panjang busur?

Panjang busur dapat dihitung dengan rumus: Panjang Busur = (Sudut Busur/360) x 2πr, di mana r adalah jari-jari lingkaran.

Apa rumus untuk menghitung luas juring?

Luas juring dapat dihitung dengan rumus: Luas Juring = (Sudut Busur/360) x πr², di mana r adalah jari-jari lingkaran.

Apa saja penerapan praktis dari panjang busur dan luas juring?

Panjang busur dan luas juring memiliki aplikasi dalam bidang arsitektur, teknik, desain, dan pembuatan peta.