Pembagian pecahan merupakan konsep matematika dasar yang sangat penting untuk dikuasai oleh siswa kelas 6. Konsep ini digunakan dalam berbagai aplikasi kehidupan sehari-hari, mulai dari memasak hingga perhitungan ilmiah. Dengan memahami prinsip-prinsip dasar pembagian pecahan, siswa dapat mengembangkan keterampilan pemecahan masalah yang lebih kuat dan mempersiapkan diri untuk topik matematika yang lebih kompleks.
Dalam artikel ini, kita akan mengeksplorasi konsep pecahan, jenis-jenis pecahan, dan langkah-langkah membagi pecahan. Kita juga akan membahas contoh soal pembagian pecahan, cara menyederhanakan hasil pembagian, dan aplikasi praktis pembagian pecahan dalam kehidupan sehari-hari.
Jenis-jenis Pecahan
Pecahan merupakan representasi bagian dari keseluruhan yang dibagi menjadi bagian-bagian yang sama. Terdapat beberapa jenis pecahan, antara lain:
Pecahan Biasa
Pecahan biasa ditulis dalam bentuk a/b, di mana a adalah pembilang (jumlah bagian yang diambil) dan b adalah penyebut (jumlah total bagian).
- Contoh: 1/2 (dibaca satu per dua) mewakili setengah dari suatu keseluruhan.
Pecahan Campuran
Pecahan campuran terdiri dari bilangan bulat dan pecahan biasa. Pecahan ini digunakan untuk mewakili jumlah yang lebih besar dari 1.
- Contoh: 2 1/2 (dibaca dua satu per dua) mewakili dua keseluruhan dan setengah dari keseluruhan.
Pecahan Desimal
Pecahan desimal adalah pecahan yang ditulis menggunakan titik desimal. Pecahan ini merupakan bentuk lain dari pecahan biasa, di mana penyebutnya adalah 10, 100, 1000, dan seterusnya.
- Contoh: 0,5 (dibaca nol koma lima) mewakili setengah dari suatu keseluruhan.
Operasi Pembagian Pecahan
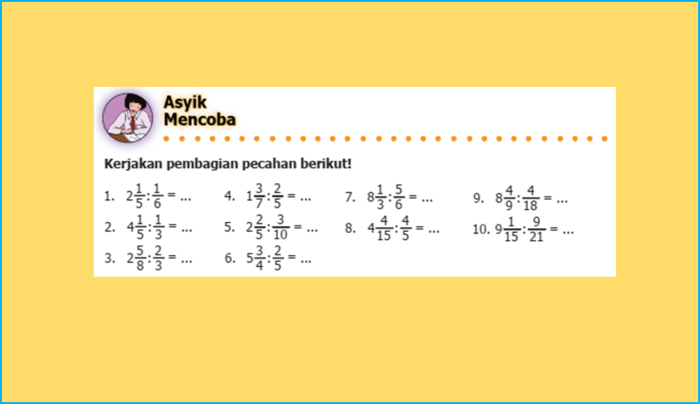
Pembagian pecahan adalah operasi matematika yang melibatkan pembagian satu pecahan dengan pecahan lainnya. Operasi ini digunakan untuk menyelesaikan berbagai masalah, seperti membagi jumlah tertentu ke dalam bagian-bagian yang sama atau membandingkan ukuran dua pecahan.
Langkah-Langkah Membagi Pecahan
- Balik pecahan pembagi (penyebut dan pembilangnya).
- Kalikan pecahan yang akan dibagi dengan pecahan pembagi yang telah dibalik.
- Sederhanakan pecahan hasil pembagian, jika memungkinkan.
Peran Pembilang dan Penyebut dalam Pembagian Pecahan
Dalam operasi pembagian pecahan, pembilang mewakili jumlah bagian yang dibagi, sedangkan penyebut mewakili jumlah bagian yang sama dalam keseluruhan. Pembagian pecahan menghasilkan pecahan baru yang menunjukkan bagian dari keseluruhan yang diperoleh setelah pembagian.
Contoh Soal Pembagian Pecahan
Pembagian pecahan adalah operasi matematika yang membagi nilai satu pecahan dengan pecahan lainnya. Berikut adalah beberapa contoh soal pembagian pecahan:
- Bagilah 1/2 dengan 1/4
- Temukan hasil bagi dari 3/5 dan 2/3
- Bagilah 7/8 dengan 1/2
- Hitung hasil bagi dari 5/6 dan 1/3
- Temukan hasil bagi dari 2/5 dan 3/4
Untuk menyelesaikan soal pembagian pecahan, kita dapat menggunakan aturan berikut:
- Balikkan pecahan pembagi (pecahan yang berada di bawah tanda bagi).
- Kalikan pecahan pembilang dengan pecahan pembagi yang telah dibalik.
Sebagai contoh, untuk membagi 1/2 dengan 1/4, kita akan membalik 1/4 menjadi 4/1 dan mengalikannya dengan 1/2:“`
/2 ÷ 1/4 = 1/2 x 4/1 = 4/2 = 2
“`
Cara Menyederhanakan Hasil Pembagian

Setelah melakukan pembagian pecahan, langkah selanjutnya adalah menyederhanakan hasilnya menjadi bentuk yang paling sederhana. Proses penyederhanaan ini dilakukan dengan mencari faktor persekutuan terbesar (FPB) dari pembilang dan penyebut hasil pembagian.
Menyederhanakan Hasil Pembagian Pecahan
- Cari FPB Pembilang dan Penyebut: Tentukan FPB dari pembilang dan penyebut hasil pembagian.
- Bagi Pembilang dan Penyebut dengan FPB: Bagilah pembilang dan penyebut hasil pembagian dengan FPB yang ditemukan.
- Hasilnya Adalah Pecahan Paling Sederhana: Hasil pembagian setelah disederhanakan adalah pecahan paling sederhana.
Contoh Penyederhanaan Hasil Pembagian Pecahan
Misalkan hasil pembagian pecahan adalah 12/18.
- Cari FPB: FPB dari 12 dan 18 adalah 6.
- Bagi Pembilang dan Penyebut: Bagilah 12 dan 18 dengan 6.
- Hasilnya: 12/18 = (12 ÷ 6)/(18 ÷ 6) = 2/3.
Jadi, hasil pembagian 12/18 setelah disederhanakan menjadi 2/3.
Aplikasi Pembagian Pecahan dalam Kehidupan Sehari-hari

Pembagian pecahan memiliki berbagai aplikasi dalam kehidupan sehari-hari, termasuk dalam memasak, pembagian harta warisan, dan perhitungan ilmiah.
Memasak
Dalam memasak, pembagian pecahan digunakan untuk mengukur bahan-bahan dengan tepat. Misalnya, jika resep membutuhkan 1/2 cangkir tepung dan Anda hanya memiliki 3/4 cangkir tepung, Anda dapat membagi 3/4 cangkir dengan 1/2 cangkir untuk menentukan jumlah tepung yang Anda perlukan.
Pembagian Harta Warisan
Dalam pembagian harta warisan, pembagian pecahan digunakan untuk mendistribusikan harta secara adil di antara ahli waris. Misalnya, jika sebuah warisan dibagi di antara tiga ahli waris, masing-masing akan menerima 1/3 dari warisan.
Perhitungan Ilmiah
Dalam perhitungan ilmiah, pembagian pecahan digunakan untuk menyelesaikan masalah yang melibatkan besaran fisika. Misalnya, jika sebuah benda bergerak dengan kecepatan 1/2 meter per detik dan bergerak selama 3 detik, jarak yang ditempuh benda tersebut dapat dihitung dengan membagi 1/2 meter per detik dengan 3 detik.
Kesimpulan

Memahami pembagian pecahan adalah kunci untuk membangun fondasi matematika yang kuat. Dengan menguasai konsep ini, siswa kelas 6 dapat mengembangkan keterampilan berpikir kritis, memecahkan masalah, dan menerapkan matematika dalam berbagai situasi kehidupan nyata. Dengan latihan dan pemahaman yang tepat, siswa dapat menguasai pembagian pecahan dan mempersiapkan diri untuk kesuksesan dalam matematika.
Jawaban untuk Pertanyaan Umum
Apa itu pecahan?
Pecahan adalah bagian dari keseluruhan.
Apa saja jenis-jenis pecahan?
Pecahan biasa, pecahan campuran, dan pecahan desimal.
Bagaimana cara membagi pecahan?
Dengan membalik pecahan pembagi dan mengalikannya dengan pecahan yang dibagi.
Bagaimana cara menyederhanakan hasil pembagian pecahan?
Dengan membagi pembilang dan penyebut dengan faktor persekutuan terbesar (FPB).
